ch10 降维与度量学习

降维的动机

从 k-近邻算法的角度看降维

如果给定测试样本\(x\)与最近邻样本\(z\)，那么正确率就为

\[P(acc) = P(c_1 = c_2 | x, z) = \sum_{c \in \mathcal{C}} P(c_1 = c_2 = c | x, z) = \sum_{c \in \mathcal{C}} P(c_1 = c | x) P(c_2 = c | z) \]

如果在度量空间中满足密采样假设（即在任意近的\(\delta\)距离内存在一个样本），那么可以认为\(P(c_1 = c | x) = P(c_2 = c | z)\)，即满足同分布的假设，那么

\[P(err) = 1 - P(acc) = 1 - \sum_{c \in \mathcal{C}} P(c_1 = c | x) P(c_2 = c | z) \\ \approx 1 - \sum_{c \in \mathcal{C}} P(c_1 = c | x)^2 \\ \leq 1 - P(c_1 = c^* | x)^2 \\ \leq 2 \times (1 - P(c_1 = c^* | x)) \]

可以发现，KNN 的效果至少与贝叶斯最优分类器的一半好，但事实并非如此，最主要的原因就是维度灾难，即在高维空间中密采样假设不成立，因此需要降维。

从高维空间的角度看降维

我们假设数据在归一化后的立方体内均匀分布，那么在高维空间中，大部分数据点都会集中在立方体的角落，而在中心附近的数据点却很少，这就是维度灾难的原因。

即在高维空间中，满足密采样需要的样本个数很多，数据分布稀疏，因此为了缓解维度灾难，一种手段就是降维。

低维嵌入——MDS

降维即通过数学变换将高维数据映射到一个低维子空间

能够进行降维的原因是，与任务相关的信息通常只占据了高维空间的一个低维子空间

而一种古老的想法（当然也很有用），就是保持样本点之间的距离关系，即多维尺度缩放，这种方法称为多维尺度分析（MDS）

我们定义原先的数据矩阵为\(B \in \mathbb{R}^{m \times d}\), 降维后的数据矩阵为\(Z \in \mathbb{R}^{m \times d'}\), \(d' < d\)，我们要对距离矩阵\(D \in \mathbb{R}^{m \times m}\)，同时根据书上的变换可以得到内积矩阵与距离矩阵的关系，即内积矩阵与距离矩阵之间可以相互转换，因此我们可以通过内积矩阵来进行降维。

降维前的内积矩阵为

\[B B^T \]

我们想要获得如下的关系式

\[B B^T \approx Z Z^T \]

我们可以通过谱分解来获得\(Z\)，即

\[B B^T = U \Sigma U^T \\ B B^T = \sum_{i=1}^d \sigma_i u_i u_i^T \]

我们丢弃掉\(\sigma_i\)较小的部分(低秩矩阵近似)，即只保留前\(d'\)个，即

\[Z Z^T = \sum_{i=1}^{d'} \sigma_i u_i u_i^T \\ Z = U_{d'} \Sigma_{d'}^{1/2} \]

那么就可以获得与原始数据矩阵\(B\)相近的降维后的数据矩阵\(Z\)。

线性降维

一般来说，获得低维嵌入的方法是对原始的样本点进行线性变换，即

\[z = W^T x \]

其中\(W \in \mathbb{R}^{d \times d'}\)，\(d'\)为降维后的维度。

一般而言，\(W\)满足各个列向量（即降维后的坐标系）的正交性，同时认为在原先的空间中，\(W\)是一组正交基，即

\[x = \sum_{i=1}^d z_i w_i \\ \Rightarrow z_i = w_i^T x \]

而在降维后的空间中，选取部分基，即只选取前\(d'\)个基，即

\[z = W^T x \]

而对于基的选取，有多种方式，如 PCA、LDA 等。

对于 PCA，一般我们希望在降维后的空间中，样本点之间的方差最大/重构误差最小

样本点方差最大

我们假设原始数据矩阵为\(X \in \mathbb{R}^{m \times d}\)，已经被中心化，即\(\sum_{i=1}^m x_i = 0\)，那么我们希望在降维后的空间中，样本点之间的方差最大，即

\[\max_W \text{tr}(W^T X^T X W) \\ \text{s.t.} W^T W = I \]

注：这里的 \(X^T X\) 为协方差矩阵，内积要对应的是特征维度向量的内积

求解上述问题，可以通过拉格朗日乘子法，即

\[\mathcal{L} = \text{tr}(W^T X^T X W) - \text{tr}(\Lambda (W^T W - I)) \]

可以认为化简为

\[\max_W \sum_{i=1}^{d'} w_i^T X^T X w_i \\ \text{s.t.} w_i^T w_i = 1, i = 1, 2, \cdots, d' \]

重构误差最小

我们希望在降维后的空间中，样本点之间的重构误差最小，即\(\min \| x_i - W z \|_2^2\)，其中\(z = W^T x_i\)，即

\[\min_W \sum_{i=1}^m \| x_i - W W^T x_i \|_2^2 \\ \Rightarrow \min_W \sum_{i=1}^m ( x_i - W W^T x_i )^T ( x_i - W W^T x_i ) \\ \Rightarrow \min_W \sum_{i=1}^m x_i^T x_i - x_i^T W W^T x_i \\ \Rightarrow \max_W \sum_{i=1}^m x_i^T W W^T x_i \\ \]

那么就等价于样本点方差最大的问题（这里的推导将 x 看作列向量）

求解上述问题，可以通过拉格朗日乘子法，即最终得到

\[X^T X w_i = \lambda_i w_i \]

那么方差即为

\[w_i^T X^T X w_i = \lambda_i \]

于是优化目标可以化为

\[\max_W \sum_{i=1}^{d'} \lambda_i \]

即我们选择前\(d'\)个特征值对应的特征向量作为\(W\)。

非线性降维

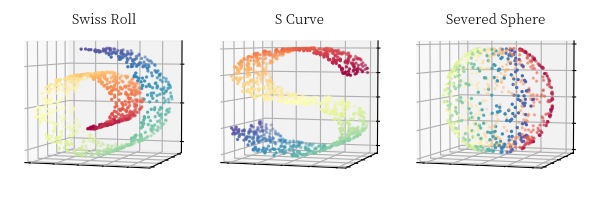
线性降维假设数据到低维空间的映射是线性的，然而在实际任务中，可能需要非线性的映射才能获得低维嵌入

Kernel PCA

先将样本通过核函数映射到高维空间，然后再进行 PCA

最核心的行为就是协方差矩阵可以化为(\(X \in \mathbb{R}^{m \times d}\))

\[cov(X, X) = X^T X = \sum_{i=1}^m x_i x_i^T \]

那么优化行为可以通过如下的式子进行

\[\sum_{i=1}^m \phi(x_i) \phi(x_i)^T w_j = \lambda_j w_j \\ \iff \phi(X) \phi(X)^T w_j = \lambda_j w_j \]

得到\(w_j\)的关于坐标的表达式

\[w_j = \sum_{i=1}^m \alpha_{ij} \phi(x_i) = \phi(X) \alpha_j \]

ISOMAP

ISOMAP 是一种基于流形学习的降维方法，即认为数据点分布在一个低维流形上，而不是在高维空间中，即在局部具有欧氏空间的性质，而在全局具有非欧性质

而 manifold learning 的核心就是找到数据点之间的距离，即找到数据点之间的最短路径（测地线），即 ISOMAP 的核心就是找到数据点之间的最短路径，通过 dijkstra 算法来求解

随后使用 MDS 来进行降维

LLE

LLE 是一种基于局部线性关系的降维方法，即认为数据点之间的关系是局部线性的

LLE 的核心就是找到数据点之间的局部线性关系，即找到数据点之间的权重，类似于 word2vec 中的 skip-gram 模型

随后将所有的数据点映射到低维空间中，通过最小化重构误差来求解

度量学习

降维的目的就是找到一个低维嵌入，使得低维空间的学习性能变得更好

事实上每一个空间都对应了样本属性上的一个距离度量，找到一个好的低维嵌入就是找到一个好的距离度量

因此可以针对这样的想法，直接对距离度量进行学习，即度量学习（metric learning）

而为了度量学习，我们需要定义一个参数化的距离函数，即 mahalanobis 距离

\[d(x, y) = (x - y)^T M (x - y) \]

而距离要满足一些性质，如非负性、对称性、三角不等式等，因此\(M\)需要满足一些约束条件

• 非负性：\(M \succeq 0\)
• 对称性：\(M = M^T\)
• 同一性：\(d(x,y) = 0 \iff x = y\)
• 三角不等式：\(d(x, y) \leq d(x, z) + d(z, y)\)

为了之后问题的方便，我们可以将\(M\)写成\(M = PP^T\)的形式(\(M = S \sqrt{\Lambda} S^T S \sqrt{\Lambda} S^T\))

学习度量需要设定一个目标函数，这里以最近邻分类器为例，即

\[\min_P 1 - \sum_{i=1}^m \sum_{j \in \Omega_i} \frac{\exp(- \| P^T x_i - P^T x_j\|_2^2)}{\sum_l \exp(- \| P^T x_i - P^T x_l\|_2^2)} \]

即将距离转化为概率，认为相同类的样本点距离越近越好，不同类的样本点距离越远越好