ch3 不确定性和风险
重点
- 阿莱悖论(独立性)
- 冯诺依曼公式
关键
了解奈特关于不确定性的研究及其基本结论;
了解行为经济学对时间不确定性的分析,知道“双曲贴现”的概念并运用该理论解释相关的经济现象;
熟悉期望效用理论,并能运用期望效用函数测度风险,
掌握风险升水等重要概念。
不确定性
- 可能来源于内生性:与人有关的因素
- 外生性: 与人无关的环境因素
双曲线贴现:
与强化学习中的奖励(Reward)和回报(Return)类似
定义:人们在小的盈利相对于大的盈利来得快的情况下会偏好小的盈利,在大小盈利的实现时间都很长且两个时间相近的情况下,人们又会偏好大的盈利的趋向
结论:贴现率随着时间显著的下降,但是未来的偏好却总是根据不断变化的现在的时点。个体依采用的贴现率在两期之间作权衡,贴现率低就偏爱近期;贴现率高则偏爱远期
不确定性与期望效用理论(如何应对不确定性)
期望效用理论
不确定性的度量:期望效用理论(EU)
如果知道对时间的时候概率的排序,并以此作为事前决策的依据的过程
- 不确定
- 事后概率已知
单赌
对事件的 n 种可能的结果乘以对应的概率
复赌
将奖品本身又进行赌博本身的赌博。
- 赌徒在赌场能用 100 元赢得 100 万的概率有多少
风险与不确定
不确定性(uncertainty):不确定性是指不能肯定某种事件是否会发生,也不知道其发生的概率。
风险(risk):风险则指虽然不能肯定某种事件是否会发生,但知道其发生的概率
联想:统计学习借用的期望风险和经验风险函数
冯诺依曼——摩根斯坦(VNM)函数
函数的定义又在效用的偏序关系上定义了连续性+独立性
-
完备性:对于任意两个结果 和 ,决策者能够比较并得出 $ A \succ B A \prec B A \sim B $ 之一,即决策者能够对所有结果进行排序。
-
传递性:如果 且 ,则 。
-
连续性:如果 ,则存在一个概率 使得决策者对 的偏好与一个混合彩票 等价,即 。
-
独立性:如果 ,则对于任意 和 ,有 。
根据这些公理,可以证明存在一个函数 ,称为 VNM 效用函数,使得对于任意两个结果 和 ,有 当且仅当 。
具体来说,VNM 效用函数 满足以下条件:
- 对于确定性结果 和 ,如果 ,则 。
- 对于一个混合彩票 ,效用为 。
期望效用悖论
阿莱悖论:对于不确定性的情况,人们的选择并不总是遵循期望效用理论
不确定条件下依旧拥有 5 个选择公理(加上不相等公理)


风险与风险度量
风险:通常以实际结果与人们对该结果的期望值之间的离差(deviations)来度量某一事件的风险程度的大小
通常风险以方差来度量
风险态度
对于一个函数来说,我们通常由凹凸的定义,而对于两点之间的组合,可以用一条直线来表示,曲线代表确定的效用,直线代表不确定的效用
即我们希望比较混合彩票期望收益的效用与期望效用之间的关系,即
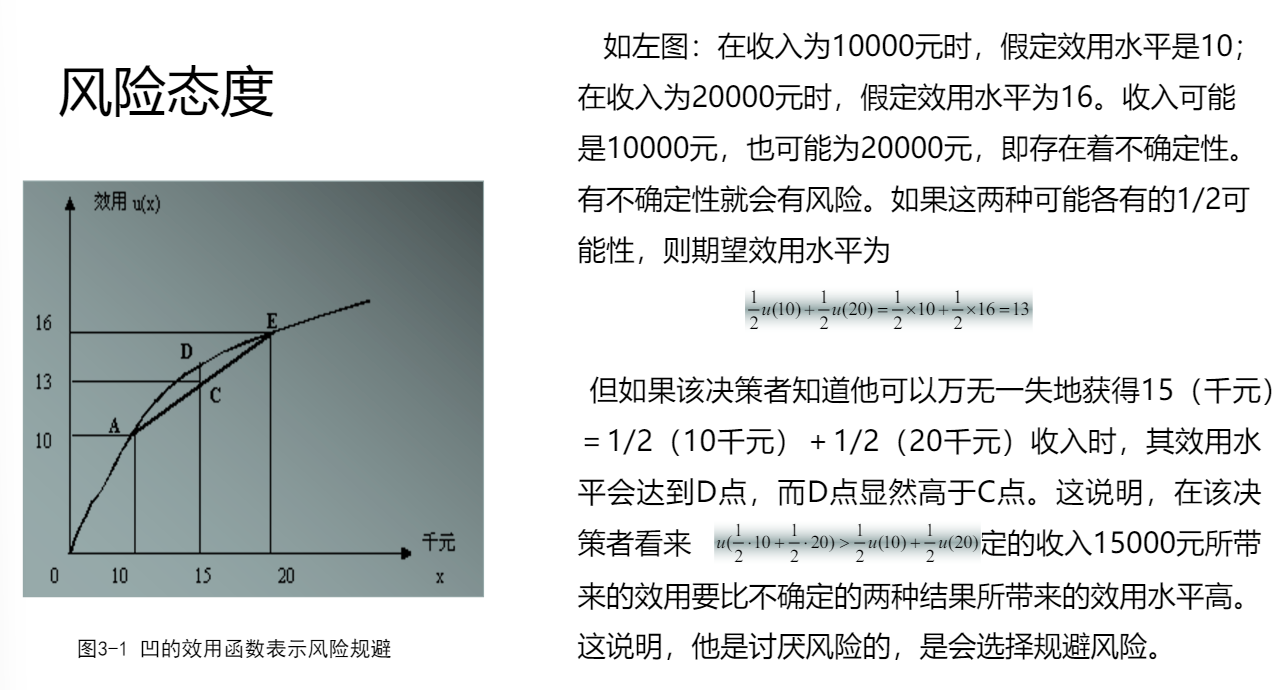
convex function 的效用函数对应的风险态度是风险规避的,concave function 的效用函数对应的风险态度是风险爱好的
affine function 的效用函数对应的风险态度是风险中立的
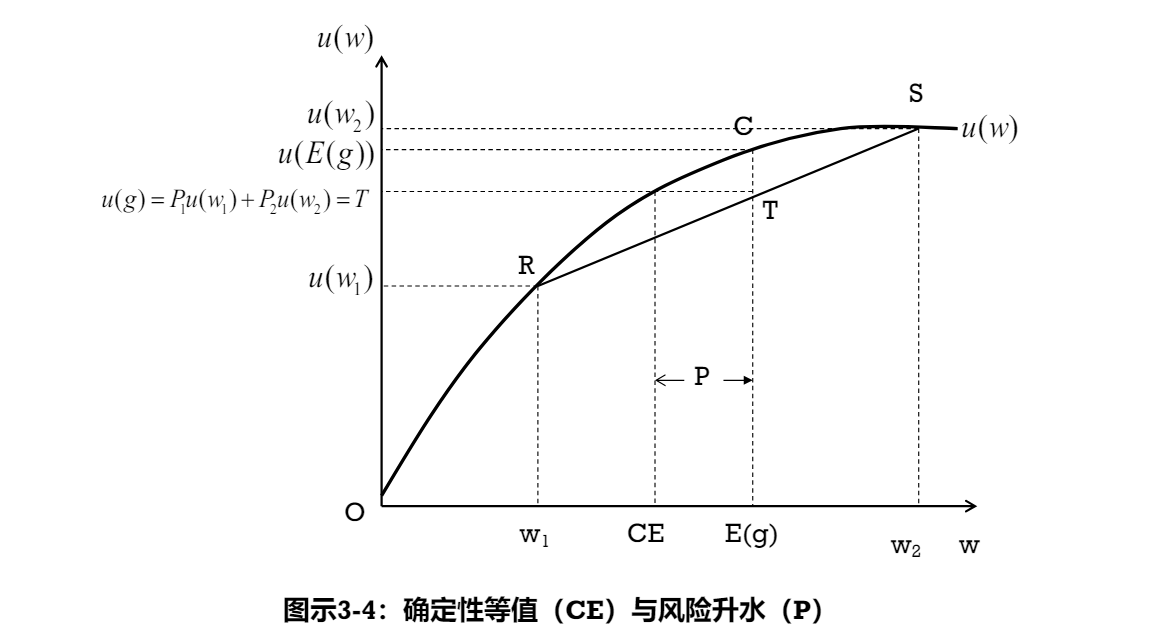
确定性等值 CE、风险升水
确定性等值(certainty equivalent):在不确定性条件下,能够使个体在效用上感到满意的确定性收入
风险升水(risk premium):个体愿意为了避免风险而愿意放弃的一部分收入
投资组合
-
无风险资产
能够保证投资者获得固定的投资回报率 -
风险资产
收益率不确定,但是有一个期望收益率
通常,所以人们会把一定比例的财产投资于风险财产
如果假设投资者投资风险资产的比例为,那么预期收益率是一个线性组合
这个投资组合的风险可以使用该投资组合的方差表示
例题
期望效用例题

在此例中,虽然混合情景的期望值为 5.2 元,消费者却只赋予其与 4 元相同的效用(0.6),表明消费者对不确定性情景存在风险规避行为。其中的差值可以定义为风险升水


保险定价例题

若不参保,则根据期望效用值与确定性等价的确定性收入相同,可以计算得出
那么消费者能够接受的最大保费为
如果保险公司全额赔付,那么保险公司的个人支出为
那么保险公司的净收益为
投资组合例题
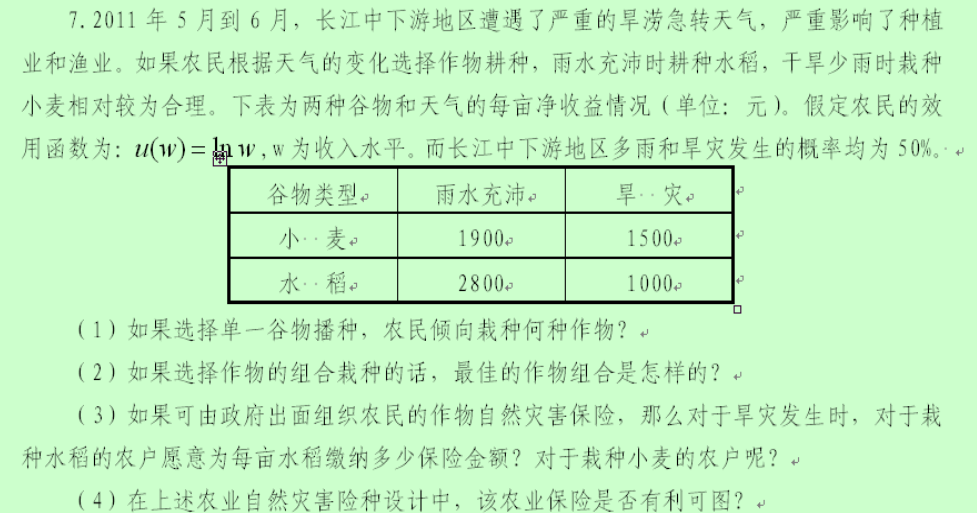
1
2
假设投资者投资小麦的比例为,那么预期收益率是一个线性组合
那么求解 b 是一个优化问题
3
依旧是一个保险定价问题,我们在此题只考虑小麦以及赔付旱灾与雨水充沛之间的差值
如果保险商全赔,那么能够接受的最大保费为
4
如果全赔,无利可图,具体解法见上一题



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!