RL Introduction

参考

动手学强化学习
drl

MDP

Markov Decision Process 是一个五元组\(<S, A, T, R, \gamma>\)，是强化学习概念的起源，其中：

• \(S\) 是状态空间
• \(A\) 是动作空间
• \(T: S \times A \times S \to \mathbb{R}\) 是状态转移概率，\(T(s, a, s')\) 表示在状态\(s\)下采取动作\(a\)转移到状态\(s'\)的概率，即\(P(s' | s, a)\)
• \(R: S \times A \times S \to \mathbb{R}\) 是奖励函数，\(R(s, a, s')\) 表示在状态\(s\)下采取动作\(a\)转移到状态\(s'\)的奖励，强化学习的性能取决于奖励的设定
• \(\gamma\) 是折扣因子，用于平衡当前奖励和未来奖励的重要性

MDP 的目标是找到一个策略\(\pi: S \to A\)，策略可以是确定或随机的，一般随机（即\(\pi(a | s)\)），使得在这个策略下，能够最大化期望回报（Return），注意，是一个随机过程，因此我们需要考虑期望回报

我们在与环境交互的过程中，会获得一系列的状态、动作、奖励的序列，我们可以得到轨迹 trajectory

\[s_1, a_1, r_1, s_2, a_2, r_2, \dots, s_T \]

我们考虑效用函数，以\(\gamma\)为贴现率，定义 t 时刻的回报

\[U_t = R_{t+1} + \gamma R_{t+2} + \dots = \sum_{k=0}^{\infty} \gamma^k R_{t+k} = R_{t+1} + \gamma U_{t+1} \]

我们发现\(U_t\)实际上是一个随机变量，因为\(t\)时刻之后的奖励\(R_t\)是未知的，它依赖于\(s_{t}, a, s_{t+1}\), 即\(R(s, a, s')\)

那么为了评估当前的形势，我们需要考虑期望回报，有固定的策略\(\pi\)，我们可以得到动作价值函数

\[Q_\pi(s, a) = \mathbb{E}[U_t | S_t = s, A_t = a] \]

消去策略的影响，我们可以得到最优动作价值函数

\[Q^*(s, a) = \max_\pi Q_\pi(s, a) \]

那么也可以有状态价值函数

\[V_\pi(s) = \mathbb{E}[U_t | S_t = s] = \sum_{a} \pi(a|s) Q_\pi(s, a) (\text{全期望公式}) \]

Bellman Equation:(如何推导？)

\[Q(s, a) = \mathbb{E}_{S_{t+1}:,A_{t+1}:}[U_t| S_t = s, A_t = a] = \sum_{s'} T(s, a, s') [R(s, a, s') + \gamma V(s')] \]

\[V(s) = \mathbb{E}[U_t|S_t = s] = \sum_{a} \pi(a|s) \sum_{s'} T(s, a, s') [R(s, a, s') + \gamma V(s')] \]

Bellman Optimality Equation:

\[Q^*(s, a) = \sum_{s'} T(s, a, s') [R(s, a, s') + \gamma V^*(s')] \]

\[V^*(s) = \max_a \sum_{s'} T(s, a, s') [R(s, a, s') + \gamma V^*(s')] \]

于是我们可以推导出最优方程的形式：

\[Q^*(s, a) = R(s, a) + \gamma \sum_{s'} T(s, a, s') \max_{a'} Q^*(s', a') \]

\[V^*(s) = \max_a Q^*(s, a) \]

动态规划算法

而在回报和状态转移概率都是已知的情况下，即有模型的情况下，我们可以有多种求解方法：

Value Iteration

我们对状态价值函数进行迭代更新，直到收敛，我们可以得到最优的状态价值函数，然后通过最优状态价值函数得到最优策略

根据 Bellman 最优方程，我们可以得到如下的公式：

\[V^*(s) = \max_a \sum_{s'} T(s, a, s') [R(s, a, s') + \gamma V^*(s')] = \max_a Q^*(s, a) \]

可以将其写成迭代更新的方式

\[V_{k+1}(s) = \max_a \sum_{s'} T(s, a, s') [R(s, a, s') + \gamma V_k(s')] = \max_a Q_k(s, a) \]

依据如上的等式，在一次迭代的时候遍历所有的状态，找出每一个状态对应的最大估计 Q 值，然后更新 V 值，直到收敛。最终的不动点对应着最优的 V 值，每一个状态对应的最优动作可以通过最大化 Q 值得到

def value_iteration(env:GridWorld, gamma=0.9, theta=1e-6):
    """
    Value iteration algorithm for solving a given environment.
    ...
    """
    # initialize the value function and policy
    V = np.zeros((env.size, env.size))
    policy = np.zeros((env.size, env.size), dtype=int)
    ####
    # Implement the value iteration algorithm here

    iterations = 0

    while True:
        updated_V = V.copy()

        iterations += 1

        for now_state_x in range(env.size):
            for now_state_y in range(env.size):
                Q_values = []
                env.state = (now_state_x, now_state_y)

                for action in range(4):

                    # get s' and reward
                    next_state, reward = env.step(action=action)

                    next_state_x, next_state_y = next_state

                    # calc Q_value
                    Q_value = reward + gamma * V[next_state_x, next_state_y]

                    Q_values.append(Q_value)

                    # reset now_state
                    env.state = (now_state_x, now_state_y)

                # find max Q
                max_Q = max(Q_values)

                updated_V[now_state_x, now_state_y] = max_Q
                policy[now_state_x, now_state_y] = Q_values.index(max_Q)

        if np.amax(np.fabs(updated_V - V)) <= theta:
            print ('Value-iteration converged at iteration# %d.' %(iterations))
            break
        else:
            V = updated_V
    ####

    env.reset()
    return policy

最终结果如下

Value-iteration converged at iteration# 154.
↓ → ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
↓ ↓ → ↓ ↓ ↓ ↓ ↓ ↓ ↓
↓ ↓ ↓ → ↓ ↓ ↓ ↓ ↓ ↓
↓ ↓ ↓ ↓ → ↓ ↓ ↓ ↓ ↓
↓ ↓ ↓ ↓ ↓ → ↓ ↓ ↓ ↓
↓ ↓ ↓ ↓ ↓ ↓ → ↓ ↓ ↓
↓ ↓ ↓ ↓ ↓ ↓ ↓ → ↓ ↓
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ → ↓
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
→ → → → → → → → → ↓

========== SHOW PATH ==========
(0, 0) -> (1, 0) -> (2, 0) -> (3, 0) -> (4, 0) ->
(5, 0) -> (6, 0) -> (7, 0) -> (8, 0) -> (9, 0) ->
(9, 1) -> (9, 2) -> (9, 3) -> (9, 4) -> (9, 5) ->
(9, 6) -> (9, 7) -> (9, 8) -> (9, 9)
========== END  PATH ==========

Policy Iteration

从一个初始化的策略出发，先对当前的策略进行策略评估，然后改进策略，评估改进的策略，再进一步改进策略，经过不断迭代更新，直到策略收敛，这种算法被称为“策略迭代”

• Policy Evaluation

根据 Bellman 期望方程，我们可以得到如下的公式：

\[V_{k+1}(s) = \sum_{a} \pi(a|s) \sum_{s'} T(s, a, s') [R(s, a, s') + \gamma V_k(s')] \]

我们可以知道\(V^k =V^\pi\)是一个不动点

当迭代到收敛时，我们可以得到这个策略下的状态值函数

def policy_evaluation(policy:np.ndarray, env:GridWorld, gamma=0.9, theta=1e-6):
    """
    Evaluate a policy given an environment.
    ...
    """
    V = np.zeros((env.size, env.size))
    ####
    # Implement the policy evaluation algorithm here

    iterations = 0

    while True:

        iterations += 1

        updated_V = V.copy()

        for now_state_x in range(env.size):
            for now_state_y in range(env.size):

                env.state = (now_state_x, now_state_y)

                action = policy[now_state_x, now_state_y]

                next_state, reward = env.step(action=action)

                updated_V[now_state_x, now_state_y] = reward + gamma * V[next_state[0], next_state[1]]

        if np.amax(np.fabs(updated_V - V)) <= theta:
            V = updated_V
            print ('Policy-evaluation converged at iteration# %d.' %(iterations))
            break
        else:
            V = updated_V

    ####

    return V

• Policy Improvement

假设我们在原来的状态价值函数的基础上，对于每一个状态，我们能够找到一个更优的动作\(a\), 使得\(Q^\pi (s, a) \geq V^\pi(s)\)，那么能够获得更高的回报

现在如果我们能够找到一个新的策略\(\pi'\)，使得\(V^{\pi'}(s) \geq V^\pi(s)\)，那么我们就可以得到一个更好的策略

因此我们可以贪心的选择每一个状态动作价值最大的那个动作，也就是\(\max V\)

\[\pi'(s) = \arg \max_a Q^\pi(s, a) = \arg \max_a \sum_{s'} T(s, a, s') [R(s, a, s') + \gamma V^\pi(s')] \]

def policy_iteration(env:GridWorld, gamma=0.9, theta=1e-6):
    """
    Perform policy iteration to find the optimal policy for a given environment.
    ...
    """
    policy = np.zeros((env.size, env.size), dtype=int)

    ####
    # Implement the policy iteration algorithm here

    iterations = 0

    while True:

        iterations += 1

        V = policy_evaluation(policy=policy, env=env)

        policy_stable = True

        for now_state_x in range(env.size):
            for now_state_y in range(env.size):
                Q_values = []
                env.state = (now_state_x, now_state_y)

                for action in range(4):

                    # get s' and reward
                    next_state, reward = env.step(action=action)

                    next_state_x, next_state_y = next_state

                    # calc Q_value
                    Q_value = reward + gamma * V[next_state_x, next_state_y]

                    Q_values.append(Q_value)

                    # reset now_state
                    env.state = (now_state_x, now_state_y)

                # update policy
                max_Q = max(Q_values)
                now_action = policy[now_state_x, now_state_y]
                new_action = Q_values.index(max_Q)

                if now_action != new_action:
                    policy_stable = False
                    policy[now_state_x, now_state_y] = Q_values.index(max_Q)

        if policy_stable:
            print ('Policy-iteration converged at iteration# %d.' %(iterations))
            break

    ####
    env.reset()
    return policy

最终结果如下

Policy-evaluation converged at iteration# 133.
Policy-evaluation converged at iteration# 154.
Policy-evaluation converged at iteration# 154.
Policy-evaluation converged at iteration# 154.
Policy-evaluation converged at iteration# 154.
Policy-evaluation converged at iteration# 154.
Policy-evaluation converged at iteration# 154.
Policy-evaluation converged at iteration# 154.
Policy-evaluation converged at iteration# 154.
Policy-evaluation converged at iteration# 154.
Policy-evaluation converged at iteration# 154.
Policy-evaluation converged at iteration# 154.
Policy-evaluation converged at iteration# 154.
Policy-evaluation converged at iteration# 154.
Policy-evaluation converged at iteration# 154.
Policy-evaluation converged at iteration# 154.
Policy-evaluation converged at iteration# 154.
Policy-evaluation converged at iteration# 154.
Policy-evaluation converged at iteration# 154.
Policy-iteration converged at iteration# 19.
↓ → ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
↓ ↓ → ↓ ↓ ↓ ↓ ↓ ↓ ↓
↓ ↓ ↓ → ↓ ↓ ↓ ↓ ↓ ↓
↓ ↓ ↓ ↓ → ↓ ↓ ↓ ↓ ↓
↓ ↓ ↓ ↓ ↓ → ↓ ↓ ↓ ↓
↓ ↓ ↓ ↓ ↓ ↓ → ↓ ↓ ↓
↓ ↓ ↓ ↓ ↓ ↓ ↓ → ↓ ↓
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ → ↓
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
→ → → → → → → → → ↓

========== SHOW PATH ==========
(0, 0) -> (1, 0) -> (2, 0) -> (3, 0) -> (4, 0) ->
(5, 0) -> (6, 0) -> (7, 0) -> (8, 0) -> (9, 0) ->
(9, 1) -> (9, 2) -> (9, 3) -> (9, 4) -> (9, 5) ->
(9, 6) -> (9, 7) -> (9, 8) -> (9, 9)
========== END  PATH ==========

Temporal Difference Learning

在实际的环境中，我们往往无法得到完整的环境信息，即我们无法得到状态转移概率和奖励函数，我们只能通过与环境的交互来得到这些信息，称为无模型学习

在蒙特卡洛方法中，我们需要等到一个 episode 结束后，才能更新状态价值函数，而在 TD 方法中，我们可以在每一步更新状态价值函数

即在蒙特卡洛方法中，获取期望回报的公式为

\[V^\pi(s_t) = \mathbb{E}[G_t | S_t = s_t] = \frac{1}{N} \sum_{i=1}^{N} G_t \]

增量更新公式为

\[V(s_t) = V(s_t) + \alpha [G_t - V(s_t)] \]

而在 TD 方法中，更新状态价值函数的公式为

\[V(s_t) = V(s_t) + \alpha [r_t + \gamma V(s_{t+1}) - V(s_t)] \]

这是因为通过单步采样，我们可以得到\(r_t\)和\(s_{t+1}\)，而在蒙特卡洛方法中，我们需要等到 episode 结束后才能得到\(G_t\)，而 TD 可以直接估计\(G_t\)

State-Action-Reward-State-Action (SARSA)

一个表格由所有状态和动作组成，表格中的 Q-value 表示在某个状态下采取某个动作的价值，我们可以通过不断的更新这个表格来得到最优的策略

这个表格的值由策略决定，策略变化，表格的值也会变化

\[Q^\pi(s_t, a_t) = \mathbb{E}[R_{t} + \gamma \max_{a} Q^\pi(s_{t+1}, a_{t+1}) | S_t = s_t, A_t = a_t] \]

那么左右两边都是可以计算的，并且都是对 Q 值的估计，我们可以通过不断的迭代来更新这个表格

即使用观测到的\(r_t\), \(s_{t+1}\) 以及通过最优策略抽样的出的\(a_{t+1}\)，得到\(r_t + \gamma q(s_{t+1}, a_{t+1})\)

采用 TD 的思想，将\(q(s_t, a_t) = (1-\alpha) q(s_t, a_t) + \alpha r_t + \alpha\gamma q(s_{t+1}, a_{t+1})\)

SARSA 用到了五元组\((s_t, a_t, r_t, s_{t+1}, a_{t+1})\)，因此我们可以通过不断的迭代来更新这个表格

在采样最佳策略的时候，使用\(\epsilon\)-greedy 策略，即以\(\epsilon\)的概率随机选择动作，以\(1-\epsilon\)的概率选择最优动作

请注意，抽样\(a_t, a_{t+1}\)均要使用\(\epsilon\)-greedy 策略

\[a = \begin{cases} \text{random action} & \text{with probability } \epsilon \\ \arg \max_a Q(s, a) & \text{with probability } 1-\epsilon \end{cases} \]

def extract_policy(q_table):
    """
    Extract the optimal policy from the Q-value table.
    ...
    """

    ####
    # Implement the function to extract the optimal policy from the Q-value table

    policy = np.argmax(q_table, axis=2)

    ####

    return policy

def sarsa(env:GridWorld, episodes=1000, alpha=0.1, gamma=0.9, epsilon=0.1):
    """
    SARSA algorithm for training an agent in a given environment.
    ...
    """
    q_table = np.zeros((env.size, env.size, 4))

    ####
    # Implement the SARSA algorithm here

    import random

    return_list = []

    for _ in range(episodes):

        x, y = env.start
        policy = extract_policy(q_table=q_table)
        action = policy[x, y]
        # 抽样
        if random.uniform(0, 1) <= epsilon:
                action = random.randint(0, 3)

        episode_return = 0

        while True:
            policy = extract_policy(q_table=q_table)

            env.state = (x, y)
            new_state, reward = env.step(action=action)

            episode_return += reward

            new_action = policy[new_state[0], new_state[1]]

            if random.uniform(0, 1) <= epsilon:
                new_action = random.randint(0, 3)

            q_table[x, y, action] += alpha * (reward + gamma * q_table[new_state[0], new_state[1], new_action] - q_table[x, y, action])

            x, y = new_state
            action = new_action

            if new_state == (9, 9):
                break

        return_list.append(episode_return)
    ####

    # plot the return
    import matplotlib.pyplot as plt
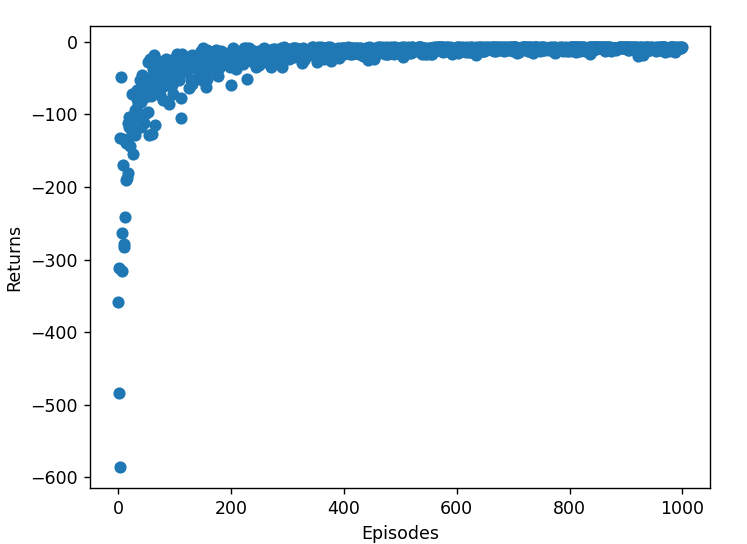
    plt.scatter(range(episodes), return_list)
    plt.xlabel('Episodes')
    plt.ylabel('Returns')
    plt.show()

    env.reset()
    return q_table

最终实验结果如下

↓ → ↓ ↓ → → → ↓ ↓ ←
↓ ↑ → → ↓ ↓ → ↓ ↓ ↓
→ ↓ ↑ → → → ↓ → ↓ ↓
↓ ↓ ↓ ↑ → → ↓ → ↓ ↓
↓ ↓ ↓ ↓ ↑ → → → → ↓
→ ↓ ↓ ↓ ↓ ↑ → → → ↓
→ → → ↓ ↓ ↓ ↑ → → ↓
→ → → → ↓ ↓ ↓ ↑ → ↓
→ → → → ↓ → ↓ ↓ ↑ ↓
→ → → → → → → → → ↑

========== SHOW PATH ==========
(0, 0) -> (1, 0) -> (2, 0) -> (2, 1) -> (3, 1) ->
(4, 1) -> (5, 1) -> (6, 1) -> (6, 2) -> (6, 3) ->
(7, 3) -> (7, 4) -> (8, 4) -> (9, 4) -> (9, 5) ->
(9, 6) -> (9, 7) -> (9, 8) -> (9, 9)
========== END  PATH ==========

Q-Learning

Q-Learning 是一种无模型的学习方法，它不需要环境的转移概率，只需要环境的奖励即可

基于 TD 的思想，我们可以通过不断的迭代来更新 Q 值

\[Q^*(s_t, a_t) = \mathbb{E}[r_t + \gamma \max_{a'} Q^*(s_{t+1}, a') | S_t = s_t, A_t = a_t] \]

\[Q(s_t, a_t) = (1-\alpha) Q(s_t, a_t) + \alpha [r_t + \gamma \max_{a'} Q(s_{t+1}, a')] \]

与 SARSA 类似，我们先通过\(\epsilon\)-greedy 策略抽样，然后更新 Q 值

def q_learning(env:GridWorld, episodes=1000, alpha=0.1, gamma=0.9, epsilon=0.1):
    """
    Q-learning algorithm for training an agent in a given environment.
    ...
    """
    q_table = np.zeros((env.size, env.size, 4))
    ####
    # Implement the Q-learning algorithm here

    return_list = []

    for _ in range(episodes):
        x, y = env.start

        episode_return = 0

        while True:
            policy = extract_policy(q_table=q_table)
            action = policy[x, y]

            if random.uniform(0,1) <= epsilon:
                action = random.randint(0,3)

            env.state = (x, y)
            new_state, reward = env.step(action=action)

            episode_return += reward

            q_table[x, y, action] += alpha * (reward + gamma *
                                              np.amax(q_table[new_state[0], new_state[1]]) - q_table[x, y, action])

            x, y = new_state

            if new_state == env.goal:
                break

        return_list.append(episode_return)
    ####

    import matplotlib.pyplot as plt
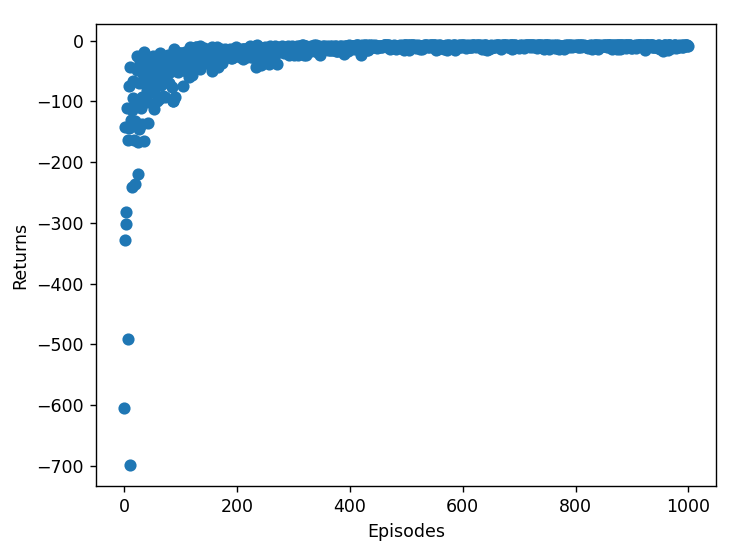
    plt.scatter(range(episodes), return_list)
    plt.xlabel('Episodes')
    plt.ylabel('Returns')
    plt.show()

    env.reset()
    return q_table

最终实验结果如下：

→ → → → → ↓ ↓ → ↓ ↑
↓ ↑ → → → ↓ ↓ ↓ ↓ ↓
↓ ↓ ↑ → → → ↓ ↓ ↓ ↓
↓ ↓ ↓ ↑ → → ↓ ↓ ↓ ↓
↓ ↓ ↓ ↓ ↑ → → → ↓ ↓
→ → → ↓ ↓ ↑ → → → ↓
→ → → → ↓ ↓ ↑ → → ↓
→ → → → ↓ ↓ ↓ ↑ → ↓
↑ → → → ↓ ↓ ↓ ↓ ↑ ↓
→ → → → → → → → → ↑

========== SHOW PATH ==========
(0, 0) -> (0, 1) -> (0, 2) -> (0, 3) -> (0, 4) ->
(0, 5) -> (1, 5) -> (2, 5) -> (2, 6) -> (3, 6) ->
(4, 6) -> (4, 7) -> (4, 8) -> (5, 8) -> (5, 9) ->
(6, 9) -> (7, 9) -> (8, 9) -> (9, 9)
========== END  PATH ==========