SVM

idea of SVM

分类问题的简化

首先我们考虑这样一个分类问题

• 二分类
• 线性分类边界
• 100% 可分

我们就能够考虑想出一个好的 idea，如下图所示

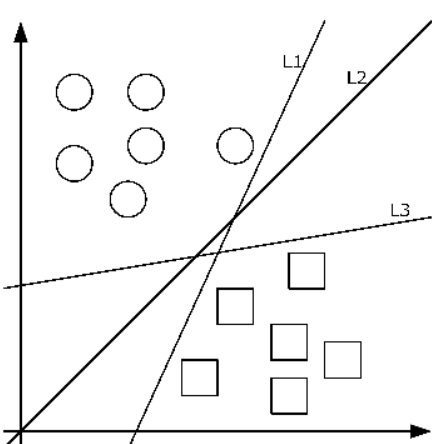
在上述条件满足的情况下，哪一个分类边界最好？

idea：最大化所有点到分类边界的最小距离，这个最小距离称为 margin。

形式化距离

函数间隔：\(| w^Tx_i + b |\)

几何间隔：\(\frac{|w^Tx_i + b|}{\| w \|}\), 这也表示了一个点到超平面的距离

proof

我们 denote \(w^Tx + b = 0\)为超平面，那么对于任意一个点\(x_i\)，我们可以将其投影到超平面上，得到\(x_i'\)，那么有\(r = x_i - x_i' = r_0 w \Rightarrow x_i' = x_i - r_0 w\)

那么有

\[\begin{aligned} r_0 &= \frac{w^T x_i + b}{\| w \|} \end{aligned} \]

\(r_0\)的 abs 即为我们想要的距离

proof end

形式化想法

我们使用几何间隔来表示点到超平面的距离，那么 margin 即为

\[\text{margin}=\min_{i=1,2,\ldots,N} \frac{|w^Tx_i + b|}{\| w \|} \]

如果我们将标签\(y\)限制在集合\(\{ +1, -1 \}\)(为了方便优化),那么我们的目标函数即为

\[\max_{w,b} \min_{i=1,2,\ldots,N} \frac{|w^Tx_i + b|}{\| w \|} \\ \text{s.t. } y_i(w^Tx_i + b) \geq 0, \quad i = 1, 2, \ldots, N \]

去除绝对值，我们可以得到

\[\max_{w,b} \frac{1}{\| w \|} \min_{i=1,2,\ldots,N} y_i({w^Tx_i + b}) \\ \text{s.t. } y_i(w^Tx_i + b) \geq 0, \quad i = 1, 2, \ldots, N \]

形式上依旧可以简化，一个想法是对于一个分式，我们可以通过限制其中一项，来优化另一项，可以得到相同的解，即

\[\arg \max \frac{f(x)}{g(x)} \iff \arg \max \frac{c f(x)}{c g(x)} \iff \arg \max f(x), \quad s.t. \ g(x) = c \]

于是我们可以通过限制 margin 的值，来优化 \(w, b\)，即限制\(\min_{i=1,2,\ldots,N} y_i({w^Tx_i + b}) = 1\)

于是我们可以得到最终形式

\[\min_{w,b} \frac{1}{2} \| w \|^2 \\ \text{s.t. } y_i(w^Tx_i + b) \geq 1, \quad i = 1, 2, \ldots, N \]

这是一个凸二次规划问题，Dual Gap 为 0，因此我们可以通过求解对偶问题来求解原问题，即使用 KKT 条件来求解原问题。

然而值得注意的是，使用对偶问题的好处在于我们能够使用 Kernel function 将原问题映射到高维空间，从而解决线性不可分的问题，对于求解时间的提升并不明显，甚至于说，对于线性可分的问题，我们可以直接求解原问题，而不需要使用对偶问题（\(\mathcal{O}(n^{1.x})\)）。

Hard Margin-SVM

\[\max_{\alpha} \min_{w,b} \frac{1}{2} \| w \|^2 + \sum_{i=1}^N \alpha_i (1 - y_i(w^Tx_i + b)) \\ \text{s.t. } \alpha_i \geq 0, \quad i = 1, 2, \ldots, N \]

\[\begin{aligned} \mathcal{L}(w, b, \alpha) &= \frac{1}{2} \| w \|^2 + \sum_{i=1}^N \alpha_i (1 - y_i(w^Tx_i + b)) \end{aligned} \]

求一下偏导数（KKT 条件的一部分，也是最小值的必要条件）:

\[\begin{aligned} \frac{\partial \mathcal{L}(w, b, \alpha)}{\partial w} &= w - \sum_{i=1}^N \alpha_i y_i x_i = 0 \\ \Rightarrow w & = \sum_{i=1}^N \alpha_i y_i x_i \\ \frac{\partial \mathcal{L}(w, b, \alpha)}{\partial b} &= -\sum_{i=1}^N \alpha_i y_i = 0 \\ \end{aligned} \]

代入 \(w, b\)，我们可以得到对偶问题

\[\mathcal{L}(w, b, \alpha) = \frac{1}{2} \| w \|^2 + \sum_{i=1}^N \alpha_i (1 - y_i(w^Tx_i + b)) = \\ \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j + \sum_{i=1}^N \alpha_i - \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j = \\ \sum_{i=1}^N \alpha_i - \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j \]

因此，我们可以得到对偶问题

\[\max_{\alpha} \sum_{i=1}^N \alpha_i - \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j \\ \text{s.t. } \alpha_i \geq 0, \quad i = 1, 2, \ldots, N \\ \sum_{i=1}^N \alpha_i y_i = 0 \]

我们如果想要对偶问题有意义且和原问题有对应关系（对于 QP 是强对偶关系），那么我们需要满足 KKT 条件，即

\[\begin{aligned} \frac{\partial \mathcal{L}(w, b, \alpha)}{\partial w} &= w - \sum_{i=1}^N \alpha_i y_i x_i = 0 \\ \Rightarrow w & = \sum_{i=1}^N \alpha_i y_i x_i \\ \frac{\partial \mathcal{L}(w, b, \alpha)}{\partial b} &= -\sum_{i=1}^N \alpha_i y_i = 0 \\ 1 - y_i(w^Tx_i + b) &\leq 0 \\ \alpha_i &\geq 0 \\ \alpha_i (1 - y_i(w^Tx_i + b)) &= 0 \end{aligned} \]

此时\(v(D) = v(P)\), 同时\(\alpha^\star\)即对应原问题 KKT 点的乘子。

\(w^\star, b^\star\)可以通过 KKT 求解

\[w^\star = \sum_{i=1}^N \alpha_i^\star y_i x_i \\ \alpha_i^\star (1 - y_i(w^{\star T}x_i + b^\star)) = 0 \]

那么对于\(1 - y_i(w^{\star T}x_i + b^\star) = 0\)的点，我们拥有\(\alpha_i^\star \geq 0\)，我们称之为 支持向量，只要寻找到一个就可以求解\(b^\star\)

\[b^\star = y_i - \sum_{j=1}^N \alpha_j^\star y_j x_j^T x_i \]

然而在实际过程中，为了减少误差，我们可以求解所有支持向量的平均值。

在求解过程中的有趣的现象

1. 首先我们看对偶问题的目标函数

   \[\max_{\alpha} \sum_{i=1}^N \alpha_i - \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j \\ \text{s.t. } \alpha_i \geq 0, \quad i = 1, 2, \ldots, N \\ \sum_{i=1}^N \alpha_i y_i = 0 \]

   观察\(\sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j\)，可以将其写成一个二次型\((\alpha y)^T X^T X (\alpha y)\), 那么如果将\(X\)单位化，\(X^T X\)是一个相似性矩阵（考虑\(cos \theta\)）。不单位化也可以表示相似性,叫做Green Matrix。如果相似性表征不好，我们可以通过 Kernel function 来进行映射，比如 RBF Kernel：\(K(x_i, x_j) = \exp(-\gamma \| x_i - x_j \|^2)\)。

   那么 SVM 的学习过程可以看作是在一个相似性空间中进行的，类别相同的点在相似性空间中更加接近，而类别不同的点在相似性空间中更加远离。

2. 对偶问题中的约束

   \[\sum_{i=1}^N \alpha_i y_i = 0 \]

   每一个点都有一个乘子，对于不是支持向量的点，\(\alpha_i = 0\)，对于支持向量，\(\alpha_i > 0\)。

   正类与负类的乘子之和为 0，可以看作隐式的对正负类做了平衡性调节。

Soft Margin-SVM

Hard Margin-SVM 考虑的情况非常理想，而对于线性不可分的问题，我们无法求解，因此我们引入了 Soft Margin-SVM。

我们可以引入一个 loss function，对于每一个点，我们引入一个 \(\xi_i\)(也被称作 hinge loss，比感知机中的 loss 更加严格)，\(\xi_i = 0,\quad y_i(wx_i + b) \geq 0\), \(\xi_i = 1-y_i(wx_i + b), \quad y_i(wx_i + b) < 0\), 那么我们可以写出优化目标

\[\min_{w,b,\xi} \frac{1}{2} \| w \|^2 + C \sum_{i=1}^N \xi_i \\ \text{s.t. } y_i(wx_i + b) \geq 1 - \xi_i, \quad i = 1, 2, \ldots, N \\ \xi_i \geq 0, \quad i = 1, 2, \ldots, N \]

依旧考虑对偶问题求解，我们可以得到

\[\max_{\alpha, \beta} \min_{w, b} \frac{1}{2} \| w \|^2 + C \sum_{i=1}^N \xi_i + \sum_{i=1}^N \alpha_i (1 - \xi_i - y_i(wx_i + b)) - \sum_{i=1}^N \beta_i \xi_i \\ \text{s.t. } \alpha_i \geq 0, \quad i = 1, 2, \ldots, N \\ \beta_i \geq 0, \quad i = 1, 2, \ldots, N \]

因此，KKT 条件为

\[\begin{aligned} \frac{\partial \mathcal{L}(w, b, \xi, \alpha, \beta)}{\partial w} &= w - \sum_{i=1}^N \alpha_i y_i x_i = 0 \\ \Rightarrow w & = \sum_{i=1}^N \alpha_i y_i x_i \\ \frac{\partial \mathcal{L}(w, b, \xi, \alpha, \beta)}{\partial b} &= -\sum_{i=1}^N \alpha_i y_i = 0 \\ \frac{\partial \mathcal{L}(w, b, \xi, \alpha, \beta)}{\partial \xi_i} &= C - \alpha_i - \beta_i = 0 \\ 1 - \xi_i - y_i(w^Tx_i + b) &\leq 0 \\ \xi_i &\geq 0 \\ \alpha_i &\geq 0 \\ \beta_i &\geq 0 \\ \alpha_i (1 - \xi_i - y_i(w^Tx_i + b)) &= 0 \\ \beta_i \xi_i &= 0 \end{aligned} \]

那么根据上述条件，我们可以得到对偶问题

\[\max_{\alpha} \sum_{i=1}^N \alpha_i - \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j \\ \text{s.t. } 0 \leq \alpha_i \leq C, \quad i = 1, 2, \ldots, N \\ \sum_{i=1}^N \alpha_i y_i = 0 \]

在求解过程中有趣的现象

1. 对于 Soft Margin-SVM，我们引入了一个超参数 \(C\)，用于调节 margin 的大小（$| w | $做的事情），当 \(C\) 较大时，我们会更加关注 margin 的大小，而当 \(C\) 较小时，我们会更加关注分类的准确性。

2. 从正则化的角度来看，我们可以将 Hard Margin-SVM 看作是 \(C \rightarrow \infty\) 的 Soft Margin-SVM，从而只优化结构风险；而 Soft Margin-SVM 则是在结构风险和经验风险之间做了一个权衡。

3. 由于\(\alpha_i + \beta_i = C\), 那么如果\(\alpha_i = 0\), 样本在 margin 外；如果\(\alpha_i = C\), 样本在 margin 内；如果\(0 < \alpha_i < C\), 样本在 margin 上。

4. 在计算\(b\)的时候，我们依旧需要找到支持向量，但是我们需要找到在 margin 上的支持向量，即\(0 < \alpha_i < C\)。

Kernel SVM

对于线性不可分的问题，我们可以通过 Kernel function 将原问题映射到高维空间，从而解决线性不可分的问题。

例如，我们可以用内积将原问题映射到高维空间，

\[x = (x_1, x_2), \quad z = (z_1, z_2)\\ \phi(x) = (x_1^2, \sqrt{2}x_1x_2, x_2^2) \\ K(x,z) = \phi(x)^T \phi(z) = x_1^2z_1^2 + 2x_1x_2z_1z_2 + x_2^2z_2^2 = (x_1z_1 + x_2z_2)^2 \]

于是，我们可以使用一个 Kernel function 来将原问题映射到高维空间，从而解决线性不可分的问题。对于某些满足条件的 K，一定存在一个 Mapping\(\phi: \mathbb{R}^n \to \phi\), 使得\(K(x,z) = \phi(x)^T \phi(z)\)。

其中\(\phi\)是特征空间，可以是无穷维的内积空间，但是我们不需要知道\(\phi\)的具体形式，只需要知道\(K\)的形式即可。

对于 Kernel 的限制条件

Mercer Condition：对于一个 Kernel function，如果其对应的 Gram 矩阵是半正定的，那么这个 Kernel function 是有效的。

即我们需要判定 K = [\(k(x_i, x_j)\)] 的半正定性。

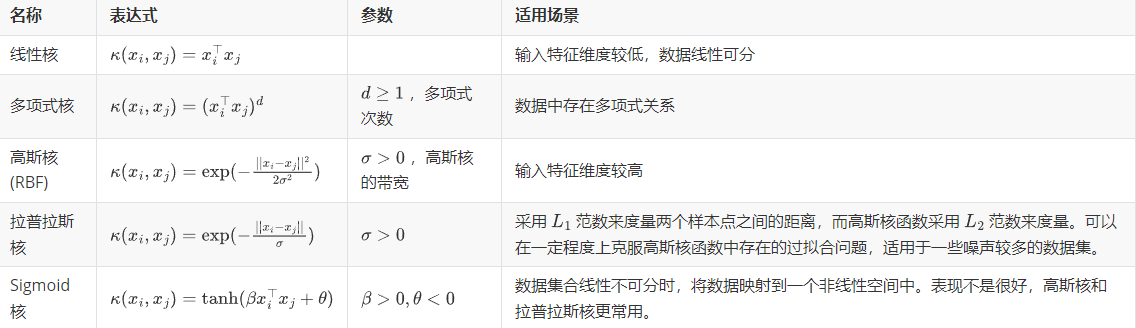
常见的 Kernel

时间复杂度

支持向量机（SVM）的时间复杂度取决于具体的训练算法和数据集的特性。以下是 SVM 训练和推理时间复杂度的一般情况：

训练时间复杂度

1. 线性 SVM:
   • 使用线性核的 SVM，如线性支持向量分类器（LinearSVC），其训练时间复杂度大约为 (O(n \times d))，其中 (n) 是样本数量，(d) 是特征数量。
2. 非线性 SVM:
   • 使用非线性核（如高斯核、RBF 核）的 SVM，训练时间复杂度大约为 (O(n^2 \times d)) 到 (O(n^3 \times d))。这个复杂度主要由计算核矩阵和解决二次规划问题所引起的。

推理时间复杂度

1. 线性 SVM:
   • 推理时间复杂度为 (O(d))，因为推理时只需计算一个线性函数。
2. 非线性 SVM:
   • 推理时间复杂度为 (O(n \times d))，因为每次推理都需要计算所有支持向量和测试样本之间的核函数值并加权求和。

这些复杂度表明，线性 SVM 在处理大规模高维数据时具有显著的计算优势，而非线性 SVM 在小规模或低维数据集上的表现可能更优，但计算成本更高。

根据实际使用场景，可能会选择不同的 SVM 算法以平衡精度和计算开销。例如，在处理大数据集时，可能更倾向于使用线性 SVM 或一些近似算法如线性近似核（Linear Approximations of Non-linear Kernels）。