KKT&Dual

KKT

问题引入

我们考虑一个最优化问题：

$$\begin{aligned} (P)&\min f(x) \\ &\text{s.t. } g_i(x) \leq 0, \quad i = 1, 2, \ldots, m \\ &h_i(x) = 0, \quad i = 1, 2, \ldots, p \end{aligned}$$

假设问题拥有三个不等式约束和一个等式约束，在$x^\star$处应该会满足如下图的条件：

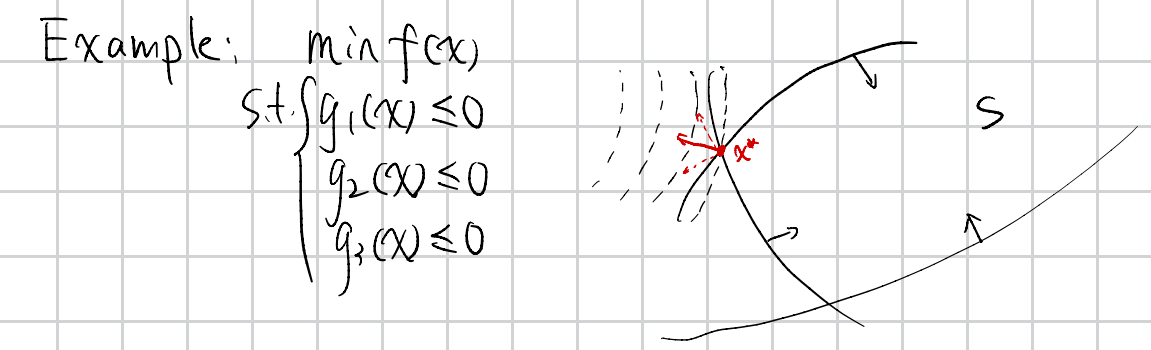
即在$x^\star$处，$f(x)$的负梯度方向（正交于约束曲面，因为不正交就可以沿着方向移动）可以表示为部分约束的梯度方向的线性组合，即

$$\nabla f(x^\star) = -\lambda_1 \nabla g_1(x^\star) - \lambda_2 \nabla g_2(x^\star)$$

其中$\lambda_1, \lambda_2 \geq 0$。

那么为了上述等式更加规范化，我们将$g_3(x)$也加入到约束中，即

$$\nabla f(x^\star) = -\lambda_1 \nabla g_1(x^\star) - \lambda_2 \nabla g_2(x^\star) - \lambda_3 \nabla g_3(x^\star) \\ \lambda_1, \lambda_2\geq 0, \ \lambda_3 = 0$$

可以将约束条件写为

$$\lambda_i g_i(x) = 0, \quad i = 1, 2, 3$$

直观地想，这是一个必要条件，因为很多地方都能满足这个条件，但是不一定是最优解。

那么如何将这样一个想法转化为一个标准的条件，这就是 KKT 条件的作用。

KKT 条件简述

KKT 条件：对于一个最优化问题，如果$x^\star$是一个局部最优解，且在$x^\star$处满足某一种 constraint qualification，那么最优解满足以下条件：

$$\begin{aligned} &\nabla f(x^\star) + \sum_{i=1}^m \lambda_i \nabla g_i(x^\star) + \sum_{i=1}^p \mu_i \nabla h_i(x^\star) = 0 \\ &\lambda_i \geq 0, \quad i = 1, 2, \ldots, m \\ &g_i(x^\star) \leq 0, \quad i = 1, 2, \ldots, m \\ &h_i(x^\star) = 0, \quad i = 1, 2, \ldots, p \\ &\lambda_i g_i(x^\star) = 0, \quad i = 1, 2, \ldots, m \end{aligned}$$

我们称满足条件的$\lambda_i, \mu_i$为拉格朗日乘子。

其中，第(1)(2)个条件称作Dual Feasibility，第(3)(4)个条件称作Primal Feasibility，第(5)个条件称作Complementary Slackness。

可以想象，$g_i(x^\star) < 0$对最优解的梯度方向不起作用。

其实可以指出，KKT 条件是一个必要条件，而不是充分条件。

KKT 条件的推导

证明 KKT 条件涉及三个集合、一个 constraint qualification 和 Farkas 引理，理论性较强，这里不做详细推导。

Dual Problem

我们依旧考虑上面提及的 Primal Problem

$$\begin{aligned} (P)&\min f(x) \\ &\text{s.t. } g_i(x) \leq 0, \quad i = 1, 2, \ldots, m \\ &h_i(x) = 0, \quad i = 1, 2, \ldots, p \end{aligned}$$

可行集合为

$$S = \{x \in \mathbb{R}^n | g_i(x) \leq 0, h_i(x) = 0\}$$

为什么我们需要从 Primal Problem 转化为 Dual Problem 呢？因为

1. 如果 P 问题非凸，求解原问题是一个 NP-hard 问题，而 Dual Problem 可能是一个凸优化问题
2. 当 P 问题是一个凸优化问题时，Dual Problem 可以帮助我们理解问题的几何性质
3. Dual Problem 可以帮助我们理解问题的最优解

拉格朗日对偶函数

我们定义拉格朗日函数

$$\mathcal{L}(x, \lambda, \mu) = f(x) + \sum_{i=1}^m \lambda_i g_i(x) + \sum_{i=1}^p \mu_i h_i(x),\quad x \in X, \lambda \geq 0$$

拉格朗日对偶函数定义为

$$dual(\lambda, \mu) = \inf_{x \in X} \mathcal{L}(x, \lambda, \mu)_{\quad \lambda_i \geq 0}$$

我们可以得到如下不等式：

$$dual(\lambda, \mu) = \inf_{x \in X} \mathcal{L}(x, \lambda, \mu)_{\quad \lambda_i \geq 0} \\ \leq \inf_{x \in S} \mathcal{L}(x, \lambda, \mu)_{\quad \lambda_i \geq 0} \\ \leq \inf_{x \in S} f(x)$$

如果我们 denote 原问题最优值为$p^\star$记为$v(p)$，那么我们可以得到如下结论：

$$\forall \lambda \geq 0, \mu, \quad dual(\lambda, \mu) \leq p^\star$$

即对偶函数是原问题最优值的下界。

拉格朗日对偶问题(求一个最大下界)

我们定义拉格朗日对偶问题为

$$\begin{aligned} (D)&\max dual(\lambda, \mu) \\ &\text{s.t. } \lambda_i \geq 0, \quad i = 1, 2, \ldots, m \end{aligned}$$

如果我们将对偶函数写开，则对偶问题可以写为

$$\begin{aligned} (D)&\max_{\lambda,\mu} \min_{x \in X} \mathcal{L}(x, \lambda, \mu) \\ &\text{s.t. } \lambda_i \geq 0, \quad i = 1, 2, \ldots, m \end{aligned}$$

如果我们考虑将最小值和最大值交换，那么可以得到如下问题

$$\begin{aligned} &\min_{x \in X} \max_{\lambda,\mu} \mathcal{L}(x, \lambda, \mu) \\ &\text{s.t. } \lambda_i \geq 0, \quad i = 1, 2, \ldots, m \end{aligned}$$

对于这个优化问题

1. 如果$\exist i, g_i(x) > 0$，那么最大值为无穷大
2. 如果$\exist i, h_i(x) \neq 0$，那么最大值为无穷大
3. 如果$\forall i, g_i(x) \leq 0, h_i(x) = 0$，那么最大值为$f(x)$，则此时可以等价为 Primal Problem

因此，这个问题，值希望有界的话，实际上与 Primal Problem 等价，即

$$\min_{x \in X} \max_{\lambda \geq 0, \mu} \mathcal{L}(x, \lambda, \mu) \iff \min \{\min_{x \in S} f(x), \infin \} \iff \min_{x \in S} f(x)$$

弱对偶定理

在前面我们已经得到了$d(\lambda, \mu) \leq v(P)$的结论，对于任意的$\lambda \geq 0, \mu$。

那么对于对偶问题，我们如果我们 denote 对偶问题最优值为$d^\star = v(D)$，那么我们可以得到如下结论：

$$\forall \lambda_i \geq 0, \quad d(\lambda, \mu) \leq v(D) \leq v(P) \leq f(x)$$

可以形象理解为鸡头和凤尾的关系。

Dual Gap

我们定义对偶问题和原问题的差距为 Dual Gap，即

$$\text{Dual Gap} = v(P) - v(D)$$

可以映射到几何空间中

强对偶定理

一个凸优化问题可以被涉及成不满足强对偶问题的情况，因此在凸优化问题外，还要满足一个条件。

假设（充分条件）：

1. (凸优化)X 是非空凸集，$f, g_i$ 是凸函数，$h_i$是仿射函数。（原问题是凸优化问题）
2. (Slater Condition)$\exist \hat{x} \in X, \quad \text{s.t.} \quad g_i(\hat{x}) < 0, h_i(\hat{x}) = 0$（有一个严格可行点），同时 0 是一个$h(x)$的内点。（这个条件最常用的是 Slater Condition）
   • Slater Condition：$\exist \hat{x} \in relint \mathcal{D}, \quad \text{s.t.} \quad g_i(\hat{x}) < 0, h_i(\hat{x}) = 0$

那么我们可以得到如下结论：

$$v(P) = v(D) \iff \min f(x) = \max d(\lambda, \mu)$$

证明略...

于是，对于强对偶问题，我们只需要分别对函数中的$\lambda, \mu$和原问题中的$x$进行偏导=0 即可。

对偶问题的性质

对偶函数是一个凹函数

$$dual(\lambda, \mu) = \min_{x \in X} \mathcal{L}(x, \lambda, \mu)_{\quad \lambda_i \geq 0}$$

其中若将$x$看作一个参数，那么$\mathcal{L}(x, \lambda, \mu)$是一个关于$\lambda, \mu$的仿射函数，因此对偶函数是一个凹函数。

所以$\max \text{concave} \iff \min \text{convex}$，对偶问题一定是一个凸优化问题。

KKT 条件与对偶问题

一个凸优化问题，只要是强对偶的，一定满足 KKT 条件（必要条件）。因此，我们可以通过求解对偶问题来求解原问题。

对偶问题的求解方法就是先构建拉格朗日函数，然后先对$x$求梯度，然后对$\lambda, \mu$求最大值。

对于凸优化

1. 如果$x^\star$满足 KKT 条件，那么$x^\star$是原问题的最优解，且对偶问题的最优解是 KKT 条件中的乘子。

2. 如果 Slater Condition 满足，那么原问题的最优解的 KKT 点乘子与对偶问题的最优解相等。