EM Algorithm
1. GMM 引入
若数据服从一个高斯分布,可以用 MLE + 偏导为 0 的方法求解参数,其中框架如下
\[\theta = \{ \mu, \Sigma \} = \arg \max_{\theta} \sum_{i=1}^N \log p(x_i | \theta)
\]
而由于单个高斯分布概率密度函数为 concave,因此整体的似然函数也是 concave 的,梯度为 0 点即为最优解。
然而,若数据服从多个高斯分布,density function 为
\[p(x) = \sum_{k=1}^K \pi_k \mathcal{N}(x | \mu_k, \Sigma_k) \\
\quad s.t. \sum_{k=1}^K \pi_k = 1
\]
若使用 MLE 方法,log likelihood 为
\[LL = \sum_{i=1}^N \log p(x_i) = \sum_{i=1}^N \log \sum_{k=1}^K \pi_k \mathcal{N}(x_i | \mu_k, \Sigma_k)
\]
由于 density function 不再是凹函数,同时\(\log\)中还有求和项计算复杂,因此无法直接求解最优解,此时可以引入 EM 算法,为一个迭代算法。
ex: 隐变量理解/生成过程
我们可以将 GMM 理解为一个带有隐变量的模型,即每一个样本都有一个对应的隐变量,表示该样本属于哪一个高斯分布,我们可以将其表示为\((x_i, z_i)\),其中 \(z_i\) 表示样本 \(x_i\) 的隐变量。
\[p(x_i) = \sum_{k=1}^K p(z_i=k) p(x_i | z_i=k) = \sum_{k=1}^K \pi_k \mathcal{N}(x_i | \mu_k, \Sigma_k)
\]
而对于生成过程,我们可以认为是选定了一个隐变量取值后,再生成样本,即
\[x \approx p(x|z) = \mathcal{N}(x | \mu_z, \Sigma_z)
\]
2. EM 算法框架
EM 算法的迭代过程如下
\[\begin{align}
\theta^{(t+1)} = \arg \max_{\theta} \text{E}_{p(z|x;\theta^{(t)})}[\text{log} p(x,z;\theta)] = \arg \max_{\theta} \int_z p(Z | X, \theta^{(t)}) \log p(X, Z | \theta)
\end{align}
\]
3. EM 算法直观理解
对于 n 个数据\((x_1, \dots,x_N)\),MLE 如下:
\[\theta = \arg \max_{\theta}\sum_N \log p(x_i|\theta)
\]
若带有隐变量\(z=(z_1,\dots,z_k)\),则有
\[\theta = \arg \max_{\theta}\sum_N \log p(x_i|\theta) = \arg \max_{\theta}\sum_N \log \sum_z p(x_i,z_j|\theta)
\]
由于直接求解困难,因此使用\(z\)的分布放缩:
\[\sum_N \log \sum_z p(x_i,z|\theta) = \sum_N \log \sum_z q(z_j) \frac{p(x_i,z_j|\theta)}{q(z_j)} \geq \sum_N \sum_z q(z_j) \log \frac{p(x_i,z_j|\theta)}{q(z_j)}
\]
我们对似然函数的下界进行最大化
\[\theta = \arg \max_{\theta} \sum_N \sum_z q(z_j) \log \frac{p(x_i,z_j|\theta)}{q(z_j)} \\
\iff \arg \max \sum_N \sum_z q(z_j) \log p(x_i,z_j|\theta) \\
\iff \arg \max \sum_z \sum_N q(z_j) \log p(x_i,z_j|\theta) \\
\iff \arg \max \sum_z q(z_j) \sum_N \log p(x_i,z_j|\theta) \\
\iff \arg \max \mathbb{E}_{q(z)} [\log p(X,z|\theta)]
\]
上述过程描述了\(LL(\theta)\)的下界,EM 算法的直观理解就是在每次迭代开始时,我们先对\(LL(\theta)\)求下界,然后求下界的最大值,然后再对下界求最大值,如此循环。
这样理解比较抽象,因为我们还没有导出下界与 LL 之间的差距,我们在下一节详细分析具体过程。
4. EM 算法:变分推断理解
变分推断实际上是一种近似推断方法,我们希望使用一种我们更加熟悉的分布来推断出未知的分布,可以将已知分布作为未知分布的下界迭代求解。
我们需要对似然函数进行分解,求得下界与 LL 之间的关系。
\[\log P(X;\theta) = \log P(X,Z;\theta) - \log P(Z|X;\theta) \\
\iff \log P(X;\theta) = \log \frac{P(X,Z;\theta)}{q(Z)} - \log \frac{P(Z|X;\theta)}{q(Z)} \\
\]
两边分别对 \(q(Z)\) 求期望,有
\[\log P(X;\theta) = \underbrace{\int_Z q(Z) \log \frac{P(X,Z;\theta)}{q(Z)} dZ}_{\text{ELBO}} + \underbrace{- \int_Z q(Z) \log \frac{P(Z|X;\theta)}{q(Z)} dZ}_{\text{KL(q || p)}}
\]
其中 ELBO 为下界,KL 为 KL 散度(\(KL \geq 0\)),我们需要最大化 ELBO,即使得下界尽可能接近 LL,因此我们可以得知,下界与似然函数之间的差距是一个 KL 散度,这非常好,因为 KL 散度是非负的。
对于似然函数\(LL\),有两方面可以影响其大小,一个是\(\theta\),一个是\(q\)。
-
对于当\(\theta = \theta_t\),\(q(Z) = P(Z|X;\theta^t)\),在 E-step 则\(log P(X;\theta^t) = \text{ELBO}({\theta^t})\)
-
在 M-step 中,我们沿用 E-step 的\(q(Z)\), 而没有限制\(\theta\),需要最大化 ELBO,即
\[\arg \max \text{ELBO}(\theta) = \arg \max \int_Z q(Z) \log \frac{P(X,Z;\theta)}{q(Z)} dZ
\]
此时的 ELBO 比 E-step 的 ELBO 要大,同时 KL 散度也会上升,因此,似然函数比上一轮的似然函数要大。
5. EM 算法:图像辅助理解(图像来自于 PRML)
上一节说到每一轮的 ELBO 都比上一轮的 ELBO 要大,KL 散度也会上升,因此似然函数也会上升,我们可以通过图像来辅助理解。
-
没有指定 \(\theta\) 与 \(q\) 时
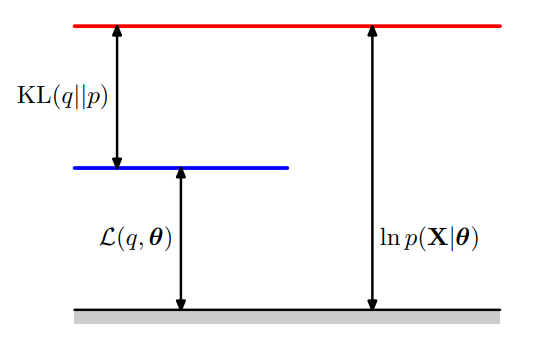
-
指定了 \(\theta^{\text{old}}\) 与 \(q(Z) = p(Z|X;\theta^{\text{old}})\)时
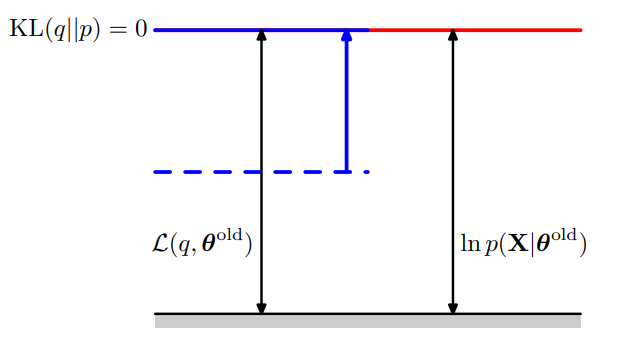
-
沿用 E-step 的 \(q(Z)\), 在 M-step 中最大化 ELBO
此时 ELBO 提升,KL 提升,导致 LL 提升
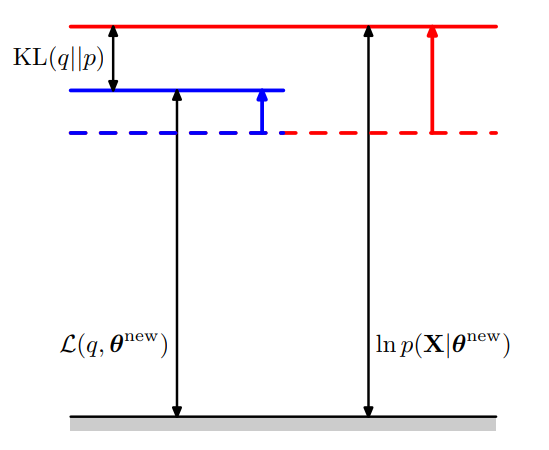
-
使用函数图像来一图流解决
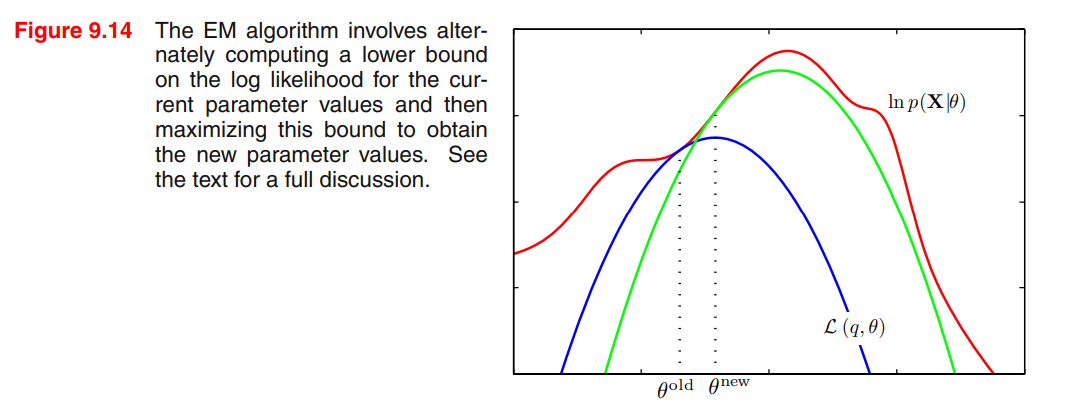
6. EM 算法收敛性证明
我们将上述理解转化为数学证明,证明 EM 算法的收敛性。
迭代算法欲证明收敛性,只需要证明每次迭代后的 log likelihood 均不减少即可,即:
\[LL(\theta^{(t+1)}) \geq LL(\theta^{(t)}) \\
p(X|\theta^{(t+1)}) \geq p(X|\theta^{(t)}) \\
\text{log} p(X|\theta^{(t+1)}) \geq \text{log} p(X|\theta^{(t)})
\]
\(proof\):
\[\text{log} p(X|\theta) = \text{log} p(X,Z|\theta) - \text{log} p(Z|X,\theta) \\
\]
对两边求期望,有
\[\text{E}_{p(Z|X,\theta^{(t)})}[\text{log} p(X|\theta)] = \text{E}_{p(Z|X,\theta^{(t)})}[\log p(X,Z|\theta)] - \text{E}\_{p(Z|X,\theta^{(t)})}[\text{log} p(Z|X,\theta)]
\]
由于左边与\(Z\)无关,因此有
\[\text{log} p(X|\theta) = \text{E}_{p(Z|X,\theta^{(t)})}[\text{log} p(X,Z|\theta)] - \text{E}_{p(Z|X,\theta^{(t)})}[\text{log} p(Z|X,\theta)]
\]
右边展开为积分形式,有
\[\text{log} p(X|\theta) = \underbrace{\int p(Z|X,\theta^{(t)}) \text{log} p(X,Z|\theta) dz}_{Q(\theta,\theta^{(t)})} - \underbrace{\int p(Z|X,\theta^{(t)}) \text{log} p(Z|X,\theta) dz}_{H(\theta,\theta^{(t)})}
\]
由于 EM 算法的形式,可知最大化 \(Q\)项,因此有
\[Q(\theta^{t+1},\theta^{(t)}) \geq Q(\theta,\theta^{(t)})
\]
即有
\[Q(\theta^{(t+1)},\theta^{(t)}) \geq Q(\theta^{(t)},\theta^{(t)})
\]
那么若要证明 EM 算法的收敛性,只需要证明 \(H\) 项的减少即可。
\[H(\theta^{(t+1)},\theta^{(t)}) \leq H(\theta^{(t)},\theta^{(t)})
\]
即证
\[H(\theta,\theta^{(t)}) \leq H(\theta^{(t)},\theta^{(t)}) \\
H(\theta^{(t)},\theta^{(t)}) - H(\theta,\theta^{(t)}) \geq 0
\]
展开即有
\[\int p(Z|X,\theta^{(t)}) \text{log} \frac{p(Z|X,\theta^{(t)})}{p(Z|X,\theta)} dz = KL(p(Z|X,\theta^{(t)})\| p(Z|X,\theta)) \geq 0
\]
收敛性得证,但无法证明收敛到全局最优解。
\(proof\) end
7. EM 求解 GMM
我们现在尝试使用 EM 算法求解 GMM 的参数。
我们求解的目标是\(\theta = \{ \pi, \mu, \Sigma \}\)
我们假设样本集合为\(\{x_1, x_2, \cdots, x_N\}\),每一对\((x_i,z_i)\)相互独立,即\(p(X,Z) = \prod_{i=1}^N p(x_i, z_i)\)
在 GMM 中,我们定义\(p(x,z;\theta)\)
\[p(X,Z;\theta) = \prod_{i=1}^N p(x_i,z_i;\theta_k) = \prod_{i=1}^N p(z_i) p(x_i|z_i) = \prod_{i=1}^N \pi_{z_i} \mathcal{N}(x_i|\mu_{z_i}, \Sigma)
\]
定义\(p(z|x;\theta)\)
\[p(Z=(\dots)|x; \theta) = p(z_1, \dots, z_N | x_1, \dots, x_N) =\prod_{i=1}^N p(z_i|x_i;\theta)
\]
\[p(z_i=k|x_i;\theta) = \frac{p(x_i|z_i=k)p(z_i=k)}{\sum_{k=1}^K p(x_i|z_i=k)p(z_i=k)}
\]
E-step:
\[\mathbb{E}_{p(Z|X;\theta^t)}[\log p(X,Z;\theta)] =
\sum_{k} p(Z|X;\theta^t) \log p(X,Z;\theta) = \\
\sum_{z_1 = 1}^K \cdots \sum_{z_N = 1}^K \prod_{i=1}^N p(z_i|x_i;\theta^t) (\log \prod_{i=1}^N \pi_{z_i} \mathcal{N}(x_i|\mu_{z_i}, \Sigma)) = \\
\sum_{z_1 = 1}^K \cdots \sum_{z_N = 1}^K (\prod_{i=1}^N p(z_i|x_i;\theta^t) )\sum_{i=1}^N (\log \pi_{z_i} + \log \mathcal{N}(x_i|\mu_{z_i}, \Sigma)) = \\
\sum_{i=1}^N \sum_{z_1 = 1}^K \cdots \sum_{z_N = 1}^K \prod_{i=1}^N p(z_i|x_i;\theta^t)(\log \pi_{z_i} + \log \mathcal{N}(x_i|\mu_{z_i}, \Sigma)) = \\
\sum_{i=1}^N \sum_{k = 1}^K p(z_i=k|x_i;\theta^t)(\log \pi_{k} + \log \mathcal{N}(x_i|\mu_{k}, \Sigma))
\]
M-step:
\[(\pi^{t+1}, \mu^{t+1}, \Sigma^{t+1}) = \\ \arg \max_{\pi, \mu, \Sigma} \sum_{i=1}^N \sum_{k = 1}^K p(z=k|x_i;\theta^t)(\log \pi_{k} + \log \mathcal{N}(x_i|\mu_{k}, \Sigma)) \iff \\
\arg \max_{\pi, \mu, \Sigma} \sum_{i=1}^N \sum_{k = 1}^K p(z_i=k|x_i;\theta^t)\log \pi_{k} + \sum_{i=1}^N \sum_{k = 1}^K p(z=k|x_i;\theta^t) \log \mathcal{N}(x_i|\mu_{k}, \Sigma)
\]
后续优化细节参考 AML HW2
8. EM 算法进一步理解
\[\log P(X) = \mathcal{L}(q) + KL(q || Z|X)
\]
我们的目标是寻找到\(q \approx Z|X\)
当\(p(Z|X)\)非常复杂时,我们可以使用一个简单的\(q\)来近似\(p(Z|X)\),即可以借助变分推断,假设
\[q(Z) = \prod_{i=1}^N q(z_i)
\]
那么
\[\mathcal{L}(q) = \int q(Z) \log \frac{P(X,Z)}{q(Z)} dZ = \int \prod_{i=1}^N q(z_i) \log \frac{P(X,Z)}{q(Z)} dZ \\
= \int \prod_{i=1}^N q(z_i) \log \frac{P(X,Z)}{\prod_{i=1}^N q(z_i)} dZ = \int \prod_{i=1}^N q(z_i) \log P(X,Z) dZ - \int \prod_{i=1}^N q(z_i) \log \prod_{i=1}^N q(z_i) dZ \\
\]
...
参考
Pattern Recognition and Machine Learning, Bishop
EM 算法详解
徐亦达机器学习:Expectation Maximization EM 算法 【2015 年版-全集】






