二进制运算与加法器
对于计算机而言,由于存储机制的限制,所有的运算都是以二进制的形式进行的。这意味着计算机中的计算都是二元计算,要么0要么1,而至今为止计算机仍然无法很好地实现更高进制的直接运算,而二进制运算的情况足够少,这使得我们可以以布尔运算的形式实现两个二进制数字之间的运算。
布尔运算的基本运算类型有:与运算(&),或运算(|),非运算(~),异或运算(^)。其运算规则如下:
- 与:true & true = true,true & false = false,false & true = false,false & false = false
- 或:true | true = true,true | false = false,flase | true = true,false | false = false
- 非:~ true = false,~ false = true
- 异或:true ^ true = false,true ^ false = true,false ^ true = true,false ^ false = false
在计算机中,这些运算通过逻辑门(与门、或门、异或门、非门)实现,这里不对硬件层面的知识进行过多介绍。
对于二进制运算,我们有如下的运算规则:
0 + 0 = 0,0 + 1 = 1,1 + 0 = 1,1 + 1 = 0(进位)
将 0 作为flase,1 作为true,从而我们使用布尔运算中的异或运算模拟出二进制运算:
- 0+0 => false ^ false = false => 0
- 0+1 => false ^ true = true => 1
- 1+0 => true ^ false = true => 1
- 1+1 => true ^ true = false => (1) 0 (进位)
可以看到,我们使用布尔运算模拟了二进制下的运算规则,但问题在于,0+0 和 1+1 的结果都是0,但是后者需要一次进位。那么如何标记这个进位?
我们可以使用异或运算和一个与运算来实现对进位的标记,只有在参与运算的两个数字参与与运算的结果为true时才需要进位,即两个1(true)进行加法运算:
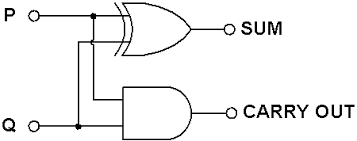
如上图所示,同时使用了异或运算与与运算后,这个运算会产生两个输出,一个加法运算结果和一个进位标记输出,我们成这个结构为一个“一位半加器”。之所以叫半加器是因为这个运算器只能对末尾的数字起作用,它没有考虑到之前的数位运算产生的进位。
高位数字的运算需要考虑三个输入:加数对应位上的数字、被加数对应位上的数字、以及前一位运算的进位。因此我们再向其中添加一个半加器,从而使用两次加法运算实现了高位数字的运算:
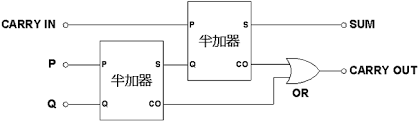
如上图所示,第一个加法器中首先计算了加数与被加数指定为上的数字,同时输出一个进位和一个和,然后在第二个半加器中计算这个和与上一位运算的进位输出的和,从而得到一个新的进位和这一位运算的最终结果。两个半加器生成了两个进位输出(这两个进位输出只可能产生0个或者1个进位,不会同时产生2个进位)。我们对这两个进位执行或运算,从而得到最终的进位结果,这个结果会输出给下一位运算的加法器。这样,我们就实现了一个“一位全加器”。
将8个这样的一位全加器组合起来,我们就构成了一个一个“八位全加器”,推广开来,我们也可以实现“十六位全加器”、“三十二位全加器”、“六十四位全加器”……
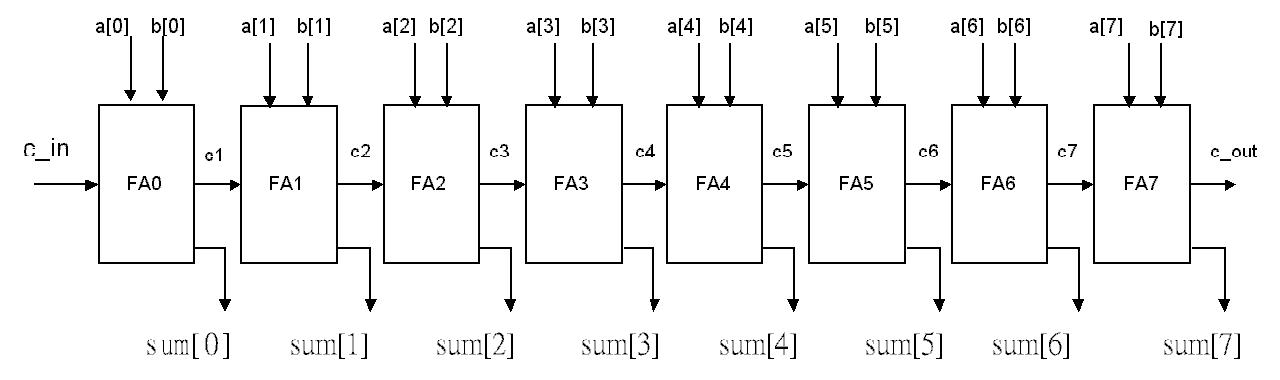
从图中可以看出,八位数字的运算过程是串行的,从低位开始的,逐级向高位进行推进,这意味这每一位的运算都要等待前一位运算完成才能进行,这也就意味着,如果我们要执行一次八位运算,其运算的时间将会是是一位运算的八倍。因此这种运算器也被称之为“逐位进位加法器”。因此,想要缩短多位数字的运算时间,将运算过程并行化是势在必行的。这也就是“选择进位加法器”的实现思想:在每一位的计算时,都在等待前一位的进位。那么不妨预先考虑进位输入的所有可能,对于二进制加法来说,就是0与1两种可能,并提前计算出若干位针对这两种可能性的结果。等到前一位的进位来到时,可以通过一个双路开关选出输出结果。不过,在这里不对选择进位加法器进行过多介绍。
但正如上面的示例,对于一个八位全加器而言,最高位的进位输出并没有被其他全加器接收,这个进位就被抛弃了,如果当进位不是0的时候,这个加法器的运算结果就不是本次运算的正确结果了,我们称这种情况为“运算溢出”。如 1100 0010 + 1000 1010 = 1 0100 1100,对于一个八位全加器而言,它的输出只能是0100 1100。
半加器和全加器统称为加法器,在CPU(中央处理器)中正是通过加法器执行数字计算。
二进制加法
二进制加法是最基础也是最简单的二进制运算。给定两个二进制数,如5和3,它们的和为8,转化为二进制运算如下:
5 的二进制表示为 0101
3 的二进制表示为 0011
5+3的二进制运算过程如下:
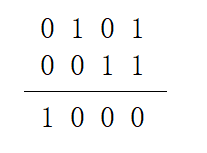
5+3的二进制结果为 1000,转换为十进制即 1 * 2^3 + 0 * 2^2 + 0 * 2^1 + 0 * 2^0 = 8。
但是对于6和12而言,它们的四位二进制表示分别为 0110 和 1100,而它们的和为 1 0010 = 18,在四位的处理器中,这个运算的输出就会是 0010 = 2,这也就是我们上面提到过的“运算溢出”。在某些系统中,发生溢出时会终止程序,报错提示;而在有的系统中则不会报错,而是如上面的示例一样,输出了移除后的数据,这将会导致运算结果的错误,最终影响到业务的准确性。因此,在进行运算时一定要考虑到是否会发生溢出,如果可能发生溢出则必须设计相应的机制,避免程序出错或者产生错误的结果。
无符号数和有符号数
我们知道,以0为分界线,数字分为正数和负数。在十进制中我们通过在数字前面加上 + / - 表示数字的正负(大概就是 0+X、0-X 的缩写),但是在计算机中是无法存储一个“正负号”的。所以我们只能另辟蹊径,约定二进制数字的第一个数字位(最左侧的位)为符号位,当符号位上数字为0的时候,当前数字为正数;符号位上数字位1的时候,当前数字为负数。这种将第一位作为符号位的数字,称之为“有符号数”,反之则称之为“无符号数”。
根据上面的规则,针对一个八位的二进制有符号数字,只有后七位是用于表示数值的。根据这种规则,一个八位二进制数字的范围应该为:[ 1111 1111 , 0111 1111],转换成十进制为:[-127,+127]。但我们知道,一个八位二进制的数字应该可以表示 2^8 = 256 个不同的数字,但是这里只有255个,还有一个去哪儿了?
考虑有符号数中的两个特殊数字(以八位二进制数为例):1000 0000和0000 0000。按照约定,这两个数字分别表示 -0 和 +0,但是对于0而言是不分正负的(0既不是整数也不是负数),那么这两个数字就重复了,我们可以拿其中一个数字来表示另外一个值,这样八位有符号数就可以表示 255+1=256 个数字了。这里我们有两种选择,将 1000 0000 作为 -128,或者是将 0000 0000 作为 +128。如何选择呢?
先说结论,我们选择了 1000 0000 作为 -128,而 0000 0000 表示 0。为什么要这么选择?
在解释这个问题之前,我们先了解一下 原码、反码和补码的概念。
原码、反码和补码
一个有符号二进制数,如 0110(6的二进制),这就是一个数字最初的样子,我们称之为“原码”。上面的二进制加法中,我们就是直接针对原码进行计算的。
如果我们要针对二进制设计减法,那么要如何设计?
二进制减法的运算规则为:
0 - 0 = 0,1 - 1 = 0,1 - 0 = 1,0 - 1 = 1(退位)
按照上面设计加法器的规则,我们可以很轻松的利用异或运算与或运算设计一套“减法器”。但是我们真的有必要在一个运算器中同时加入两套运算系统吗?
我们都知道,X - Y(其中X、Y都是正数)= X + (-Y),也就是说,减法可以被转换成加法。这意味着,通过一定的转换操作,我们可以使用一套加法器同时完成加法操作和减法操作。这样即可以减少运算器的设计和制造成本,一套运算系统出问题的概率相比两套也会更低。
那么要如何将一个二进制正数转换为对应的负数?
十进制数字在正负转换时只要在正数前面加上 - 即可,对于二进制而言,我们也可以通过将符号位转换为 1 来转换正负,如 +5 的二进制表示为 0101,-5 的二进制表示为 1101。但是这种简单粗暴的转换在运算时可以正确的运算吗?下面是 3+(-5) 的运算过程:

可以看到,简单粗暴的转换符号位在有符号数字计算时的计算结果并不正确,即使是在不去除溢出的情况下也不正确。理想的计算结果应该是 1010(-2)。这意味着我们需要考虑其他的转换方式。
虽然直接替换符号位并不可取,但有一件事情是必然的,-5+5=0,这意味这+5和-5的二进制表示的和也应该是0。我们尝试使用 0-5 的方式来计算 -5:
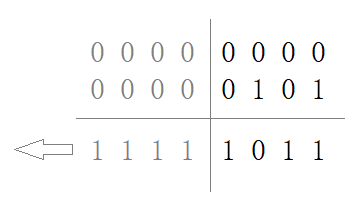
可以看到,我们直接使用 0000 去减 0101(5),最终可以得到一个二进制数字 1011,如果不舍弃溢出位,就可以看到,它的右侧有无数个1,这是因为不断向上借位的原因。如果我们直接舍弃掉这些溢出,用 0101 去加 1011,最终得到的结果就是 1 0000,这和我们期望的和为0并不符合(虽然在移除溢出位后的确表示为0,但这显然是不可取的)。
出现这种问题的原因就是上图的减法中的无限借位和运算溢出,那么我们干脆用 1000 替换掉 0 0000,这样就可以向最高位进行借位。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号