SCNU ACM 2016新生赛决赛 解题报告

新生初赛题目、解题思路、参考代码一览

A. 拒绝虐狗

Problem Description

CZJ 去排队打饭的时候看到前面有几对情侣秀恩爱,作为单身狗的 CZJ 表示很难受。
现在给出一个字符串代表 CZJ 前面的队列。你可以帮他一把把那些情侣分开吗?

Input

第一行是一个\(T\),代表数据的组数\(T\)（\(T\leq 100\)）。
每组一个只包含大写字母的字符串\(p\)（\(1\leq len_{p}\leq 1000\))，表示 CZJ 前面的队列，保证不会有连续三个及以上相同的字母序列

Output

将队列中相同且相相邻的字母用“1”隔开并输出。

Sample Input

2
AABB
ABBA

Sample Output

A1AB1B
AB1BA

解题思路

• 签到题，由于保证不会出现3个及以上的连续相同字符，所以每次判断一下上一个字符就好；
• 直接在线处理，时间复杂度\(O(len_{p})\)。

参考代码

#include <stdio.h>

int main() {
    int T;
    // 读入数据组数，并忽略本行回车
    scanf("%d%*c", &T);
    while (T--) {
        // 每次先初始化上一次读入的字符为EOF
        int readChar, lastChar = EOF;
        // 不断读入一个字符，直到回车
        while (readChar = getchar(), readChar != '\n') {
            // 如果读入的字符和上次读入字符相同，则先输出'1'分开
            if (readChar == lastChar) putchar('1');
            // 经过前面的处理后，把本次读入的字符输出
            putchar(readChar);
            // 重置上次读入的字符
            lastChar = readChar;
        }
        // 单个数据结束，输出换行
        putchar('\n');
    }
    return 0;
}

比赛提交代码中发现的问题

1. 有选手直接提交了exe、txt文件而不是源码文件，导致编译错误；
2. 部分选手对于循环理解有偏差，for(i=0; i<=n; i++)是执行n+1遍的，而数据只有n组，导致一直卡输入直至超时；
3. 部分选手误认为要读入全部数据后才能输出；实际上可以计算完一个情形后再读入下一个情形计算；
4. 接上一点，其中又有部分选手因此开了像char a[105][1600];的数组。在内存限制范围内开数组没问题，但是不能在main()等函数中开这么大的数组；详见C/C++堆栈空间分配；
5. 接上一点，其中又有部分选手开了大小刚好为1000的数组；实际上是对字符串的存储理解有偏差，字符串需要额外存储一个结束符'\0'，因此导致越界访问内存；
6. 有选手使用了C++的string类，但可惜基本功不扎实，存在错误使用；
7. 有选手一开始提交的代码中出现了“Please input ...”这样的输出，导致WA；
8. 有选手把==写成了=（比如if(a==1)成了if(a=1)），导致循环不结束直至TLE。

### B. Zyj 消极比赛

Problem Description

ACM 比赛剩下最后 10 分钟，其他人都已经收拾好东西准备走人，Zyj 才从睡梦中醒来。
Zyj 可以看到所有其他人的过题情况，他希望得到的名次在 a 到 b 之间，问有几种可选择的方案?
(假设其他人的提交时间即使加上罚时也早于 Zyj 的提交,毕竟剩下 10 分钟了都)

Input

第一行为 T （0 < T < 100），代表有 T 组数据。
每组数据中第一行为两个数字 m n a b，由空格隔开，代表这次比赛有 m 道题 (由于字母数量的限制，0 < m < 27)、
n 个其他人、Zyj 希望得到的名次 x 满足 a < x < b （ −1 < n, a, b < 1000）。
下一行为 Zyj 解决每道题需要的秒数 \(0\leq t_i < 999\)。
下面 n 行为每个人每道题的通过情况，1 为已通过，0 为未通过。

Output

对每个样例，输出 Case #k: ans，其中 k 为样例编号，ans 为方案数量。

Sample Input

1
4 1 0 2
300 300 300 300
0 0 0 1

Sample Output

Case #1: 6

Hint

样例解释:
Zyj 必须做出至少 2 题,又因为每个题的解题时间为 300 秒即 5 分钟,Zyj 也只能做最多 2 题,
所以 Zyj 做两题有 \(C_4^2 = 6\) 种方案。

解题思路

• 初赛这题是求组合数。但是你有没有想过为什么能用求组合数的方法来做呢？
• 还记得吗？初赛这道题没有对Zyj做每题作出限制。也正因为如此，Zyj无论做哪一题都是等价的，所以对于无序集合，我们可以求组合数。
• 但是这里更接近实际情况，Zyj做每一题的时间都是不一样的。有可能这道题做了，剩下的题就没时间做了。由于剩下的时间有限，这是个求满足特定条件的子集的问题。
• 能不能用枚举的方法呢？
  • 选一道题，根据剩下的时间再选一道题，重复下去，总能把所有情况列举出来。
  • 但是你想啊，一个大小为\(m\)的集合，它的非空子集有 $2^m-1 $个；
  • 一个不小心你可能需要 \(O(2^m)\) 到甚至 \(O(m!)\) （姿势不对时）的复杂度把所有可行子集都枚举出来。
• 枚举太暴力了，我们可以记忆化搜索。
  • 我们定义一个数组 dp[i][j][t] （\(j\leq i\)）来表示在总共有 \(i\) 道题，Zyj睡醒后剩下 \(t\) 时间的情况下，Zyj做 \(j\) 题的方案数。
  • 显然，对于任意 \(1\leq i\leq 26\)， \(0\leq t\leq 600\) （10分钟=600秒）， dp[i][0][t]=1 恒成立，均可算作1种情况。
  • 设 c[i] 代表Zyj做第 \(i\) 题所需的时间，显然， dp[i][i][t] = dp[i-1][i-1][t-c[i]]；
  • 而Zyj做 \(0<j<i\) 题时（dp[i][j][t]），不做第 \(i\) 题的方案数为 dp[i-1][j][t]，做第 \(i\) 题并在前面的题选做 \(j-1\) 题的方案数为 dp[i-1][j-1][t-c[i]]。
  • 综上，我们可以得出 dp[i][j][t] = { dp[i-1][j][t] + dp[i-1][j-1][t-c[i]], if \(j\leq i\) }, { 0, if j > i }, { 1, if j = 0 }。
• 时间复杂度 \(O(300m^2)\)；空间复杂度 \(O(600m^2)\)，用滚动数组优化到 \(O(600m)=15600\)。

参考代码

#include <stdio.h>
#include <string.h>

const int MaxTime = 600;
int m, n, a, b;
int dp[27][601];// dp[j][t]代表Zyj在t时间内做j题
int solveCount[27];// solveCount[i] 记录其他人做i题的人数

void init() {
    memset(dp, 0x0, sizeof(dp));
    for (int iterTime = 0; iterTime <= MaxTime; ++iterTime)
        dp[0][iterTime] = 1;
    memset(solveCount, 0x0, sizeof(solveCount));
}

void prepare() {
    int costTime;// 读入Zyj做每一题所需的时间
    for (int iterProb = 1; iterProb <= m; ++iterProb) {
        scanf("%d", &costTime);
        // j=0 的情况不需要处理，已经初始化好了
        // 由于使用了滚动数组，从大到小更新
        for (int iterSolv = iterProb; iterSolv > 0; --iterSolv)
            // 直接从Zyj解该题所需时间考虑，剩下时间小于该时间的话Zyj也解不出来
            for (int iterTime = costTime; iterTime <= MaxTime; ++iterTime)
                dp[iterSolv][iterTime] += dp[iterSolv - 1][iterTime - costTime];
    }
}

void readSolves() {
    // 读入n个人的做题情况
    for (int iterPerson = 0; iterPerson < n; ++iterPerson) {
        int acc = 0, solvedTag;// acc用于累加每个人做题总数，solvedTag表示是否解题
        for (int iterProb = 0; iterProb < m; ++iterProb) {
            scanf("%d", &solvedTag);
            acc += solvedTag;
        }
        // 累加总共做出acc道题的人数
        ++solveCount[acc];
    }
}

void read() {
    scanf("%d%d%d%d", &m, &n, &a, &b);
    prepare();
    readSolves();
}

int work() {
    // rank代表Zyj做i题以上能拿的名次
    // Zyj有拿第一的可能，但也一定是同题数的最后一名
    int rank = 1, result = 0;
    // 从全做m题开始遍历到只做1题
    for (int iterSolv = m; iterSolv > 0; --iterSolv) {
        rank += solveCount[iterSolv];
        if (a < rank && rank < b)
            result += dp[iterSolv][MaxTime];
    }
    // 若做0题，则与其他做0题的人并列排名
    if (a < rank && rank < b)
        result += dp[0][MaxTime];
    return result;
}

int main() {
    int T;
    scanf("%d", &T);
    for (int cse = 1; cse <= T; cse++) {
        init();
        read();
        printf("Case #%d: %d\n", cse, work());
    }
    return 0;
}

### C. 星界游神 llm

Problem Description

L2m 向星界游神学艺，星界游神教会他一种技能后大笑“后继有人”后溘然长逝。于是 L2m 成了新的星界游神。
L2m 比较强，可以收集红蓝绿三种调和之音。但是原本的星界游神比较弱，教给 L2m 的技能要消耗同等数量的调和之音才能发出。
Zyj 就想知道，L2m 最多能发多少次技能，好在 L2m 技能用光后打败他。

Input

第一行只有一个正整数 T （\(T\leq 1000\)），代表了 T 个情形。
接下来的 T 行，分别是三个整数 \(0<R,B,G<10^9\)，代表大佬 L2m 所拥有的红、蓝、绿三种调和之音。

Output

请你对于每种情况输出大佬能发出多少次技能。

Sample Input

1
1 3 2

Sample Output

1

解题思路

• 这是2015年广东省赛原题，我改了下题面作为签到题放上来啦。
• 因为需要消耗同等数量的调和之音，所以三个变量之间存在制约，释放技能次数取决于三者的最小值。
• 求最小值应该很好求吧，1. if-else； 2. 条件表达式(a<b)?(a<c?a:c):(b<c?b:c)； 3. 使用min函数std::min(a,b)； 4. 自己写个min函数int min(int a,int b){return a<b?a:b;}
• 时间复杂度：O(1)

#include <stdio.h>
#include <algorithm>

using std::min;

int main() {
    int T, R, B, G;
    scanf("%d", &T);
    while (~scanf("%d%d%d", &R, &B, &G)) {
        printf("%d\n", min(min(R, B), G));
    }
    return 0;
}

比赛提交代码中发现的问题

1. 交错代码了..把别的题目的代码交上来了..；
2. 又提交了exe、txt上来..；
3. 恶意提交exe，当我想打开源码看交了什么鬼时，程序卡了好久..；
4. 提交的代码中含有system("pause");，导致编译错误or超时（大概是用VC6.0写的？我建议选手们除了写作业和考试外不要使用VC6.0）；
5. 对R，G，B三个数字做奇怪的加权or除法，没看懂为什么要这么做；
6. 想将计算结果保存后再一次性输出..结果保存的还不对；还有输出漏了一个for(i=1;i<T;i++)；呃..再强调一遍，我们是可以计算完一个情形后立刻输出的；
7. 输出的时候忘记换行。你想啊，比如你要分别输出1和2，结果你输出了12，能一样吗；
8. 有选手把所有情形的答案全部加起来了才输出，啊，咋回事啊，是我的题面阅读性差嘛QAQ

### D. Oyk 剪纸

Problem Description

Oyk 又和 Zlm 剪纸了。因为以往的剪纸都是一个方向的，他们决定换个方式。
把一张矩形纸分割为 a*b 的网格，每次可以剪去 n 个格子以内组成的矩形。
Oyk 希望能剪到最后一个格子，那么他应该先剪还是后剪?

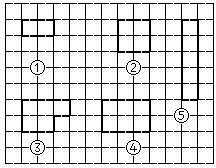
如 n=5 时，下列方案中 1,2,5 为可行方案，3 不是(因为它不是个矩形)，4 也不是(因为由 6>5 个格子组成)
注意，剪完之后如果纸断开了，可以任选一部分剪，如同它们没有断开一样，只是不可能同时剪到其中的多个部分；剪出来的部分就扔了，不再动。

Input

输入有多组（少于1000组）数据，处理到文件尾。每行有三个数字，a，b和 n（均为小于10000的正整数)，由空格隔开。

Output

对每个样例。输出 1 如果应该先走，否则输出 2。

Sample Input

1 3 1
1 3 3

Sample Output

1
1

Hint

1 3 1 中，不管剪哪一个格子，总会剩下两个，Zlm 再剪一个剩下一个，Oyk 能剪到最后一个。
1 3 3 中，Oyk 可以一次把整个纸剪了，Oyk 还是能剪到最后一个。

解题思路

• 找规律题，但我不会。于是又让Oyk教了我一次剪纸....
• Oyk：推荐先思考的经典问题：
  • 一个圆桌上放硬币，先放满（剩余空间不能再容纳）为胜，先手怎么放才能获胜；
  • 变种：一个直径d圆桌放直径p圆盘，先放满为负，问先手能不能赢；
  • 一维剪纸：一条长纸带划为n格；一条环形纸带划为n格；
• 首先观察任意大小的矩形网格纸，知道无论先手剪去哪部分，后手总能根据对称性剪去一样的部分；如果先手能够先挖掉矩形纸的中间一块，而使得剩下的纸仍然具有中心对称的性质，则获得了后手必胜局势（注意不连续的纸不能同时剪，并必须剪小矩形）。
• 由于对称性的存在，我们构造最小不同例子，分别是边长为\(1\times 1\)、\(1\times 2\)、\(2\times 2\)的矩形纸：
  • 先验证它们是最小不同例：
    1. 对于\(1\times 1\)的情况，先手总是胜。在边的两侧同时添加一行或一列不影响对称性，在边的单侧添加会由于对称性而转变为另两种情况；
    2. 对于\(1\times 2\)的情况，先手只能全部拿完才获胜。在边的两侧同时添加一行或一列不影响对称性，在边的单侧添加会由于对称性而转变为另两种情况；
    3. 对于\(2\times 2\)的情况，先手只能全部拿完才获胜。在边的两侧同时添加一行或一列不影响对称性，在边的单侧添加会由于对称性而转变为另两种情况；
    4. 不失一般性，考察\(2\times 1\)的情况，发现旋转后与\(1\times 2\)的情况等价，不需另外考虑。
  • 对于三个不同情况的等价类，边长的奇偶性相同，因此得出三种先手必胜策略：同为奇取1，同为偶取4，一奇一偶取2；
  • 显然，如果需要取的最少格子数不大于N的话，先手无法占先取得对称局势，而后手总能在第一局补齐获取对称局势所需的格子，从而获得胜利。
• 总结：根据两边长奇偶性考察N的大小。
• 时间复杂度：O(1)

参考代码

#include <stdio.h>

int main() {
    int a, b, n;
    while (~scanf("%d%d%d", &a, &b, &n))
        puts(4 >> (a % 2 + b % 2) > n ? "2" : "1");
    return 0;
}

### E. Zyj 穿越到古代

Problem Description

Zyj 又消极比赛了，这次他被 SCNU 的大佬们追杀穿越到了古代。他成了古希腊的一个将军，但是他的军队被 Hyr 带领 SCNU 的大佬们围困在山顶。眼看突破无望，但是 Zyj 军队里的将士又不肯投降,就想以死殉职。但是 Zyj 就不愿意了。他想：宝宝心里苦啊，不就是比赛的时候睡个觉嘛。于是他想出一个方法让自己逃脱制裁。
将军队里面剩下的所有人从 1 到 N 开始编号，每次数 M 个人，从 1 开始数。被数到的那个人以死殉职。然后下一个人继续从 1 开始数。Zyj 要逃脱就只能成为最后一个殉职的人，这样他就能乖乖投降了。请你告诉 Zyj 要选编号是多少才能逃脱制裁。
比如有 3 个人，编号 1,2,3。每次数 2 个，第一个殉职：2。剩下 1,3。第 2 个殉职：1。只剩下3。于是 zyj 一开始选择编号 3 可以逃脱。

Input

有多组数据，数据不超过 100 组，输入到文件尾结束。每组数据共一行两个数，第一个数 N 代表人的总数，第二个数 M 代表每次数多少个人（\(0\leq N\leq 1000\)，\(0\leq M\leq 1000000000\)）。

Output

输出一行，一个整数代表 zyj 一开始要选哪个编号才能活着。

Sample Input

5 3
4 6

Sample Output

4
3

解题思路

• 不是我出的题，只是我造的数据。数据如下：

500 999999999
500 999999797
500 999999792
500 643242600
500 123456789
491 999999999
499 999999797
503 999999792
509 643242600
521 123456789
500 1
523 1

• 可能大家都在课本上学过循环数数的方法，但这是很慢的，复杂度高达\(O(NM)\)，妥妥的TLE。
• 当然，如果你不死心，一定要模拟循环数数，那也可以的，因为只有\(N\)个人，当\(M>N\)时，数到最后一个人只会再从第一个人开始数起，不可能数出第\(M\)个人来，所以循环数数的长度应该是\(M\%N\)。时间复杂度\(O(\sum^{N}_{i=2}M\%i)=o(N^2)\)。
• 我认为我的题是必须良心的，所以放过了\(O(N^2)\)的算法，因此用一个数组标记每个人，每次你算出那个人（数组元素的下标）之后，直接把数组后面的元素往前移就相当于删掉那个人了，也就是重新标号。无论是int数组前移，还是结构体数组重标号，还是vector删除元素，都是\(O(N^2)\)的时间复杂度。
• 可惜场上没有多少同学想到要\(M\%N\)，几乎都直接循环\(M\)的长度。我真的不知道原因在哪里，是C语言课上的太水了吗？请你们在自己的电脑上测试一下，你的电脑跑\(10^9\)长度的循环需要多长时间。
• 正解：
  • 假设当前数号到\(num\)，好的他已经出局了，原来的第\(num+1\)个人成了新的第\(num\)个人；
  • 要从新的第\(num\)个人开始往后数出第\(M\)个人出局，而总人数只有\(N\)个人，所以下一次会数号到\(num'=(num+M)\%N\)，第\(num'\)个人出局，类推。
  • 因此得到一个递推公式：\(R_i=(R_{i-1}+M)\%N\)，当\(i=N\)时，总人数只剩下一个人，\(R_N\)就是Zyj想要的编号。
• 时间复杂度：\(O(N)\)

参考代码

#include <stdio.h>

int main() {
    int n, m, i, s = 0;

    while (~scanf("%d%d", &n, &m)) {
        s = 0;
        for (i = 2; i <= n; i++) {
            s = (s + m) % i;
        }
        printf("%d\n", s + 1);
    }
    return 0;
}

比赛提交代码中发现的问题

1. 跑了长度为\(M\)的循环，不再多说；
2. 以为数据还会输入一个整数\(T\)，但是这里是要读到EOF的；
3. 有同学用了链表..但是链表不能做到随机查询的话，还是模拟循环数数而已；

### F. 贪吃蛇

Problem Description

贪吃蛇是一个很有名的游戏。小蛇每吃掉一个食物,就会长长一格；撞到障碍物或自己，就会结束游戏。
这里把贪吃蛇的规则略作修改:

1. 蛇所在世界的长为 W，高为 H，坐标为左上角 (1,1) 至右下角 (W,H)。
2. 刚开始时，蛇长度为 1，位于 (1,1) 处，初始方向向东。
3. 每秒可以按下 W 表示向上，A 表示向左，S 表示向下，D 表示向右，或不按按钮，来试图对蛇进行转向，但只有试图的转向与当前方向垂直时，转向有效。
4. 每秒在尝试转向后，向新方向移动 1 格（如果转向成功）。如果吃到食物，长度增加 1，否则长度不变。
5. 世界是环形的，即从右边离开边界会从左边重新进入，以此类推
6. 撞到自己，蛇长度恢复为 1，方向、位置不变。

Input

有多组样例，处理到文件结束。每组样例第一行为三个数字 W,H,N(0<W，H<500，0<N<100000)
下面 N 行，每行：第一个字符为 WASDNwasdn 之一，字母表示那一秒的按键，N 表示那一秒不按键；大写表示吃到食物，小写表示没有。后面紧接一个空格，然后一个 64 位无符号整数\(a_i\)。

Output

对每个样例，输出一行，其值为 \(\sum_{t=1}^{N}a_t \sum_{x=1}^{W}\sum_{y=1}^{H}3^{yW+x}c_{txy} mod 2^{64}\)，其中 \(c_{txy}\) 表示第 t 秒 (x,y) 处,有蛇为 1,没有蛇为 0

Sample Input

3 2 8
a 0
s 0
D 0
N 0
n 0
w 1
s 0
n 1

Sample Output

15552

样例解释：

输出为 \(1(3^{1\times 3 + 2} + 3^{2\times 3 + 1} + 3^{2\times 3 + 2}) + 1\times 3^{1\times 3 + 2} mod 2^{64} = 9234\)

解题思路

• 模拟题。直接模拟就好，没什么特别的技巧。
• 时间复杂度：O(玄学)

参考代码（出题人的代码）

#include <stdio.h>
#include <stdlib.h>
#include <queue>
int z[500][500], q;
unsigned long long vu[300000]={1};
inline void setp(int x, int y) {
    z[x][y]=q;
}
inline void clrp(int x, int y) {
    z[x][y]=0;
}
inline bool seep(int x, int y) {
    return z[x][y]==q;
}
int main() {
    int w,h,n;
    for (n=1; n<300000; n++) {
        vu[n] = vu[n-1] * 3;
    }
    while (~scanf("%d%d%d",&w,&h,&n)) {
        char c[2];
        unsigned long long val=0, ali, map=vu[w+1];
        q++;
        int x=1, y=1, d='d';
        std::queue<int> L;
        L.push(w+1);
        while (n--) {
            scanf("%s%llu", &c, &ali);
            c[1]=c[0]<'a';
            if(c[1]) c[0]+=32;
            switch (c[0]) {
            case 'd': case 'a':
                if(d=='w' || d=='s') d=c[0]; break;
            case 'w': case 's':
                if(d=='a' || d=='d') d=c[0]; break;
            }
            switch (d) {
            case 'a':
                x--;
                if(x==0) x=w;
                break;
            case 's':
                y++;
                if(y>h) y=1;
                break;
            case 'd':
                x++;
                if(x>w) x=1;
                break;
            case 'w':
                y--;
                if(y==0) y=h;
                break;
            }
            if (c[1]) {
                //got new
            } else {
                int t=L.front()-1;
                L.pop();
                int y=t/w, x=t%w+1;
                clrp(x,y);
                map-=vu[w*y+x];
            }
            if (seep(x,y)) {
                map=0;
                q++;
                std::queue<int>t;
                std::swap(L,t);
            }
            L.push(y*w+x);
            setp(x,y);
            map+=vu[w*y+x];
            val+=ali*map;
        }
        printf ("%llu\n", val);
    }
}

### G. equation

Problem Description

给出一个各项系数均非负的多项式\(f(x)\)，是否存在\(x>0\)使得\(f(x)=1\)？

Input

每行一个样例，有多个数字（均小于25000，最多精确到6位小数）分别表示各项系数。具体地说，第\(i\)个数字表示\(f\)的\((i-1)\)次方项系数。没有列出的数字系数为0。

Output

若有解则输出解，若有多个解则从小到大输出，精确到四位小数，若无解输出空行。

Sample Input

0.5 1

Sample Output

0.5000

Hint

该输入表示\(f(x)=1x+0.5=1\)解为\(x=0.5\)

解题思路

• 二分法。
• 当各项系数非负，且\(x\geq 0\)时，\(f(x)\geq 0\)恒成立且\(f(x)\)在\([0, +\infty)\)上单调递增。
  • 如果\(\exists x>0, f(x)-1=0\)，则\(f(0)-1<0\)，即\(f(0)<1\)；
  • 考察增长最慢的一个有解函数\(f(x)=1\times 10^{-6}x=0.000001x\)（所给数据只精确到6位小数），也存在\(f(10^6)=1\)，取最近的素数\(f(10^6+3)>1\)；
  • 综上，我们可以在\((0, 10^6+3)\)区间上二分出满足\(f(x)=1\)的答案。二分精度为\(10^{-6}\)。
• 当常数项大于或等于1，则\(\forall C\geq 1, \forall x>0, f(x)=g(x)+C>1\)恒成立，此时无解。
• 当\(f(10^6+3)<1\)，说明出现比\(1\times 10^{-6}\)更小的系数，即系数全为0，此时无解。
• 时间复杂度：设\(f(x)\)最多有N项，最坏\(O(N log_2((10^6+3)\times 1/10^{-6}))=O(40N)\)

参考代码（出题人的代码）

#include <stdio.h>
#include <stdlib.h>
double g[1000007];
int n=0;
double f(double x) {
    double ans=0, leg=1;
    for (int i=0; i<n; i++) {
        ans+=g[i]*leg;
        leg*=x;
    }
    return ans;
}
int main() {
    char c;
    while (~scanf("%lf%c",g+n++,&c)) {
        if(c=='\n') {
            if (g[0]>=1 || f(1000009)<1) puts("");
            else {
                double L=0, R=1000009;
                for (; R-L>1e-6; ) {
                    double M=(L+R)*.5;
                    if (f(M)<1) L=M;
                    else R=M;
                }
                printf("%.4f\n", L);
            }
            n=0;
        }
    }
}

01/22/17更新：牛顿迭代法

由于逆天出题人二分时没有考虑精度误差，导致部分数据与实际事实不符。这里给出牛顿迭代解
注：

1. 已与Mathematica对比正确；
2. deriv()是近似求导；
3. 实际上我更倾向于迭代若干次，比如100次，而不是迭代到指定精度。

#include <stdio.h>
#include <math.h>
#include <utility>

const int MAXM = 1000003;
const double Eps = 1e-7;

int count = 0;
double coeff[1000007];

std::pair<double, double> calc(double x) {
    double func = .0, deriv = .0, p = 1.0;
    for (int i = 0; i < count; ++i) {
        double item = coeff[i] * p;
        func += item;
        deriv += i * item;
        p *= x;
    }
    return std::make_pair(func, deriv);
}

double func(double x) {
    double res = .0, p = 1.0;
    for (int i = 0; i < count; ++i) {
        res += coeff[i] * p;
        p *= x;
    }
    return res;
}

double deriv(double x) {
    return (func(x + Eps / 2.) - func(x - Eps / 2.)) / Eps;
}

inline int test() {
    return coeff[0] < 1 && func(MAXM) > 1;
}

void work2() {
    if (test()) {
        double x0 = .0, x = 1.0;
        while (fabs(x - x0) > Eps) {
            x0 = x;
            //x = x - (func(x) - 1) / deriv(x);
            std::pair<double, double> newton = calc(x);
            x = x - (newton.first - 1) / newton.second;
        }
        if (x > 0) printf("%.4f", x);
    }
    putchar('\n');
}

int main() {
/*    freopen("new_in.txt", "r+", stdin);
    freopen("new_out2.txt", "w+", stdout);*/
    char c;
    while (~scanf("%lf%c", &coeff[count++], &c)) {
        if (c != '\n') continue;
        work2();
        count = 0;
    }
    return 0;
}

### H. 续时间

Problem Description

Czj快毕业了，但他还想留在学校里，于是找到了SCNU最强大的魔法师Wwj买时间。
Wwj觉得他太蠢了，想要为难他一下，就用了分身术boom的一下变成了好多个Wwj。
Ccr经过一番侦查，发现\(N\)个Wwj的法力不一，第\(i\)个Wwj只能给Czj延长\(T_i\)的在校时间，但收费取决于心情，是心情的\(P_i\)倍，而当前Wwj的心情是\(D_i\)。
Hyr经过一番侦查，发现魔法值不一定要完全用完，比如当前Wwj收费\(C\)，Czj可以拿出\(C * a\%\)的财宝，来换取对应只有\(T_i * a\%\)的时间。
即使Czj家财万贯，天天请Lht奶茶喝，也经不住如此高昂的花费。所以他只带总共价值为M的财宝，去找Wwj的魔法分身换时间。
Lzp想知道Czj最多能延迟多长的在校时间。

Input

第一行为一个正整数\(T<50\)，代表有\(T\)种情况。
第二行输入每种情况的\(N\)和\(M\)，均是正整数，\(N\leq 1000\)，\(M\leq 10000\)。
接下来\(N\)行，每行有三个正整数，分别是\(T_i\)、\(P_i\)、\(D_i\)，均不大于\(100\)。

Output

对于每种情况，输出Czj最大能延长的时间，由题意知可能存在小数，请保留4位小数。

Sample Input

1
3 10
10 3 2
5 2 2
5 3 2

Sample Output

15

解题思路

• 我出的题都是良心题。这题是用贪心法做。我知道新生想在短时间内想出来还是挺难的，定位是中等题（什么叫难题？你看上面那两个..正常人会做的？）
• 本来我的题面是有强调 a% 的，但是我写LaTeX公式时没有对百分号 % 做转义处理，导致pdf上没显示出来，影响部分同学没看懂题，十分抱歉。
• 正解：
  1. 因为财富是一定的，所以隐含了要花最少的代价，买到最多的商品。想通了这点，你就知道应该要去计算性价比（或单价）（单价与性价比互为倒数）；
  2. 但这里的价格计算方式不一样，因为最终的花费是\(P_i\times D_i\)，所以性价比是\(\frac{T_i}{P_i\times D_i}\)；
  3. 对所有种类商品的性价比进行排序，优先买性价比最高（单价最低）的。最后由于可以买部分数量商品而不需要全买（即允许购买 a%），把剩余的钱数跟性价比一乘，就是还能买的 a% 数量的商品。
• 贪心策略证明：
  • 如果在一个可行的购买方案中，存在性价比更高的商品有剩余（没购买），那么购买该性价比更高的商品，而不够买原方案中相应总价的性价比最低商品，总能获得更多数量的商品。
  • 因此所有购买性价比最高商品的局部最优解的总和是全局最优解。

参考代码（这里采用结构体排序，并用了C++语法）

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <algorithm>

void generate() {
    FILE *outFile = freopen("in.txt", "w+", stdout);
    int T = rand() % 10 + 11;
    fprintf(outFile, "%d\n", T);
    while (T--) {
        int N = rand() % 1000 + 1;
        int M = rand() % 10000 + 1;
        fprintf(outFile, "%d %d\n", N, M);
        while (N--) {
            int Ti = rand() % 100 + 1;
            int Pi = rand() % 100 + 1;
            int Di = rand() % 100 + 1;
            fprintf(outFile, "%d %d %d\n", Ti, Pi, Di);
        }
    }
}

struct Magic {
    int T, P, D, cost;
    double ratio;

    bool operator<(const Magic &c) const {
        return fabs(ratio - c.ratio) > 1e-7 && ratio < c.ratio;
    }
} magic[1010];

int main() {/*
  generate();
  freopen("in.txt", "r+", stdin);
  freopen("out.txt", "w+", stdout);*/
    int T, N, M;
    scanf("%d", &T);
    while (T--) {
        scanf("%d%d\n", &N, &M);
        for (size_t i = 0; i < N; ++i) {
            int Ti, Pi, Di;
            scanf("%d%d%d\n", &magic[i].T, &magic[i].P, &magic[i].D);
            magic[i].cost = magic[i].P * magic[i].D;
            magic[i].ratio = (double) magic[i].T / magic[i].cost;
        }
        std::sort(magic, magic + N);
        double res = 0.;
        for (size_t i = N - 1; i >= 0; --i)
            if (M > magic[i].cost) {
                M -= magic[i].cost;
                res += magic[i].T;
            } else {
                res += M * magic[i].ratio;
                M = 0;
                break;
            }
        printf("%.4f\n", res);
    }
    return 0;
}

出题及解题总结

我校ACM吃枣药丸

建议、意见、吐槽

欢迎在下方评论区提出问题，12月内我都会回复and更新。

本文基于知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议发布，欢迎引用、转载或演绎，但是必须保留本文的署名BlackStorm以及本文链接http://www.cnblogs.com/BlackStorm/p/SCNUCPC_2016_For_Freshman_Final_Solution.html，且未经许可不能用于商业目的。如有疑问或授权协商请与我联系。