GRYZ20221020解题报告
期望得分：\(100+100+0=200 \ pts\)
实际得分：$70+100+0=170 \ pts $
题目很傻逼当然我也很傻逼。
因为赛前吸了 LB 的 rp 导致 T1 挂分（
T1 线段树
签到题。
开始以为仨操作是区间加区间推平区间求和，然后咣咣咣敲了半个小时的线段树，然后读错题，我是傻逼，然后发现维护一个 tag 就够了。
但是赛时写了个 bitset 本机跑飞快，然后发现被大样例骗了真流汗，换成 map 就过了。
/*
Knowledge : Rubbish Algorithm
Work by :Gym_nastics
Time : O(AC)
*/
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int INF=0x3f3f3f3f;
const int Mod=1e9+7;
const int N=1e7+6;
inline int read() {
int x=0,f=0;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f|=(ch=='-');
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch&15);
return f?-x:x;
}
void print(int x) {
if(x<0) putchar('-'),x=-x;
if(x>9) print(x/10);
putchar(x%10+48);
}
int n,m,Q,lazy=-1,a[N];
map<int,bool>vis;
signed main() {
// freopen("segmenttree.in","r",stdin);
// freopen("segmenttree.out","w",stdout);
n=read(),m=read();
while(m--){
int op=read();
if(op==1){
int x=read(),y=read();
if(lazy!=-1) if(!vis[x]) a[x]=lazy,vis[x]=1;
Q-=a[x];a[x]=y;Q+=a[x];
}else if(op==2){
int x=read(),y=read();
if(lazy!=-1) if(!vis[x]) a[x]=lazy,vis[x]=1;
Q-=a[x],a[x]+=y;Q+=a[x];
}else {int y=read();Q=y*n,lazy=y,vis.clear();}
print(Q),putchar('\n');
}
return 0;
}
T2 最长路
我是什么傻逼，一看这题想到了之前 LB 教我的一个二进制分组最短路，然后一分析复杂度 \(\mathcal{O(17\ n \ \log{m})}\)，好像能跑然后咣咣咣一顿乱敲最后发现还不如暴力快，然后冷静一分析发现二进制拆开之后并没有减少复杂度，并且因为分组还有了个巨大常数（
上了个厕所回来一眼看出是个拓扑，一点技术含量也没有。
#include<cmath>
#include<queue>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define int long long
using namespace std;
const int INF=0x3f3f3f3f;
const int Maxn=2e6+7;
const int Mod=1e9+7;
int read() {
int x=0,f=0;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f|=(ch=='-');
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch&15);
return f?-x:x;
}
void print(int x) {
if(x<0) putchar('-'),x=-x;
if(x>9) print(x/10);
putchar(x%10+48);
}
int n,m,f[Maxn];
int head[Maxn],cnt,Ind[Maxn];
struct node{int v,w,nxt;}e[Maxn];
void Add(int u,int v,int w){e[++cnt]=(node){v,w,head[u]},head[u]=cnt;}
queue<int>q;
signed main() {
// freopen("lpsa.in","r",stdin);
// freopen("lpsa.out","w",stdout);
n=read(),m=read();
for(int i=1;i<=m;i++){
int u=read(),v=read(),w=read();
Add(u,v,w),Ind[v]++;
}
memset(f,-INF,sizeof f);
for(int i=1;i<=n;i++) if(!Ind[i]) q.push(i),f[i]=0;
while(!q.empty()){
int u=q.front();q.pop();
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
f[v]=max(f[v],f[u]+e[i].w);
if(!(--Ind[v])) q.push(v);
}
}
int Ans=-INF;
for(int i=1;i<=n;i++) Ans=max(Ans,f[i]);
print(Ans);
return 0;
}
T3 快餐店
因为前两题太傻逼导致没时间做 T3，写完了暴力调不出来摆烂收场。
正解好像很牛逼，wapmhac 讲的也没听懂。
Konnyaku41377 深情讲解三分可是我没学（
然后看了一下就冲了。
通过样例我们大胆推测杰哥的选址一定在整点上，而 \(HLY\) 则会在边上。
所以直接 \(n^2 \log m\) 求完全源最短路直接算出杰哥的位置。
对于 \(HLY\) 的位置，我们考虑每条边 \(u,v\)，画出位置关于 \(u\) 的函数图像表示最小距离然后发现函数单峰。
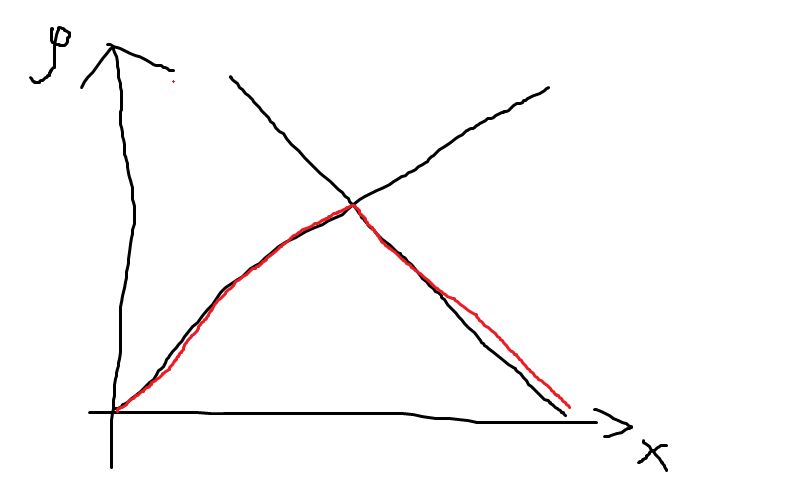
\(x\) 表示 \(HLY\) 据 \(u\) 的距离， \(y\) 表示最小距离，两条线分别表示 \(HLY\) 从 \(u\) 走还是从 \(v\) 走，然后取 \(\min\) 就行了。然后就可以套上三分，分析一下复杂度，三分是 \(O(\log_3{n})\)，然后加上枚举计算套起来是 \(O(nm \log_{3}{w})\)，大概率有问题，所以我们用随机化来控制，当然三分并非正解，需要大力吸氧（
#include<ctime>
#include<cmath>
#include<queue>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define int long long
using namespace std;
const int INF=0x3f3f3f3f;
const double eps=1e-4;
const int Maxn=1e4+3;
const int Mod=1e9+7;
int read() {
int x=0,f=0;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f|=(ch=='-');
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch&15);
return f?-x:x;
}
void print(int x) {
if(x<0) putchar('-'),x=-x;
if(x>9) print(x/10);
putchar(x%10+48);
}
int head[Maxn],cnt;
struct node{int u,v,w,nxt;}e[Maxn];
void Add(int u,int v,int w){e[++cnt]=(node){u,v,w,head[u]},head[u]=cnt;}
bool vis[Maxn];
int n,m,dis[Maxn][Maxn];
double Max=-1e18,Min=1e18;
void SPFA(int S){
typedef pair<int,int> pii;
priority_queue<pii,vector<pii>,greater<pii> >q;
memset(vis,0,sizeof vis);
for(int i=1;i<=n;i++) dis[S][i]=1e18;
q.push(make_pair(0,S));dis[S][S]=0;
while(!q.empty()){
int u=q.top().second;q.pop();
if(vis[u]) continue;vis[u]=1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(dis[S][v]>dis[S][u]+e[i].w){
dis[S][v]=dis[S][u]+e[i].w;
q.push(make_pair(dis[S][v],v));
}
}
}
double Q=0.0;
for(int i=1;i<=n;i++) Q+=1.0*dis[S][i];
Min=min(Min,Q),Max=max(Max,Q);
}
double calc(int i,double mid){
double res=0.0;
for(int i_=1;i_<=n;i_++)
res+=min(mid+1.0*dis[e[i].u][i_],1.0*(e[i].w-mid)+1.0*dis[e[i].v][i_]);
return res;
}
signed main() {
srand(time(0));
n=read(),m=read();
for(int i=1;i<=m;i++){
int u=read(),v=read(),w=read();
Add(u,v,w),Add(v,u,w);
}
for(int i=1;i<=n;i++) SPFA(i);
int T=3;
while(T--){
random_shuffle(e+1,e+cnt+1);
for(int i=1;i<=cnt;i+=2){
double l=0.0,r=e[i].w*1.0;
while(r-l>=eps){
if((double)clock()/CLOCKS_PER_SEC>1.97) break;
double lmid=l+(r-l)/3.0;
double rmid=r-(r-l)/3.0;
double resl=calc(i,lmid);
double resr=calc(i,rmid);
if(resl<=resr) l=lmid,Max=max(Max,resr);
else r=rmid,Max=max(Max,resl);
}
// if((double)clock()/CLOCKS_PER_SEC>1.97) break;
}}
printf("%.1lf %.1lf\n",Min,Max);
return 0;
}
这场直接图一乐，明天接着冲。
