拉格朗日插值
拉格朗日插值
定义:
什么是插值?
百度百科上这样写:
在离散数据的基础上补插连续函数,使得这条连续曲线通过全部给定的离散数据点。 [1]
插值是离散函数逼近的重要方法,利用它可通过函数在有限个点处的取值状况,估算出函数在其他点处的近似值。
插值:用来填充图像变换时像素之间的空隙。
人看的确信
通俗点就是李云龙拉来了一门意大利炮,然后一炮打出去,那么轨迹就可以抽象为一个函数 ,然后因为炮弹飞的很快,你能看见部分轨迹上的点,那么插值就是让你通过这些点来近似还原函数。
拉格朗日插值法
插值有很多种求法:三角函数插值,线性插值,牛顿插值,拉格朗日插值。
思想就是硬凑确信。
怎么硬凑?假设平面上有三个点,。
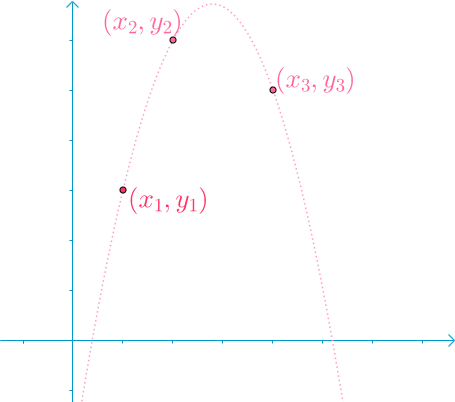
然后拉格朗日这个人呢就想对每个点搞一个子函数 ,强制令在 的时候 ,在 的时候 ,然后把这 个子函数凑起来。
那怎么计算这 个子函数?我们设第 个子函数为:
然后插值的结果就是:
现在好了,如何构造出子函数的形式呢?
因为在 时要为 ,我们可以想到令分子为 。
因为在 时要为 ,所以想到此时分子分母相同。
以 举例,那就是:
这样就满足了条件。
那么求和就是:
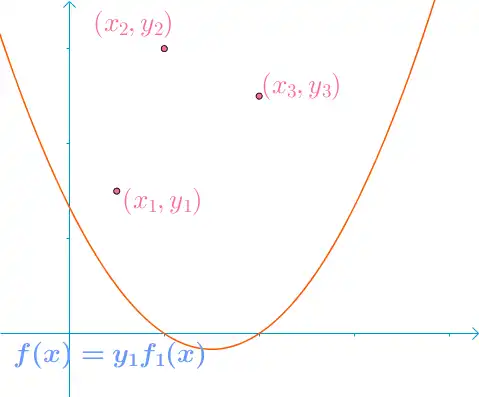
推广到一般,对于 个点,设:
那么插值结果就是:
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define debug cout<<"Szt ak ioi\n";
#define int long long
const int Mod=998244353;
const int N=1e6+7,M=2e3+1;
using namespace std;
inline int read() {
int x=0,f=0;
char ch=getchar();
while(!isdigit(ch))f|=(ch=='-'),ch=getchar();
while(isdigit(ch))x=(x<<1)+(x<<3)+(ch&15),ch=getchar();
return f?-x:x;
}
int Ans,n,k,x[N],y[N];
int inv(int a,int b){
int res=1;while(b){if(b&1) res=(res*a)%Mod;
b>>=1;a=(a*a)%Mod;}return res;
}
signed main() {
n=read(),k=read();
for(int i=1;i<=n;i++)x[i]=read(),y[i]=read();
for(int i=1;i<=n;i++){
int Fz=y[i]%Mod,Fm=1;
for(int j=1;j<=n;j++){
if(i==j) continue;
Fz=((Fz*(k-x[j]))%Mod);
Fm=((Fm*(x[i]-x[j]))%Mod);
}Ans=(Ans+(Fz*inv(Fm,Mod-2)%Mod)+Mod)%Mod;
}
printf("%lld\n",(Ans+Mod)%Mod);
return 0;
}
重心拉格朗日
咕。
本文作者:Gym_nastics
本文链接:https://www.cnblogs.com/BlackDan/p/16553363.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)