字符串算法
字符串算法
所有 NOIp 算法基本都略有了解了,唯独字符串算法一直琢磨不清楚。
于是索性写篇文章记录一下。
哈希Hash
字符串哈希
感谢 kebrantily 的博客。
给定两个字符串,判定是否相同或者查询某一字符串出现的位置或次数。
一个一个匹配太慢了,但是不知哪个睿智想到了 hash 这种东西。
原理就是把字符串转换成一个 base 进制的数。
假定一个字符串为 \(S=s_1s_2s_3…s_{len}\)
哈希函数的构造方法一般是选取两个质数 \(base \text{和} Mod\)。
或者不取模利用 unsigned long long 自然溢出。
则 \(Hash(i)={s_1 \times base^{i-1}+s_2 \times base^{i-2} + s_3 \times base^{i-3}+…+s_i \times base^{0}}\)
\(Hash(i)\) 是前 \(i\) 个字符的 \(hash\) 值。
问题,如何求一段区间 \([l,r]\) 的 \(hash\) 值。
利用 \(Hash\) 函数的构造方式,即 \(Hash_{[l,r]}=Hash_r-Hash_{l-1}\times base^{r-l+1}\)
当然要是明白一眼就能看出啥意思,想我这么笨……解释一下为什么 \(Hash_{l-1}\) 要乘一个 \(Base_{r-l+1}\),很简单,当处理到 \(Hash_{r}\) 的时候,前面 \(Hash_{l-1}\) 中的 \(s_? \times Base^{?}\) 也多乘了 \(r-l+1\) 个 \(Base\)。

形象吗?可以理解,继续。
哈希表
感谢 《一本通·提高篇》
哈希表是一种高效的数据结构。优点同字符串哈希,查找的时间几乎是 \(\mathcal{O(1)}\) 的,同时也容易实现。当然没有任何算法是完美的,其代价是较高的空间,不过随着 noip 对题目空间限制不再过多约束后,其缺点也无可厚非。
如果我们要使用一个长度为 \(n\) 的线性表,我们需要一个长度为 \(n\) 的数组,当 \(n\) 很大时,查找一个元素用二分也要 \(\mathcal{\log(n)}\),我们也可以开一个值域数组查询时可以降到\(\mathcal{O(1)}\) ,但是空间开销巨大,二者都不可取,然而哈希表融合的两者的特性,我们可以设计一个哈希函数 \(Hash(key)= key \ \bmod 13\),再令 \(A[Hash[key]]=key\)。这样数组大小开 \(12\) 就够了。
但是这同样出现一个问题,对,哈希冲突,既然选择了哈希就避免不了的出现哈希冲突。
那,可以采用邻接表的思想。实际复杂度取决于链长。
void init(){
tot=0;
while(top) adj[stk[top--]]=0;
}//初始化哈希表(多组数据时使用)
void insert(int key){
int h=key%b;//除余法
for(int e=adj[h];e;e=nxt[e])
if(num[e]==key) return;
if(!adj[h]) stk[++top]=h;
nxt[++top]=adj[h];adj[h]=tot;
num[tot]=key;
}//将一个数字 key 插入哈希表
bool query(int key){
int h=k%b;
for(int e=adj[h];e;e=nxt[e])
if(num[e]==key) return true;
return false;
}//查询数字 key 是否存在于哈希表中
出于《一本通》的代码,致敬 Kebrantily。
KMP字符串匹配
呵!乐色东西,卡我数个月都没理解。
为什么叫看猫片 KMP?
因为它有三个发明者,D.E.Knuth,J.H.Morris 和 V.R.Pratt,简称 KMP
想这么一个问题,比较两个字符串,确定其中一个为另一个的子串,怎么做?
暴力显然不可行,如果出题人卡你,每次让你在匹配最后一个字符时失配,你不得不从头匹配,复杂度退化到 \(\mathcal{O(n^2)}\)。
所以 KMP 诞生了,当文本串与模式串失配时,不必再从头开始匹配,只需要让模式串跳到,与文本串开头和文本串失配的前一个位置的具有相同前后缀的后缀的开头的位置即可(对不起语文不好请谅解),我们习惯将这个位置存到一个 \(pre\) 或 \(kmp\) 的数组里。
当然真正实现的时候没办法将模式串"挪走",只能找下标关系。
假设我们有了这么个 \(kmp\) 数组,应该如何用呢?显然的匹配成功时模式串和文本串的指针同时 \(++\) 即可。如果不匹配呢?我们只能让模式串跳到其相同的前缀去。还不匹配只能再找前缀的前缀直至能再匹配或者指针为 \(0\) 也就是得从头开始匹配了。
那我们如何求得 \(kmp\) 数组呢?我们其实已经解决了这个问题,求 \(kmp\) 数组的过程就是模式串自我匹配的过程。
根据这个,得出kmp 的代码:
/*
Knowledge : Rubbish Algorithm
Work by :Gym_nastics
Time : O(AC)
*/
#include<cmath>
#include<queue>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int INF=0x3f3f3f3f;
const int Mod=1e9+7;
const int N=1e6+6;
int read() {
int x=0,f=0;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f|=(ch=='-');
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch&15);
return f?-x:x;
}
void print(int x) {
if(x<0) putchar('-'),x=-x;
if(x>9) print(x/10);
putchar(x%10+48);
}
char s1[N],s2[N];
int len1,len2,nxt[N];
void prepare(){int j=0;
for(int i=2;i<=len2;i++){
while(j and s2[i]^s2[j+1]) j=nxt[j];
if(s2[j+1]==s2[i]) ++j;
nxt[i]=j;
}
}
signed main() {
cin>>s1+1>>s2+1;
len1=strlen(s1+1),len2=strlen(s2+1);
prepare();int j=0;
for(int i=1;i<=len1;i++){
while(j and s1[i]^s2[j+1]) j=nxt[j];
if(s1[i]==s2[j+1])++j;
if(j==len2) print(i-len2+1),putchar('\n'),j=nxt[j];
}
for(int i=1;i<=len2;i++) print(nxt[i]),putchar(' ');
return 0;
}
Trie树
为啥叫搋树啊???bing词典上Trie这个词专指字典树,emm?
准确来说,Trie 树是一种数据结构而并非算法。样子是棵树 废话,在满状态下,应该是一颗二十六叉树(只有小写字母的情况下)。就是一个节点下面有二十六个子节点,即对应的二十六个英文字母。把字典树从根节点到某一目标结点路径上字母将连成单词。
长这个样子(橙色为目标节点):

那这棵树构成的单词有 \(a,abc,bac,bbc,ca\)。
字典树的功能:
- 1.维护字符串集合
- 2.向集合中插入字符串
- 3.字符串包含问题
- 4.字符串在集合中出现次数
- 5.集合按字典序排序
- 6.求 \(LCP\)
怎么写 Trie 树?
建树过程其实和动态开点线段树一样,因为一颗二十六叉树不知道开多少,也没法表示,莫非维护二十六个变量??
void Insert(int *s,int id){ //*s相当于s[]
int pos=0,len=strlen(s); //从头开始插
for(int i=0;i<len;i++){
int ch=s[i]-'a'+1;
if(!Trie[pos].nxt[ch]) Trie[pos].nxt[ch]=++tot;//动态开点
pos=Trie[pos].nxt[ch]; //向下走
}
en[pos]=id;//标记最后一个节点为标记节点,en同时记录了是第几个单词,当然也可以只用bool记录
}
查询也大同小异,如果路径上有没标记过的点则说明单词不存在。
bool search(char *s){
int len=strlen(s),pos=0;
for(int i=0;i<len;i++){
int ch=s[i]-'a'+1;
if(!Trie[pos].nxt[ch]) return false;
}
return en[pos];
}
你完全可以用 map 水过去,但你真正练到 Trie 了吗,这里不得不反思一下做题的意义。
/*
Knowledge : Rubbish Algorithm
Work by :Gym_nastics
Time : O(AC)
*/
#include<cmath>
#include<queue>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int INF=0x3f3f3f3f;
const int Mod=1e9+7;
const int N=1e6+6;
int read() {
int x=0,f=0;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f|=(ch=='-');
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch&15);
return f?-x:x;
}
void print(int x) {
if(x<0) putchar('-'),x=-x;
if(x>9) print(x/10);
putchar(x%10+48);
}
struct node{int nxt[27];}Trie[N];
int en[N];int tot;
void Insert(char *s){
int pos=0,len=strlen(s);
for(int i=0;i<len;i++){
int ch=s[i]-'a'+1;
if(!Trie[pos].nxt[ch]) Trie[pos].nxt[ch]=++tot;
pos=Trie[pos].nxt[ch];
}
en[pos]=1;
}
int search(char *s){
int len=strlen(s),pos=0;
for(int i=0;i<len;i++){
int ch=s[i]-'a'+1;
if(!Trie[pos].nxt[ch]) return 0;
pos=Trie[pos].nxt[ch];
}
if(en[pos]==1){en[pos]++;return 1;}
return 2;
}
char ch[N];
int n,m;
signed main() {
n=read();
for(int i=1;i<=n;i++){
cin>>ch;Insert(ch);
}m=read();
for(int i=1;i<=m;i++){
cin>>ch;int res=search(ch);
if(res==1) puts("OK");
if(res==2) puts("REPEAT");
if(!res) puts("WRONG");
}
return 0;
}
AC自动机
乍一听这名字,\(AC\) 自动机?自动 \(AC\) ??同学你在想什么?对不起,这玩意只能让你自动 WA。
\(AC\) 自动机,全称 \(Aho-Corasick \ Automaton\),简称 \(AC\) 自动机。该算法在1975年产生于贝尔实验室,是著名的多模匹配算法。
单文本匹配单模式有 \(KMP\),多文本匹配单模式有 \(Trie\) 。多模式匹配,就是在一个文本串里查找多个模式串,这时候就需要 \(AC\) 自动机登场了。
前置知识:KMP 和 Trie。KMP 不要求精通但要能体会求 \(kmp\) 数组的思想,Trie 十分清楚和理解,毕竟\(AC\) 自动机是建立在 \(Trie\) 上的。
这么说,建立一个 \(AC\) 自动机需要两个步骤:
- 1.基础的 \(Trie\) 结构,将所有的模式串构成一颗 \(Trie\).
- 2.\(KMP\) 的思想,对 \(Trie\) 树上所有的节点构失配指针.
构建
关于字典树的构建,该怎么建就怎么建,但是要准确理解 \(Trie\) 中的含义。
失配指针 \(fail\)
(来自语文学困生的苦恼)
参考 \(KMP\) 的 \(kmp\) 数组的求法。\(AC\) 自动机里的 \(fail\) 数组与 \(kmp\) 数组的含义不太一样,\(fail\) 数组的意思是已匹配的后缀的对应的位置。(这句话可能不严谨,我的理解是这样的:如果我们匹配 ABCD,模式串为ABC 和 BCD,已经匹配完了ABC,发现到 D 失配了,那我们应该跳到 B 开头单词的链上找 D是否存在,然而ABC 和 BCD 存在公共的 BC 部分,如果 ABC 匹配成功了,那么BC 也一定满足了,我们只需要从失配的 C 连一条到 B 字母开头的链上的 C ,到时候直接跳过去,看看下面是不是 D 即可)
首先每个模式串的首字母肯定是指向根节点的(一个字母你瞎指什么指,指了也是头字母有什么用)
显然的 \(fail\) 指针链接的两个字母肯定相同,否则它无法作为后缀出现。
先说 \(fail\) 数组的构建:
考虑字典树中当前的结点 \(u\), \(u\) 的父结点是 \(p\),\(p\) 通过字符 c 的边指向 \(u\),即 \(Trie[p,c]=u\)。假设深度小于 \(u\) 的所有结点的 \(fail\) 指针都已求得。
-
1.如果 \(Trie[fail[p],c]\) 存在,则让 \(u\) 的 \(fail\) 指针指向 \(Trie[fail[p],c]\)。相当于在 \(p\) 和 \(fail[p]\) 后面加一个字符 \(c\),分别对应 \(u\) 和 \(fail[u]\)
-
2.如果 \(Trie[fail[p],c]\) 不存在,继续找 \(Trie[fail[fail[p]],c]\),重复 1 的判断过程,直到跳到根节点。
-
3.如果真没有,\(fail\) 指向根节点。
(摘自OI-wiki,我觉得我的语言表达不是很清楚,所以直接摘了)
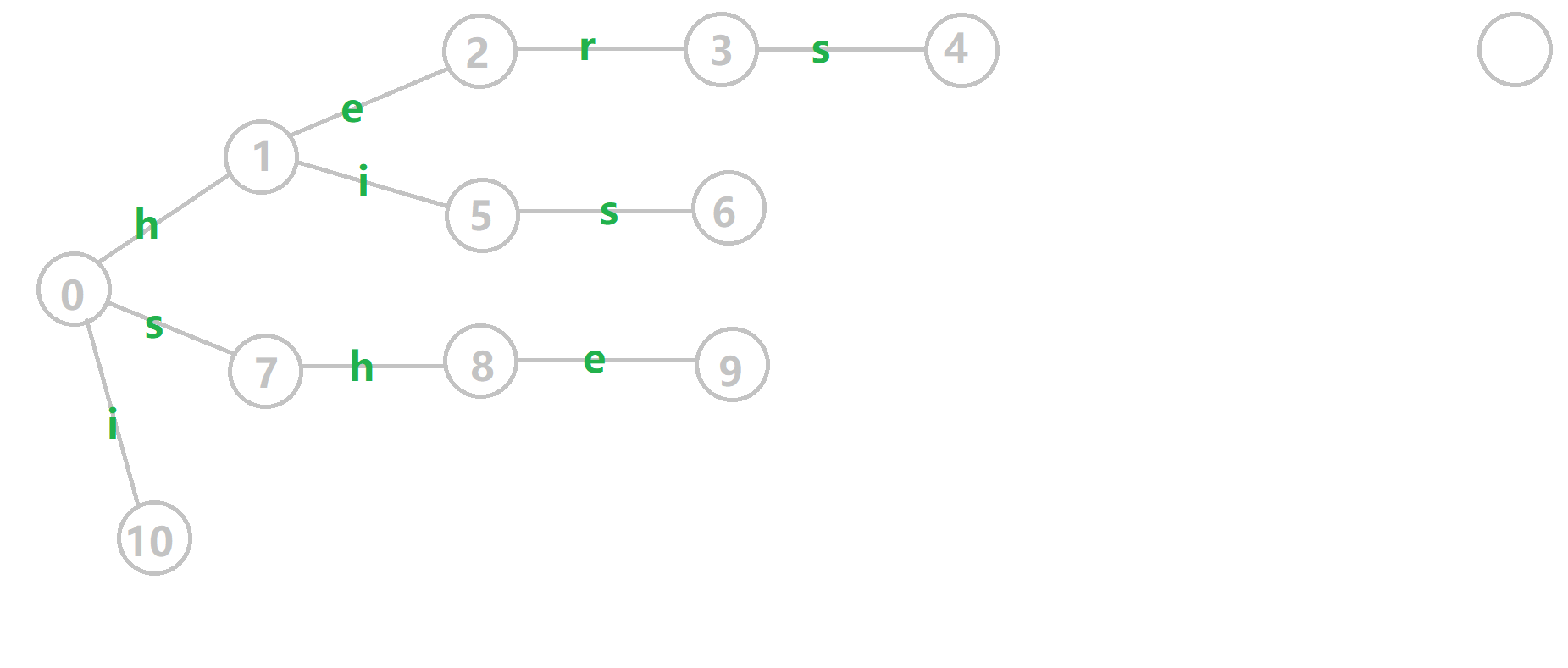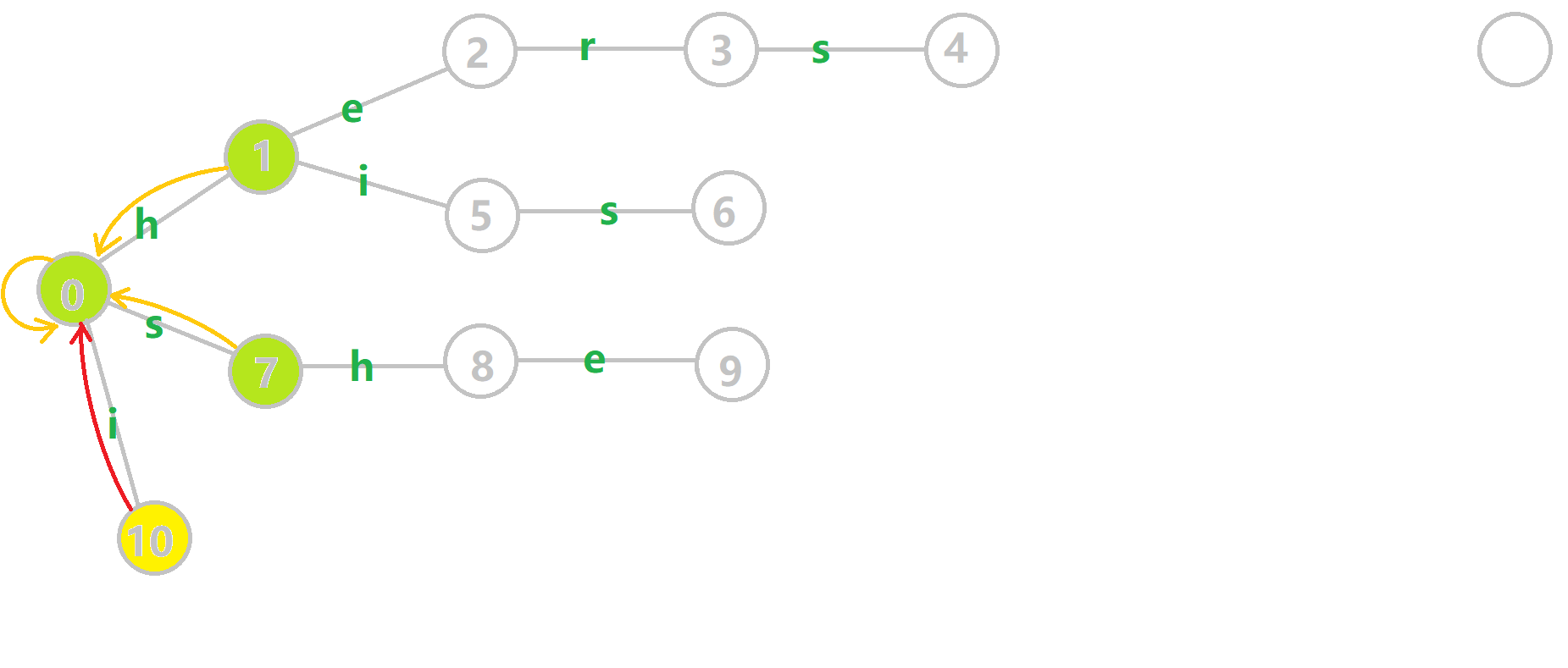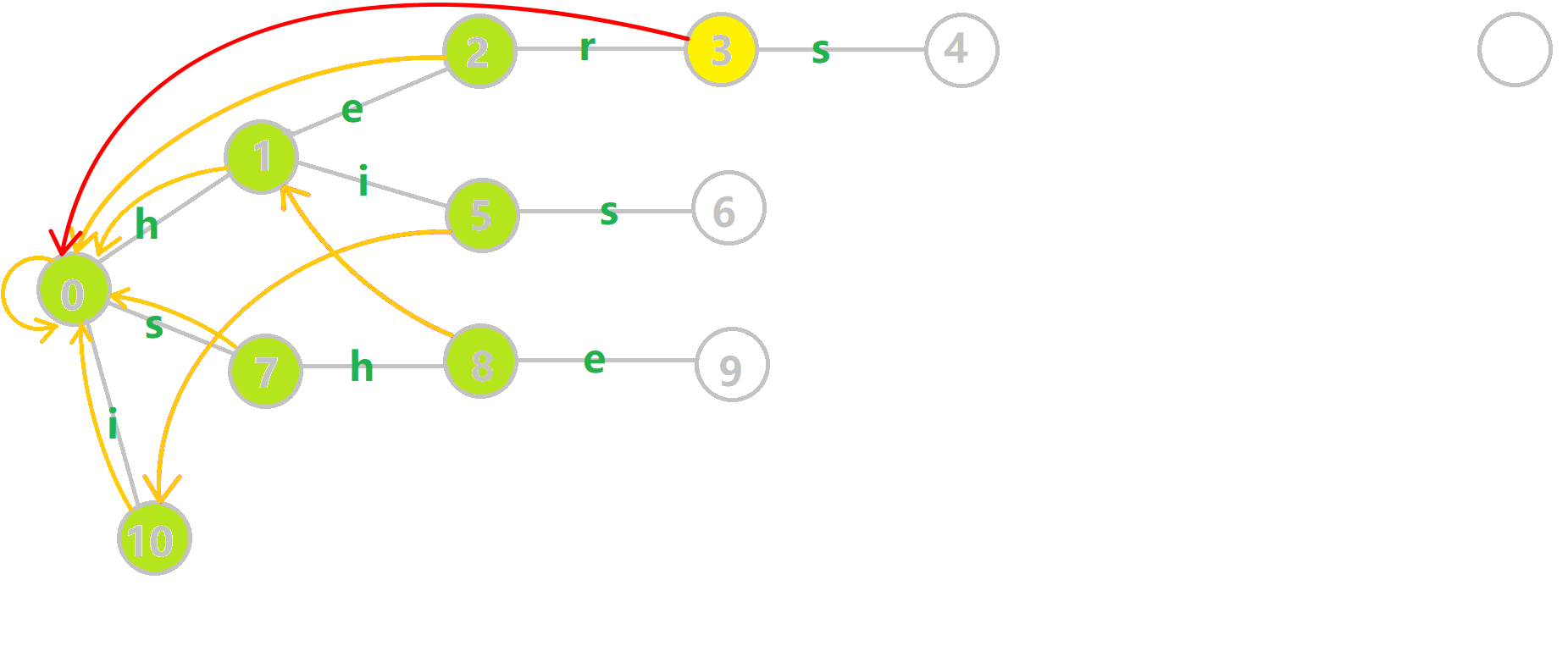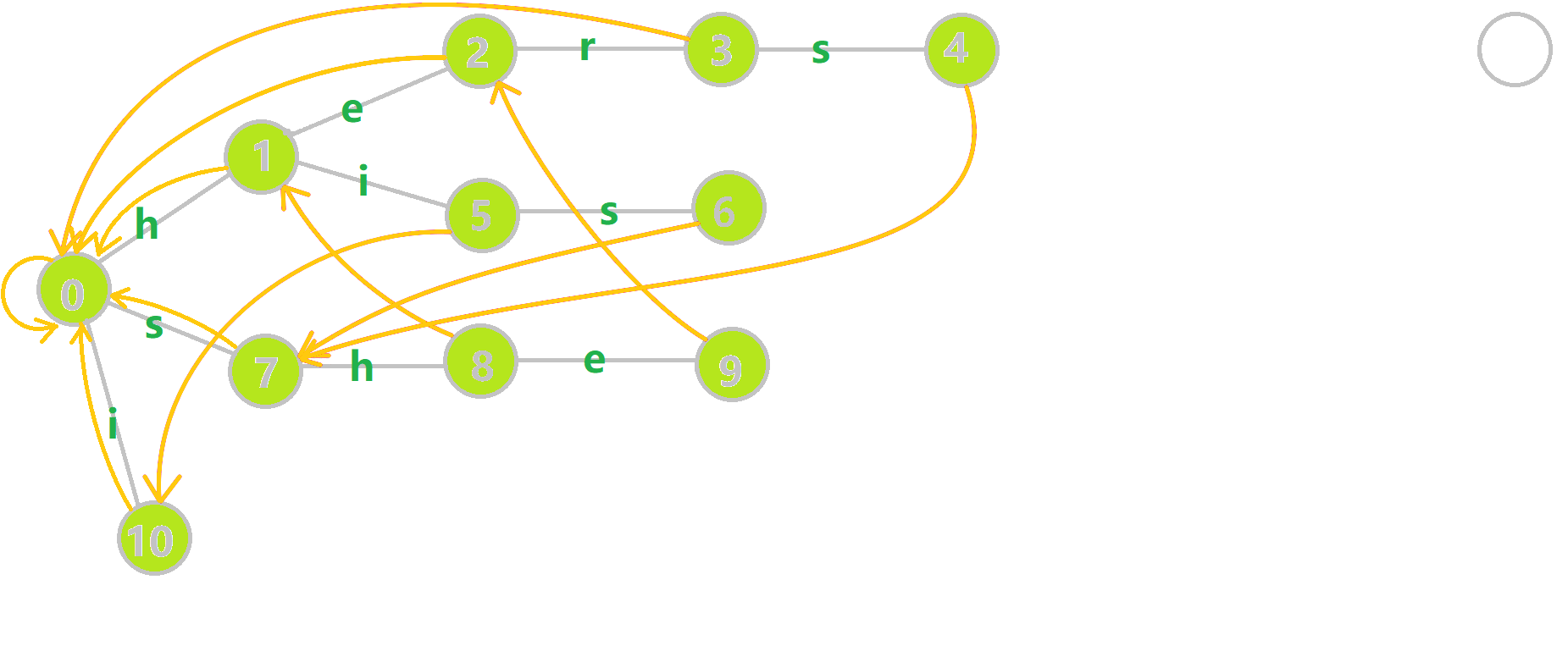
如上图,\(fail\) 指针构建过程就长这个样子。
代码也随着出来了:
void Fail() {
for(int i=1; i<=26; i++) if(Trie[0][i]) q.push(Trie[0][i]);
while(!q.empty()) {
int u=q.front();q.pop();
for(int i=1; i<=26; i++) {
if(Trie[u][i]) fail[Trie[u][i]]=Trie[fail[u]][i],q.push(Trie[u][i]);
else Trie[u][i]=Trie[fail[u]][i];
}
}
}
其中有一句话可能和你的理解有点出入,就是else Trie[u][i]=Trie[fail[u]][i],拿个图来说说:

文本串是 abcde,如果走到了 abcd 了,下一步要走 e,可是d 的下面没有了,如果不连虚拟的点,只能一步一步跳 \(fail\),最后还是跳到 \(root\) ,然后再去找 e,不如直接连一个虚拟点不用跳多次 \(fail\) ,直接一次就到了 e,注意我们是按照 BFS 的顺序来求 \(fail\) 的,所以虚点是从上到下依次连的。这就是跳转移边优化。
给出 P3808 【模板】AC 自动机(简单版)代码:
/*
Knowledge : Rubbish Algorithm
Work by :Gym_nastics
Time : O(AC)
*/
#include<cmath>
#include<queue>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int INF=0x3f3f3f3f;
const int Mod=1e9+7;
const int N=1e6+6;
int read() {
int x=0,f=0;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f|=(ch=='-');
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch&15);
return f?-x:x;
}
void print(int x) {
if(x<0) putchar('-'),x=-x;
if(x>9) print(x/10);
putchar(x%10+48);
}
int Trie[N][27],fail[N],e[N],tot,n;
queue<int>q;char s[N];
struct Algorithm{
void Insert(char *s){
int pos=0,len=strlen(s);
for(int i=0;i<len;i++){
int u=s[i]-'a'+1;
if(!Trie[pos][u]) Trie[pos][u]=++tot;
pos=Trie[pos][u];
}e[pos]++;
}
void Fail(){
for(int i=1;i<=26;i++) if(Trie[0][i]) q.push(Trie[0][i]);
while(!q.empty()){
int u=q.front();q.pop();
for(int i=1;i<=26;i++){
if(Trie[u][i]) fail[Trie[u][i]]=Trie[fail[u]][i],q.push(Trie[u][i]);
else Trie[u][i]=Trie[fail[u]][i];
}
}
}
int Query(char *s){
int pos=0,res=0,len=strlen(s);
for(int i=0;i<len;i++){
pos=Trie[pos][s[i]-'a'+1];
for(int j=pos;j&&e[j]!=-1;j=fail[j]) res+=e[j],e[j]=-1;
}return res;
}
}AC;
signed main() {
n=read();for(int i=1;i<=n;i++) cin>>s,AC.Insert(s);
cin>>s;AC.Fail();print(AC.Query(s));
return 0;
}
保证了不存在两个相同的模式串,开个 cnt 数组统计即可。
/*
Knowledge : Rubbish Algorithm
Work by :Gym_nastics
Time : O(AC)
*/
#include<cmath>
#include<queue>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int INF=0x3f3f3f3f;
const int Mod=1e9+7;
const int N=1e6+6;
int read() {
int x=0,f=0;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f|=(ch=='-');
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch&15);
return f?-x:x;
}
void print(int x) {
if(x<0) putchar('-'),x=-x;
if(x>9) print(x/10);
putchar(x%10+48);
}
int Trie[N][27],fail[N],e[N],tot,n;
queue<int>q;char s[N>>3][100],t[N];int cnt[N];
struct Algorithm{
void clear(){tot=0;
memset(Trie,0,sizeof Trie);
memset(fail,0,sizeof fail);
memset(cnt,0,sizeof cnt);
memset(e,0,sizeof e);
}
void Insert(char *s,int id){
int pos=0,len=strlen(s);
for(int i=0;i<len;i++){
int u=s[i]-'a'+1;
if(!Trie[pos][u]) Trie[pos][u]=++tot;
pos=Trie[pos][u];
}e[pos]=id;
}
void Fail(){
for(int i=1;i<=26;i++) if(Trie[0][i]) q.push(Trie[0][i]);
while(!q.empty()){
int u=q.front();q.pop();
for(int i=1;i<=26;i++){
if(Trie[u][i]) fail[Trie[u][i]]=Trie[fail[u]][i],q.push(Trie[u][i]);
else Trie[u][i]=Trie[fail[u]][i];
}
}
}
void Query(char *s){
int pos=0,res=0,len=strlen(s);
for(int i=0;i<len;i++){
pos=Trie[pos][s[i]-'a'+1];
for(int j=pos;j;j=fail[j]) ++cnt[e[j]];
}
}
}AC;
signed main() {
while(true){AC.clear();n=read();if(!n) return 0;
for(int i=1;i<=n;i++) scanf("%s",s[i]),AC.Insert(s[i],i);
scanf("%s",t);AC.Fail();AC.Query(t);int Ans=-INF;
for(int i=1;i<=n;i++) Ans=max(Ans,cnt[i]);
print(Ans);putchar('\n');
for(int i=1;i<=n;i++)if(Ans==cnt[i]) printf("%s\n",s[i]);
}
return 0;
}
这反映了什么?某些人心理之变态
/*
Knowledge : Rubbish Algorithm
Work by :Gym_nastics
Time : O(AC)
*/
#include<cmath>
#include<queue>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int INF=0x3f3f3f3f;
const int Mod=1e9+7;
const int N=1e7+6;
int read() {
int x=0,f=0;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f|=(ch=='-');
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch&15);
return f?-x:x;
}
void print(int x) {
if(x<0) putchar('-'),x=-x;
if(x>9) print(x/10);
putchar(x%10+48);
}
int Trie[N][27],fail[N],tot;
queue<int>q;int cnt[N],pre[N],n;
struct Algorithm{
void Insert(char *s,int id){
int pos=0,len=strlen(s);
for(int i=0;i<len;i++){
int u=s[i]-'a'+1;
if(!Trie[pos][u]) Trie[pos][u]=++tot;
pos=Trie[pos][u];
}pre[id]=pos;
}
void Fail(){
for(int i=1;i<=26;i++) if(Trie[0][i]) q.push(Trie[0][i]);
while(!q.empty()){
int u=q.front();q.pop();
for(int i=1;i<=26;i++){
if(Trie[u][i]) fail[Trie[u][i]]=Trie[fail[u]][i],q.push(Trie[u][i]);
else Trie[u][i]=Trie[fail[u]][i];
}
}
}
void Query(char *s){
int pos=0,len=strlen(s);
for(int i=0;i<len;i++){
pos=Trie[pos][s[i]-'a'+1];
for(int j=pos;j;j=fail[j]) cnt[j]++;
}for(int i=1;i<=n;i++) print(cnt[pre[i]]),putchar('\n');
return;
}
}AC;
char s[N];
signed main(){n=read();
for(int i=1;i<=n;i++) cin>>s,AC.Insert(s,i);
cin>>s;AC.Fail();AC.Query(s);return 0;
}
恭喜你获得了 76 分的好成绩!想一想上面这个的复杂度?
暴力去跳 \(fail\) 的最坏时间复杂度是 \(\mathcal{O(S \cdot T)}\)。为什么?因为对于每一次跳 \(fail\) 我们都只使深度减 \(1\),那样深度(深度最深的模式串长度)是多少,每一次跳的时间复杂度就是多少。那么还要乘上文本串长度,就几乎是 \(\mathcal{O(S\cdot T)}\) 的了,看数据范围,玩个锤锤。
那么加强版为什么就过了?你看题目啊,加强版的模式串长度只有 70,复杂度最坏 \(\mathcal{O(\sum70T)}\),就这还开了 \(3000ms\) 的时限。
所以怎么做?我们发现,每次跳 \(fail\) 的时候,总是由深往浅跳,所以我们把 \(u\) 到 \(fail[u]\) 连起来就是个 \(DAG\),所以,跑拓扑排序就行。
/*
Knowledge : Rubbish Algorithm
Work by :Gym_nastics
Time : O(AC)
*/
#include<cmath>
#include<queue>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int INF=0x3f3f3f3f;
const int Mod=1e9+7;
const int N=1e7+6;
int read() {
int x=0,f=0;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f|=(ch=='-');
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+(ch&15);
return f?-x:x;
}
void print(int x) {
if(x<0) putchar('-'),x=-x;
if(x>9) print(x/10);
putchar(x%10+48);
}
int Trie[N][27],fail[N],Ind[N],cnt[N],pre[N],tot,n;
char s[N];queue<int>q;
struct Algorithm{
void Insert(char *s,int id){
int pos=0,len=strlen(s);
for(int i=0;i<len;i++){
int u=s[i]-'a'+1;
if(!Trie[pos][u]) Trie[pos][u]=++tot;
pos=Trie[pos][u];
}pre[id]=pos;
}
void Fail(){
for(int i=1;i<=26;i++) if(Trie[0][i]) q.push(Trie[0][i]);
while(!q.empty()){
int u=q.front();q.pop();
for(int i=1;i<=26;i++){
if(Trie[u][i]) fail[Trie[u][i]]=Trie[fail[u]][i],q.push(Trie[u][i])
,Ind[fail[Trie[u][i]]]++;
else Trie[u][i]=Trie[fail[u]][i];
}
}
}
void Query(char *s){
int len=strlen(s),pos=0;
for(int i=0;i<len;i++){
pos=Trie[pos][s[i]-'a'+1];
cnt[pos]++;
}
}
void Toposort(){
for(int i=1;i<=tot;i++) if(!Ind[i]) q.push(i);
while(!q.empty()){
int u=q.front(),v=fail[u];q.pop();
cnt[v]+=cnt[u];if(!(--Ind[v])) q.push(v);
}
}
}AC;
signed main(){n=read();
for(int i=1;i<=n;i++) cin>>s,AC.Insert(s,i);
cin>>s;AC.Fail();AC.Query(s);AC.Toposort();
for(int i=1;i<=n;i++) print(cnt[pre[i]]),putchar('\n');
return 0;
}
没错我所有的题都是一个板子改过来的



