2022清北学堂冬 Day1 数据结构

清北澡堂搓澡记 \(Day1\)

文章中多处严重错误，请酌情思考自行改正

不是说好了讲数论吗……

分块

Q: 为什么块长\(\sqrt{n}\)？

A: 我们将序列按块大小 \(Size\) 进行分块，同时记录每块的区间和 \(sum[i]\)，显然最后一块可能不完整，但是影响不大。

• 1.查询操作：

​ \(l\) 和 \(r\) 在同一块内，暴力操作即可，最坏复杂度 \(\mathcal{O（Size）}\)

​ \(l\) 和 \(r\) 不在同一块内， 则答案会分为三部分，\(l\) 开头的不完整快，中间连续几个完整块，\(r\) 结尾的不完整块。不完整块同上，完整块直接用记录的 \(sum\) ，最坏复杂度\(\mathcal{O(\frac{n}{Size}+Size)}\)

• 2.修改操作:同查询操作。

​ 据均值不等式得，\(Size\) 为\(\sqrt{n}\) 时，复杂度最低，所以块长设置\(\sqrt{n}\) ，但是不同题目可能需要再优化。

​ 当然现在一道分块的题也没做过

树状数组

Q: 如何实现区间修改，区间查询？

​ 这个问题学树状数组的时候专门闪了，现在来证一下。

​ 我们仍和区修单查一样令\(diff[i]=a[i]-a[i-1]\)，即差分数组，更新差分数组完成区修，那区间查询怎么操作？单点查询时，我们做的是前缀和操作，同理区间查询也要前缀和，不过式子成了 \(\sum_{i=l}^{r}{\sum_{j=l}^{i}diff[j]}\)，

​ 观察式子中每个 \(diff[i]\) 的贡献，不难发现在 \(l\) 到 \(r\) 中每个 \(diff[i]\) 都贡献了\(r-l+1\) 次，所以优化后式子即： \(\sum_{i=l}^{r}(r-l+1) \cdot diff[i]\)，证毕。

线段树

扫描线求面积并

​ 这玩意可烦死了，之前学的时候就思路很不清楚，现在再复习一遍。

​ 对于每个输入信息，都代表一条线，个人喜好从下往上扫，所以扫描线是横向的，则统计每条线的 \(l\) 和 \(r\) 和 \(h\) 和是下边还是上边，同时记录出现的横坐标放入 \(x\) 数组里，按线的 \(h\) 升序排序。

​ 建树操作：线段树单点维护的不再是一个点，而是一个区间，叶子节点维护 \(x\) 数组的差值，即为区间长度，向上 \(push\_up\) 即可。

void build(int pos,int l,int r){
        tree[pos].len=X[r+1]-X[l];
        if(l==r) return; int mid=l+r>>1;
        build(lson,l,mid);build(rson,mid+1,r);
        return;
}

​ 修改操作：令 \(lazy\) 值 \(1\) 为区间有覆盖，\(0\) 为无覆盖，遇到一条线，是下边就令 \(lazy++\) ，反之为 \(--\)，因为不知道会有几个矩形覆盖。这样的话，我们就可以针对 \(lazy\) 来 \(push\_up\) ，不需要 \(push\_down\)，只要\(lazy\) 还不为零，说明这段区间仍被矩形覆盖，\(tree[pos].sum=tree[pos].len\) 即可，反之\(tree[pos].sum=tree[lson].sum+tree[rson].sum\)。

void push_up(int pos){
     if(tree[pos].lazy) tree[pos].sum=tree[pos].len;
        else tree[pos].sum=tree[lson].sum+tree[rson].sum;
}
    
void change(int pos,int l,int r,int L,int R,int k){
     if(l>=L and r<=R) {
         tree[pos].lazy+=k;
         push_up(pos);return;
      } int mid=l+r>>1;
      if(L<=mid) change(lson,l,mid,L,R,k);
      if(R>mid) change(rson,mid+1,r,L,R,k);
      push_up(pos); return;
}

​ 求并操作：既然 \(tree[pos].sum\) 维护的是覆盖宽度，那么 \(tree[1].sum\) 维护的就是两线之间的宽度和，乘上高度差即可。

 Segment::change(1,1,x-1,line[i].l,line[i].r-1,line[i].mark);
 Ans+=Segment::tree[1].sum*(line[i+1].h-line[i].h);

​ 完。

线段树求周长和

​ 咕

可持久化线段树

​ 这又是什么东西

​ 鸣谢详解主席树(可持久化线段树)-Seaway_Fu

​ 鸣谢[笔记]可持久化线段树-Luckyblock]

​ 这次Suzt_ilymtics写的什么寄吧

​ \(luckyblock\) 说得好

Q：什么时候需要持久化？

A：当你需要开一车线段树但开不下的时候。

​ 可持久化一大家子，作用是解决历史遗留问题。

​ 栗子：有一颗让某个sb人修改了 \(n\) 次的线段树，突然这个sb人问你 \(m\) 次询问之前某个节点的值，我cnmd

​ 你可能说，\(BF\) 算法分分钟爆切 \(\mathcal{O(TM\_LE)}\)，咋办，其实手画一下修改过程，貌似一大半子节点连动都没动，仔细观察一下，被更新的只有更新的那个节点到根节点链上的节点，总共 \(\log_{2}{n}\) 个节点，只更新这些节点即可。

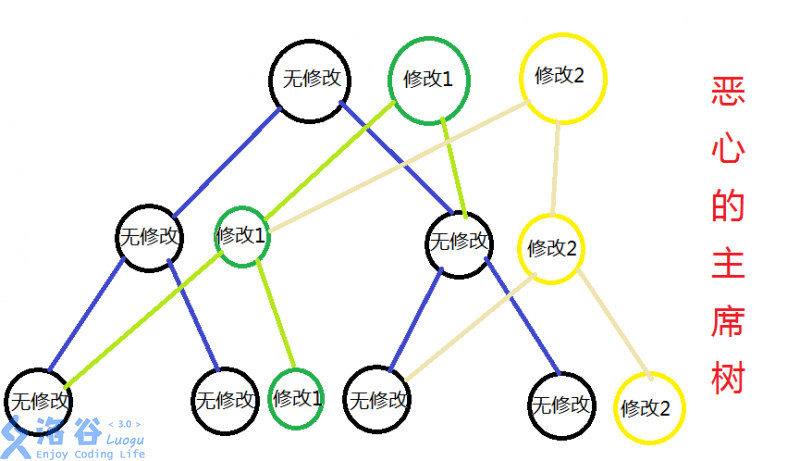
​ 这图就挺好，感性理解一手？

• 1.建树

​ 由于我们要新开节点，所以不再适用 \(pos\cdot 2\) 和 \(pos \cdot 2 + 1\) 表示左右子节点，而是要记录 \(lson\) 和 \(rson\) 的编号。

​ 那么建树操作就很好表示了。

void build(int &pos,int l,int r){
    pos=++tot;
    if(l==r){
        tree[pos].val=a[l];
        return;
    }
    int mid=l+r>>1;
    build(tree[pos].lson,l,mid);
    build(tree[pos].rson,mid+1,r);
    return;
}

​ 这里的 & 想了半天，结果发现我就是个睿智…你上面不是令每个节点都 \(++tot\) 了吗…那你每个节点不都按 \(dfs\) 序建好了吗…

• 2.可持久化修改

​ 这里有两种策略，一种是从下往上修改和新建节点，另一种是从上往下修改和新建节点，对于第一种，玩个寄吧，你又没记录父节点

​ 所以采用第二种，先建根，再向下一层一层找边建。需要开一个 \(root\) 数组记录版本数的根节点，\(root[i]\) 即表示 \(i\) 版本的节点。

int new_node(int pos){
    tree[++tot]=tree[pos];//先复制一遍节点
    return tot;//返回新节点的编号
}

int Insert(int pos,int l,int r,int x,int k){//x节点＋k
    int mid=l+r>>1;
    pos=now_node(pos);//新建pos节点
    if(l==r){
        tree[pos].val+=k;//新节点的值+k
        return pos;
    }
    if(x<=mid) tree[pos].lson=Insert(tree[pos].lson,l,mid,x,k);
    else tree[pos].rson=Insert(tree[pos].rson,mid+1,r,x,k);//分别找连在哪个位置上
    return pos;
}

​ 不理解手摸个简单的树能加深理解。

• 3.查询

​ 那就简单了吧，从给定的根节点查他就完了。

int Query(int pos,int l,int r,int x){
    int mid=l+r>>1;
    if(l==r) return tree[pos].val;
    if(x<=mid) return Query(tree[pos].lson,l,mid,x);
    else return Query(tree[pos].rson,mid+1,r,x);
}

​ \(So\) easy?

平衡树(Treap)

​ 感谢 \(zcxxxxx\) 的指导

​ 怎么还要二叉搜索树啊，又得学前置（（（

二叉搜索树(BST)

• 性质：

​ 1.左子树不为空，左子树上的点均小于根节点的值。

​ 2.右子树不为空，右子树上的点均小于根节点的值。

​ 3.左右子树也是一颗二叉搜索树。

• 功能：

​ 这玩意删除，查找，插入的复杂度都是 \(\log\) 级别的，平衡树也会用到。

​ 强就完了。

• 操作

​ 感觉整的排版怎么这么乱，下面有点多，不管排版了

​ 先说对于一个节点要记录什么？因为要不断加入删除节点，所以和主席树一样也要维护左右儿子，同时记录节点的值和这个节点值出现的次数。

   struct node{
       int val,lson,rson,cnt,Size;
   }tree[N];

​ 1.新建

​ 何时新建？当你要插入元素，但是找到该插入的位置空空如也的时候，需要把他建出来。

​ 和加边有什么区别

void new_node(int x){
    tree[++tot].cnt=tree[tot].Size=1;
    tree[tot].val=x;return;
}

​ 2.添加

​ 根据 \(BST\) 的性质，左子树都小，右子树都大，插入一个元素时，只要经过节点，那么他子树的大小肯定 \(++\)，接下来会遇到三种情况，第一种是遍历到的节点的 \(val\) 恰好等于插入的节点，\(cnt++\) 就好喽，第二种是插入的 \(val\) 比当前节点小，则进入左子树继续插入，第三种反之，但如果，插入的时候发现没有子树了，就新建他插入即可。

void Insert(int pos,int val){
    tree[pos].Size++;
    if(tree[pos].val==val){
        tree[pos].cnt++;
        return;
    }
    else if(val<tree[pos].val){
        if(tree[pos].lson) Insert(tree[pos].lson,val);
        else new_node(val);
    }
    else{
        if(tree[pos].rson) Insert(tree[pos].rson,val);
        else new_node(val);
    }
}

​ 3.删除

​ 最麻烦的一种操作，悟了好久，三种情况，本身是叶节点，直接搞掉，或者只有左子树或右子树，搞掉他，让他儿子上，最麻烦的是同时有左子树和右子树，这时候既要搞掉他，又要保持 \(BST\) 的性质，所以让他的后驱替代他即可。

int Delete_Min(int pos,int val,int res){
    if(tree[pos].val<=val){
        if(tree[pos].rson) return Delete_Min(tree[pos].rson,val,res);
        else return res; 
    }else{
        if(tree[pos].rson) return Delete_Min(tree[pos].lson,val,tree[pos].val);
        else return tree[pos].val;     
    }
}

void Delete(int &pos,int val){
    if(tree[pos].val==val){
        if(tree[pos].lson&&tree[pos].rson){
            if(tree[pos].cnt>1) tree[pos].cnt--,tree[pos].Size--;
            else tree[pos].val=Delete_Min(tree[pos].rson);
        }  
        else{
            if(tree[pos].cnt>1) tree[pos].cnt--,tree[pos].Size--;
            else pos=tree[pos].lson+tree[pos].rson;
        } 
        return;
    } 
    if(val<tree[pos].val) Delete(tree[pos].lson,val);
    else Delete(tree[pos],rson,val);
    return;
}

​ 4.查询

​ 很简单了，根据 \(BST\) 性质找就行，代码略。

Treap

\(ybt\) 云：“\(Treap\)，一种简单的平衡树，从权值上看，是一颗 \(BST\) ，从优先级上看，满足 \(priority\) ，这就是 \(Treap\) 的命名…… \(Tree\) 加 \(Heap\) 。”

为什么用 \(Treap\) ？因为如果哪个恶心出题人给你个单调的序列，\(BST\) 就会退化成链，复杂度退化为 \(\mathcal{O(n)}\) ，而随机数据使其退化的概率非常小，所以我们对 \(Treap\) 赋予的优先级采用随机数，\(Treap\) 就趋于平衡了。

上面这句话出自 \(ybt\)，好傻逼，这里看看徐爷的描述，“\(BST\) 在保证有序的情况下有很多种形状，在对 \(n\) 按 \(BST\) 排序的同时，\(rand\) 按 \(Heap\) 进行排序，树还有退化成链的可能吗？”

操作：

​ 1.\(Treap\)旋转(\(Zig\) 右旋和 \(Zag\) 左旋)

为了使 \(Treap\) 同时满足 \(BST\) 性质和小根堆性质，不可避免的对结构进行调整，调整的方式是旋转。

①左旋一颗子树，这颗子树的根节点为 \(x\) ，则旋转后会把 \(x\) 变成这个子树新根的左子节点，\(x\) 的右子节点会成为子树的新根。

②右旋一颗子树,这颗子树的根节点为 \(x\) ,则旋转后会把 \(x\) 变成这颗子树的新根的右子节点, \(x\) 的左子节点会成为子树新的跟。

显然旋转之后 \(Treap\) 仍满足 \(BST\) 的性质，长手干啥，自己画个看看。

模拟上面的过程即可。

void Zig(int &pos){
    int y=tree[pos].lson;
    tree[pos].lson=tree[y].rson;
    tree[y].rson=pos;
    tree[y].Size=tree[pos].Size;
    push_up(pos);pos=y;
    return;
}

void Zag(int &pos){
    int y=tree[pos].rson;
    tree[pos].rson=tree[y].lson;
    tree[y].lson=pos;
    tree[y].Size=tree[pos].Size;
    push_up(pos);pos=y;
    return;
}

void push_up(int &pos){
	tree[pos].Size=tree[tree[pos].lson].Size+tree[tree[pos].rson].Size+tree[pos].Size;
    return;
}

会旋了就好办了，其他操作和 \(BST\) 差不多。

​ 2. 插入：

和 \(BST\) 操作类似！

①从根节点插入。

②如果要插的值小于当前节点，进左子树。

③反之进右子树。

④如果当前节点为空，则新建节点，并为其赋一个 \(rand\) ，由于这个 \(rand\) 可能会破坏堆序，所以我们要进行一定的旋转。

⑤插入后如果左子节点的优先级小于当前节点， 右旋。

⑥反之，左旋。

void Insert(int &pos,int &val){
	if(!pos){
        pos=++tot;
        tree[pos].cnt=tree[pos].Size=1;
        tree[pos].val=val;
        tree[pos].Rand=rand();
        return;
    }
    tree[pos].Size++;
    if(tree[pos].val==val) tree[pos],cnt++;
    if(val>tree[pos].val){
        Insert(tree[pos].rson,val);
        if(tree[tree[pos].rson].Rand>tree[pos].Rand) Zag(pos);
    } else if(c<tree[pos].val){
		Insert(tree[pos].lson,val);
        if(tree[tree[pos].lson].Rand>tree[pos].rand) Zig(pos);
    }
    push_up(pos);return;
}

​ 3.删除

又是这个傻逼操作，他依然要旋转

两种情况，第一种节点为链节点或叶节点；第二种是节点同时有两个非空子节点（傻逼东西），策略是通过旋转，使节点变成可以直接删除的节点，如果左子节点优先级小于右子节点，右旋该节点，使节点降为右子树的根节点，反之左旋，继续操作，直至到能删除的节点。

void Delete(int &pos,int &val){
	if(tree[pos].val==val){
	    if(tree[pos].cnt>1) tree[pos],cnt--,tree[pos].Size--;
        else if(!tree[pos].lson||!tree[pos].rson) pos=tree[pos].lson+tree[pos].rson;
        else if(tree[tree[pos].lson].Rand<tree[tree[pos].rson].Rand) Zag(pos),Delete(pos,val);
        else Zig(pos),Delete(pos,val);
    }
    tree[pos].Size--;
    if(val>tree[pos].val) Delete(tree[pos].rson,val);
    else Delete(tree[pos].losn,val);
}

​ 4.其他

什么前驱后驱排名啊都小\(case\)了，代码不写了。

\(Splay\)

寄吧东西以后再学

后记

这金牌怕不是个ssh