树链剖分
前言
今天szt学长给我们讲了树剖,听完之后脑子着实嗡嗡的,这什么玩意啊
,本来想做题,但还是想先巩固一下吧。于是这篇文章诞生了…
树剖能干什么?
- 修改两点路径上的值
- 查询两点路径上的值
- 修改单点的值
- 查询单点的值
前置知识
1.线段树,不会请退役。
2.dfs序,不会请自行百度,这里给篇文章。
前置概念
-
1.重儿子:每个节点都会有若干个儿子节点(除叶节点),而只要这个节点不是叶子节点,它都是一棵子树的根。那么,这个父亲节点就有很多个儿子,而一定会有一个儿子的儿子最多,也就是子树最大。那么这个儿子节点就叫做\(x\)的重儿子。
-
2.轻儿子:与除重儿子外的儿子节点都是轻儿子。
-
3.重边:父节点与重儿子之间的边。
-
4.轻边:与重边相对。
-
5.重链:重边连起来的链。
-
6.轻链:轻边连起来的链。
树链剖分的预处理
这里需要两个dfs
dfs1:
预处理出每个节点的父亲,子树的大小,节点的深度以及重儿子是谁。
代码如下
void dfs1(int u,int Fa) {
Size[u]=1;fa[u]=Fa;dep[u]=dep[Fa]+1;
for(int i=head[u]; i; i=e[i].nxt) {
int v=e[i].v;if(v==Fa) continue;
dfs1(v,u); Size[u]+=Size[v];
if(Size[son[u]]<Size[v]) son[u]=v;
//如果该节点的子树大小比当前记录的重儿子的子树大小大,更新
}
}
dfs2
void dfs2(int u,int Top) {
top[u]=Top;dfn[u]=++tot;pre[tot]=u;
//top记录该链的链顶是哪个节点
//pre记录dfs序
//dfn记录节点在dfs序中的位置
if(son[u]) dfs2(son[u],Top);
//如果有重儿子先遍历重儿子所在的链。
for(int i=head[u]; i; i=e[i].nxt) {
int v=e[i].v;
if(v==fa[u] or son[u]==v) continue;
dfs2(v,v);
//非父非重儿子,即为轻链,节点和链顶都是自己。
}
return;
}
有点糊,在经szt的确认下,可以这么理解,只把重链当成一条链,轻链仅仅包含其所在的一条边。
树链剖分的操作
通过刚才的预处理,我们已经把树上节点的新编号变成了连续的。然后我们就可以针对区间(链)把原树变成线段树来进行我们要做的一系列操作。
一份线段树代码(模板题上粘的有取模请自行无视):
线段树:
namespace segment{
struct node{
int len,lazy,sum;
}tree[N<<2];
#define lson pos<<1
#define rson pos<<1|1
void build(int pos,int l,int r){
tree[pos].len=(r-l+1);
if(l==r){
tree[pos].sum=a[pre[l]]%p;
return;
}
int mid=l+r>>1;
build(lson,l,mid);build(rson,mid+1,r);
tree[pos].sum=(tree[lson].sum+tree[rson].sum)%p;
return;
}
void push_down(int pos){
if(tree[pos].lazy){
tree[lson].lazy=(tree[pos].lazy+tree[lson].lazy)%p;
tree[rson].lazy=(tree[pos].lazy+tree[rson].lazy)%p;
tree[lson].sum=(tree[lson].sum+tree[pos].lazy*tree[lson].len)%p;
tree[rson].sum=(tree[rson].sum+tree[pos].lazy*tree[rson].len)%p;
tree[pos].lazy=0;
}
return;
}
void change(int pos,int l,int r,int L,int R,int k){
if(l>=L&&r<=R){
tree[pos].sum=(tree[pos].sum+tree[pos].len*k)%p;
tree[pos].lazy+=k;
return;
} if(l>R or r< L) return;
push_down(pos);int mid=l+r>>1;
if(L<=mid) change(lson,l,mid,L,R,k);
if(R>mid) change(rson,mid+1,r,L,R,k);
tree[pos].sum=(tree[lson].sum+tree[rson].sum)%p;
return;
}
int query(int pos,int l,int r,int L,int R){
if(l>=L&&r<=R) return tree[pos].sum%p;
push_down(pos);int mid=l+r>>1,res=0;
if(L<=mid) res=(res+query(lson,l,mid,L,R)%p)%p;
if(R>mid) res=(res+query(rson,mid+1,r,L,R)%p)%p;
return res%p;
}
}
唯一的不同就在 \(build\) 当中的 $ tree[pos].sum=a[pre[l]]$ 了,意思就是pos这个点对应dfs序的点的值。
好像很绕,给个szt的图感受一下?
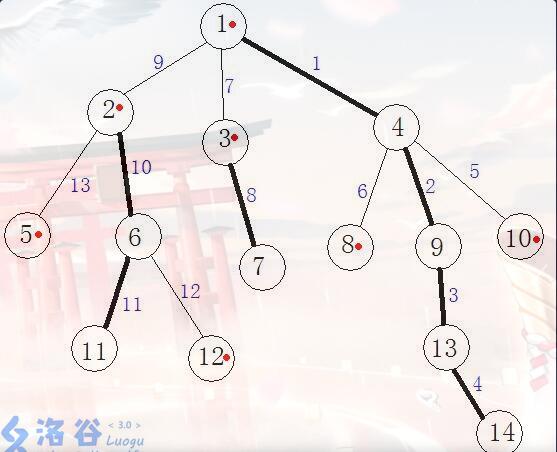
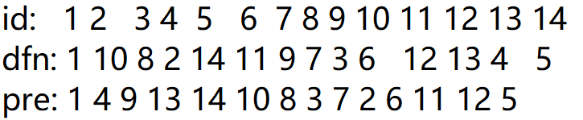
貌似可以理解,那继续。
链上修改
void change(int x,int y,int k) {
while(top[x]^top[y]){ //不断往上跳
if(dep[top[x]]<dep[top[y]]) swap(x,y); //始终保持x链的链顶的深度比y的深
segment::change(1,1,n,dfn[top[x]],dfn[x],k); // 那就将x的链顶到x修改
x=fa[top[x]]; //x向上跳
}//如果本来就在一条链上,这个while是不会执行的 ,需要下面if处理
if(dfn[x]>dfn[y]) swap(x,y); //如果在一条链上,dfs序小的肯定在上面,令x为上面的节点
segment::change(1,1,n,dfn[x],dfn[y],k);
//如果最后跳到了一个点,那这句话就是单点修改
//如果在一条链上就是修改x-y
return;
}
链上查询
与链上修改大同小异,szt就这么讲的 ,自己想一下没有问题。
int query(int x,int y) {
int res=0;
while(top[x]^top[y]) {
if(dep[top[x]]<dep[top[y]]) swap(x,y);
res=(res+segment::query(1,1,n,dfn[top[x]],dfn[x])%p)%p;
x=fa[top[x]];
}
if(dfn[x]>dfn[y]) swap(x,y);
res=(res+segment::query(1,1,n,dfn[x],dfn[y])%p)%p;
return res%p;
}



