『做题记录』[AGC028C] Min Cost Cycle
[AGC028C] Min Cost Cycle
Description
给定一个
求边权和最小的哈密顿回路的边权和。
Solution
Phase 1
首先既然是哈密顿路,那么一定会经过所有的
-
①
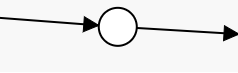
-
②
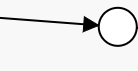
-
③

-
④

(图中的箭头表示有向边,而包含有向边的点表明该有向边的
接下来就是考虑如何把所有点拼成一个环。
首先发现②可以全部首尾相接等价地缩成一个②,③也同理。一个很显然的拼法是在全部点都是②或③的情况下,首尾相接拼成一个环,如果既有②也有③且无①、④,那么是无法拼成一个点的。考虑有①、④的情况,由于
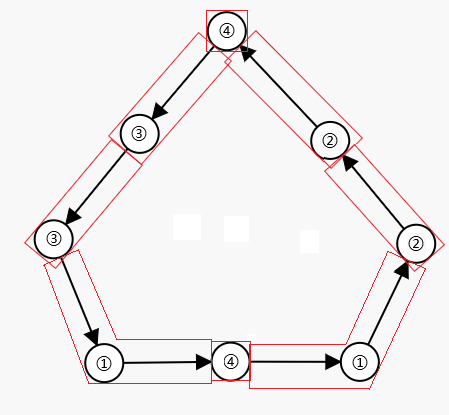
即是一种拼法。
Phase 2
我们考虑一个贪心的构造,钦定将
稍微总结一下 Phase 1 便不难得到,有且仅有一种情况是无法拼成环的,那就是每个点有各有一个
在这之后我们继续贪心地考虑,即在答案中删掉第
Code
点击查看代码
int tax[N], typ[2];
struct BLCK{LL val, id, c;}a[N];
int main() {
int n = read(), cntn = 0, flag = 0;
LL ans = 0;
rep (i, 1, n) a[++cntn] = (BLCK){read(), i, 0}, a[++cntn] = (BLCK){read(), i, 1};
sort(a+1, a+1+cntn, [&](BLCK x, BLCK y){return x.val < y.val;});
rep (i, 1, n) flag |= (++tax[a[i].id] > 1), ans += a[i].val, ++typ[a[i].c];
if (flag || max(typ[0], typ[1]) == n) return printf("%lld\n", ans), 0;
ans += a[n+1].val-a[n].val, --typ[a[n].c], ++typ[a[n+1].c];
if (a[n].id != a[n+1].id || max(typ[0], typ[1]) == n) return printf("%lld\n", ans), 0;
printf("%lld\n", min(ans-a[n+1].val+a[n+2].val, ans-a[n-1].val+a[n].val));
return 0;
}
Summary
分析问题时,可以考虑从图的性质入手,将问题的本质提炼出来,转化问题为更易求解的形式。
分类:
problems / 做题记录
标签:
做题记录



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:基于图像分类模型对图像进行分类
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 25岁的心里话
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现