『模块学习』二维计算几何基础
引言
u1s1，开这个专题未免有点太唐了……不过就像gj所说，现在学到的东西，到了大学大多能用上，那我为什么不竭尽全力学呢？
至于将“算法小记”改为“模块学习”，主要还是考虑到标题的泛用性不足，毕竟以后可能会写一些trick集合或总结（？
引入
众所周知，计算机能很好地解决代数上与图论上的问题。为了让计算机能处理几何的问题，将解析几何与线性代数的知识与计算机结合，计算几何这一学科便出现了。
计算几何在OI中考到的概率几乎没有，只是有个钟情于此的SCOI而在ACM赛场上，计算几何则是十分热门的考点，几乎每一场都会有。
本文主要是二维计算几何的基础内容，以及一些不能称之为算法、体系不那么完备的零散知识点。默认读者具有高中数学基础。
向量（重点）
向量在各种类型的问题上都具有立竿见影的效果，几乎是道计算几何题，就能题目解析中看到向量两字。同时向量也是线性代数中一个非常重要的部分，因此极为重要。
基本定义
向量
向量空间(vector space) 是形如 \((V, +, \cdot, \mathbb{P})\) 的代数系统，其中向量集合 \(V\) 与加法运算 \(+\) 组成的代数结构 \((V, +)\) 是一个 阿贝尔群(Abelian group) 。
数学与OI中提到的向量一般为 自由向量(free vector) ，其起点可任意平移，记作 \(\vec{a}\) 或 \(a\) 。在二维平面中可以用有序数对 \((x, y)\) 来表示向量。
向量相关
- 有向线段(directed line segment)： 带有方向的线段。有向线段有三要素：起点、方向、长度。这三个要素唯一确定终点，作图时一般用有向线段表示向量。
- 模(modulus)： 有向线段 \(\overrightarrow{AB}\) 的长度，即向量的 大小(magnitude) ，在数值上为 2-范数(2-norm)/欧几里得范数(Euclid norm) ，等于向量各个元素的平方和开二次根。记为 \(\left|\overrightarrow{AB}\right|\) 或 \(|a|\) 。
- 零向量(zero vector)： 模为零的向量。其方向不是固定的，记为 \(\vec{0}\) 或 \(0\) 。
- 单位向量(unit vector)： 模为 \(1\) 的向量称为该方向上的单位向量。一般即为 \(\vec{e}\) 或 \(e\) 。
- 平行向量(parallel vectors)： 方向相同或相反的两个非零向量。对于多个互相平行的向量，任意一组平行向量都可以平移到同一直线上，所以也称 共线向量(collinear vectors) 。记作 \(a\parallel b\) 。
- 相等向量(equal vectors)： 模相等且方向相同的向量。
- 相反向量(negative vectors)： 模相等且方向相反的向量。
- 向量角(vetorial angle)： 对于两个非零向量 \(a,b\) 作 \(\overrightarrow{OA} = a, \overrightarrow{OB} = b\) ，那么这两个向量的向量角就为 \(\theta = \angle AOB\) 。记作 \(\langle a, b\rangle\) 。当 \(\theta = 0\) 两向量同向， \(\theta = \pi\) 两向量反向， \(\theta = \pi/2\) 两向量 正交(orthogonal) ，并且规定 \(\theta\in[0,\pi]\) 。
基本运算
加减法
运算与物理中力的分解与合成相同，不在赘述。
具有的运算定律有交换律与结合律。
数乘
规定实数 \(\lambda\) 与向量 \(a\) 的积为一个向量，这种运算就是向量的 数乘(scalar multiplication) ，记作 \(\lambda a\) ，等于 \(\lambda\) 乘上每个向量 \(a\) 中的元素形成的新向量。
数乘的一个作用是判定两向量是否共线：两个非零向量 \(a\) 与 \(b\) 共线 \(\Leftrightarrow\) 有唯一实数 \(\lambda\) ，使得 \(b = \lambda a\) 。但实际上，叉积在计算几何中的作用完全覆盖了这点，因此数乘主要还是提供一个在空间中将向量拉伸的作用（形象理解）。
点积
点积 \(\cdot\) (dot product) 的结果是一个标量。从代数上看是两个向量对应元素乘积之和： \(\vec{a} \cdot \vec{b} = x_ax_b+y_ay_b\) 。在几何上，点积是两个向量的长度与向量角余弦的积： \(\vec{a}\cdot\vec{b} = |\vec{a}|\left|\vec{b}\right|\cos\theta\) 。
点积在计算几何中主要作用是判断方向。点积的几何意义是 \(\vec{a}\) 在 \(\vec{b}\) 所在直线上的投影与 \(\left|\vec{b}\right|\) 的乘积，反映了两个向量在方向上的相似度：\(\vec{a}\cdot\vec{b} > 0\) 则向量角在 \(0^{\circ}\) 到 \(90^{\circ}\) 之间；\(\vec{a}\cdot\vec{b} = 0\) 则两向量正交；\(\vec{a}\cdot\vec{b} < 0\) 则向量角在 \(90^{\circ}\) 到 \(180^{\circ}\) 之间。
叉乘（重点）
叉乘 \(\times\) (cross product) 的结果是一个向量。从代数角度看是 \(\vec{a}\times\vec{b} = (a_2b_3-a_3b_2, a_3b_1-a_1b_3, a_1b_2-a_2b_1)\) 。从几何角度计算为 \(\vec{a}\times\vec{b} = |\vec{a}|\left|\vec{b}\right|\sin\theta\vec{n}\) 。（其中 \(\vec{n}\) 为 \(\vec{a}\) 与 \(\vec{b}\) 所构成平面的单位向量）
通过叉乘得出的向量同时与 \(\vec{a},\vec{b}\) 正交，为这两个向量所在平面的 法向量(normal vector) 。叉乘本身是三维的，与二维本无关系，但是我们可以拓展出二维的形式，且非常有用。首先我们将三维的叉乘写成矩阵形式：
然后变换形式得到叉乘矩阵：
其中 \([a]_{\times}\) 称为 \(a\) 向量的叉乘矩阵。
得到叉乘矩阵的变换方式后，我们令 \(\vec a, \vec b\) 的第三维为 \(0\) ，得到：
最后得到的向量的第三维就是二维叉积。
值得注意的是，这个值也同时是 \(\vec a\) 与 \(\vec b\) 拼成的矩阵的行列式。在几何上，这个值的绝对值反映了 \(\vec a\) 与 \(\vec b\) 所形成的平行四边形的面积，而正负性则反映了 \(\vec a\) 到 \(\vec b\) 的旋转方向：如果 \(\vec a\times\vec b > 0\) ，那么从 \(\vec a\) 到 \(\vec b\) 为顺时针旋转；如果 \(\vec a\times\vec b > 0\) ，那么从 \(\vec a\) 到 \(\vec b\) 为顺时针旋转；如果 \(\vec a\times\vec b = 0\) ，那么 \(\vec a\) 与 \(\vec b\) 共线。
应用
判断点相对直线的位置
在计算几何中，叉积能处理非常多的问题。举个简单的例子：给定一个直线 \(l\) 与一个点 \(C\) ，如何判定点相对直线的位置？我们可以再直线上任取两点 \(AB\) ，然后将两点间线段看做一个向量 \(\overrightarrow{AB}\) ，然后从两点中任取一点，令其为 \(A\) ，与要判断的点与 \(C\) 看做向量 \(\overrightarrow{AC}\) ，利用叉积就可以判断点 \(C\) 的位置。
例题： [COCI2019-2020#2] Zvijezda
给定一个有 \(n\) 个点的凸多边形，保证 \(n\) 为偶数，对每组对边（两边之间含有 \(n/2-1\) 条边的两条边）所夹的含有凸多边形形的部分染色。然后询问 \(q\) 次，每次询问一个点 \((x_i, y_i)\) 是否在染色区。询问强制在线。
\(n, q\leq 10^5\) 。
对于这道题，由于保证了给定的一定是凸多边形，因此边按顺时针顺序斜率递减。将边编号为 \(0\sim n-1\) ，并先对 \(0\) 与 \(n/2\) 两条线判断。发现有可能有三种情况：如果在同时在两条边包含凸多边形的一边，就可以直接判定在区域内；不在任意一条边包含凸多边形的一边，那由斜率的单调性，无论怎么选边都不会使得点同时在两边含凸多边形的一边；如果仅在一条边包含凸多边形的一边，那么就利用斜率的单调性二分或倍增使另一条边达成，做不到则是不在染色区域内。
而判定这个点相对于直线的位置，使用我们上面提到的叉乘方法即可。
程序段：
点击查看代码
__int128 ccw(NODE n1, NODE n2, NODE n3) {return (__int128)(n2.x-n1.x)*(n3.y-n2.y)-(__int128)(n3.x-n2.x)*(n2.y-n1.y);}//向量叉积判顺逆
bool get(int x) {return ccw(nod[x], nod[(x+1)%n], que)>=0;}//判定是否在边x的染色区
int bins(int ql, int qr) {//二分
int L = ql, R = qr, mid;
while (L != R) {
mid = (L+R+1)>>1;
if (get(mid) == get(L)) L = mid;
else R = mid-1;
}
int ret = L-ql+1;
if (!get(ql)) ret = n/2-ret;
return ret;
}
bool check() {//处理询问
int mid = n/2, a = get(0), b = get(mid);
if (a == b) return a;
return bins(0, mid-1)+bins(mid, n-1) > mid;
}
signed main() {
int opt = read();
n = read();
for (int i = 1; i <= n; ++i) {
int x = read(), y = read();
nod.eb((NODE){x,y});
}
int q = read(), cnt = 0;
while (q--) {
int x = (read()^(opt*cnt*cnt*cnt)), y = (read()^(opt*cnt*cnt*cnt));
que = (NODE){x, y};
if (check()) ++cnt, printf("DA\n");
else printf("NE\n");
}
return 0;
}
判断两条线段是否相交
有了上面算法的基础，我们再来分析判定两条线段是否相交的问题。假设要判断的线段为 \(AB\) 与 \(CD\) ，可以先将线段 \(CD\) 看做点 \(C, D\) ，通过先前的方法判断点 \(C, D\) 是否在直线 \(AB\) 的同侧。如果在同一侧，那么 \(CD\) 必然不与 \(AB\) 相交。然后我们将 \(AB\) 拆成点，对 \(CD\) 也进行一次判断。上述过程被称作 跨立实验 ，如果两次判断都是异侧，那么我们判定这两组线段通过了跨立实验。但是注意到当两条线段共线但不相交时也可以通过跨立实验，因此想要准确判断还需要与快速排斥实验结合。
所谓 快速排斥实验 ，就是将两条线段在平面直角坐标系上扩充成矩形，然后判定这两个矩形是否相交，像这样：
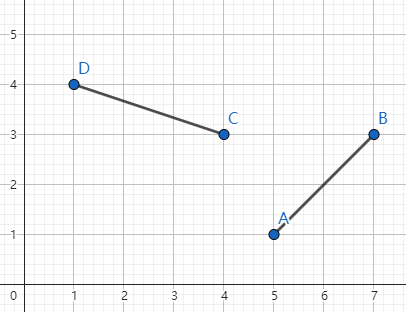
然后变为：
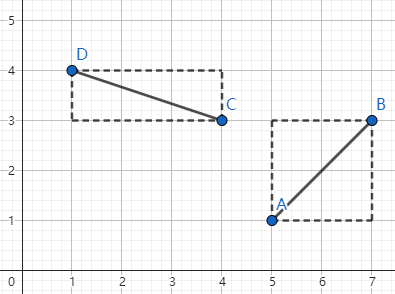
两个矩形并不相交，由此我们判定这两条线段通过了快速排斥实验。当两条线段同时通过了跨立实验与快速排斥实验，我们就判定这两条线段不相交。
平面极坐标系
我们在初中曾学过类似“在 \(A\) 点北偏东 \(30^{\circ}\) \(300\) 米” 的表述。我们发现这种位置的描述完全不同于我们平时使用的平面直角坐标系，而这就是 极坐标系(polar coordinate system) 。极坐标系在处理许多问题时具有十分优秀的性质，在计算几何中的应用较多。
坐标系的建立
- 在平面上选一定点 \(O\) ，称为 极点(polar point) ；
- 自极点引出一条射线 \(Ox\) ，称为 极轴(polar axis) ；
- 选定单位长度与角度的单位以及正方向（ 顺时针(clockwise) 或 逆时针(counterclockwise) ）
位置的描述
设我们要描述的点为 \(A\) 点。
- 极点 \(O\) 与 \(A\) 之间的距离 \(|OA|\) 称为 极径(polar radius) ，记为 \(\rho\) 。
- 以极轴为始边， \(OA\) 为终边的角 \(\angle xOA\) 称为 极角(polar radius) ，记为 \(\varphi\) 。
那么有序数对 \((\rho, \varphi)\) 即为点 \(A\) 的 极坐标(polar coordinates) 。
应用
极坐标系的应用并不是独立的，它更类似于一个脚手架，方便其他工具更好地发挥。对点按极角排序后有许多优秀的性质，这样算法的其他步骤就可以更好地解决问题。比较重要的算法有平面凸包、半平面交。下面的例题就是极坐标系与叉乘的结合。
例题： JOISC2014 K 二人の星座
平面内有 \(n(n<=3000)\) 个点，有三种颜色，每个点的颜色是三种中的一种。求不相交的三色三角形对数。
注意到两个三角形不相交，当且仅当存在一条直线使得两个三角形分别在直线的两侧。这样的直线可能有非常多，因此我们只考虑两个三角形的内公切线。朴素地运用这一点，我们可以得到一个 \(\mathcal O(n^3)\) 的算法：枚举两个点作为三角形的顶点，然后数出在直线之上与直线之下另外两种颜色的点，最后用乘法原理统计答案。
这样的复杂度还不够优秀，因此我们考虑优化算法：我们先确定一个点为极点，与 \(y\) 轴负方向平行的射线为极轴，然后按极角顺序遍历点，每访问到一个点，极点与该点相所在直线之下的点数就为极角比该点小的点数，即已遍历过的点数。这样计算的话两个三角形之间的两条公切线都会被它的两个切点统计两次，因此答案要除以 \(4\) 。时间复杂度瓶颈在与枚举极点并将其他点排序，为 \(\mathcal O(n^2\log n)\) 。
代码段：
点击查看代码
int n;
int sum[2][3], sgn[N];
struct BLCK{int x, y, c; LL px, py;}nod[N], a[N];//点的原坐标、颜色与极坐标
bool cmp(const BLCK &x, const BLCK &y) {//叉乘比较极角并排序
return x.px*y.py-x.py*y.px == 0 ? x.x < y.x : (x.px*y.py-x.py*y.px > 0)^(y.px < 0)^(x.px < 0);
}
LL ans;
void solve(int x) {//统计x为极点的贡献
memset(sum, 0, sizeof(sum));
int cntn = 0;
BLCK O = nod[x];
for (int i = 1; i <= n; ++i) if (i != x)
a[++cntn].px = nod[i].x-O.x, a[cntn].py = nod[i].y-O.y, a[cntn].c = nod[i].c;
sort(a+1, a+cntn+1, cmp);
for (int i = 1; i <= cntn; ++i) sgn[i] = (a[i].px == 0) ? 1 : abs(a[i].px)/a[i].px, ++sum[(sgn[i]+1)/2][a[i].c];
for (int i = 1; i <= cntn; ++i) {
--sum[(sgn[i]+1)/2][a[i].c];
LL tmp1 = 1, tmp2 = 1;
for (int j = 0; j <= 1; ++j)
for (int c = 0; c <= 2; ++c) {
if ((c != O.c && !j) || (c != a[i].c && j)) tmp1 *= sum[j][c];
if ((c != O.c && j) || (c != a[i].c && !j)) tmp2 *= sum[j][c];
}
ans += tmp1+tmp2;
sgn[i] *= -1;
++sum[(sgn[i]+1)/2][a[i].c];
}
}
int main() {
n = read();
for (int i = 1; i <= n; ++i)
nod[i] = (BLCK){read(), read(), read(), 0, 0};
for (int i = 1; i <= n; ++i) solve(i);//枚举极点
printf("%lld\n", ans/4);
return 0;
}
