『做题记录』[AGC032B] Balanced Neighbors

[AGC032B] Balanced Neighbors

Description

  给定整数 \(N\) ，构造一个从 \(1\) 到 \(N\) 编号的 \(N\) 个节点的无向图，使得：

• 该图不含有重边和自环，并且是连通的。
• 每个节点的所有邻接节点的编号之和相同。

  \(N \leq 100\)

Solution

  比较小巧的构造题，由于某谷上的题解过于依托，于是浅写一下。

  这道题的突破口在于找到图上不因所在节点（就是判断是否符合条件的点）变化而变化的东西，那就是图上所有点的编号和。

  想到这一点问题就迎刃而解了。考虑构造补图，对于补图而言，每个节点及其相邻点的编号和相同。用图片表示会更直观些：

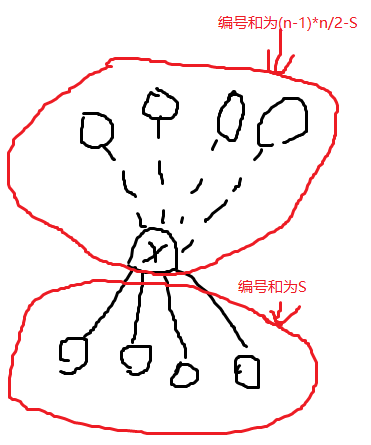
  有一种构造是对于奇数，补图分为 \(\{n\},\{1, n-1\}, \{2, n-2\}\dots\) 的连通块；对于偶数，补图分为 \(\{1， n\},\{2, n-1\}\dots\) 的连通块。由此只要构造好补图的每个连通块，输出补图即可。

Code

点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
#define mp make_pair
#define vi vector<int>
#define eb emplace_back
const int N = 1e5+5, MOD = 998244353, INF = 2e9;
inline int read() {
	register int x = 0, f = 1;
	register char ch = 0;
	while(ch < 48 || ch > 57) {
			ch = getchar();
			if (ch == '-') f = -1;
		}
	while(ch >= 48 && ch <= 57) x = x*10+(ch^48), ch = getchar();
	return f*x;
}
int main() {
	int n = read();
	if (n&1) {
		printf("%d\n", n*(n-1)/2-n/2);
		for (int i = 1; i <= n; ++i)
		for (int j = i+1; j <= n; ++j)
			if (i+j != n) printf("%d %d\n", i, j);
	}
	else {
		printf("%d\n", n*(n-1)/2-n/2);
		for (int i = 1; i <= n; ++i)
		for (int j = i+1; j <= n; ++j)
			if (i+j != n+1) printf("%d %d\n", i, j);
	}
	return 0;
}

Summary