『模块学习』SAM
引入
daduoli最近对自己的名字很感兴趣,于是他开始研究自己的名字。知周所众,搞清楚一个字符串的最好方法就是把他的所有子串列出来(误),所以daduoli开始尝试列举他名字中所有的子串。
列了好一会,daduoli发现子串太多了,于是尝试把它们拼在一起。拼了好一会儿,他拼出来一个奇怪的东西。此时shui_dream路过:“你咋拼了个SAM?”
(以上故事情节纯属虚构,如有雷同,那就雷同)
算法原理
事情还要从daduoli拼的过程说起。
daduoli打算先拿他的姓试试水(知周所众,daduoli姓daduo),他考虑将姓的所有的后缀放到一个
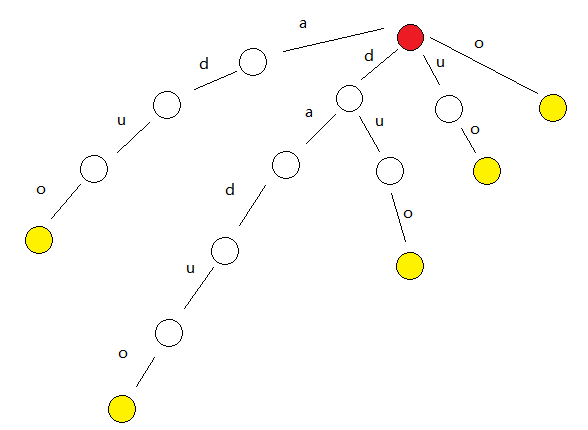
发现这个
性质1
有一个源点,若干个终止点。边代表在目前的字符串后加上的字母。从源点到任意一个节点的任意路径可以形成一个字符串
性质2
从源点到任意节点的任意路径能形成的字符串均为原串子串。从源点到任意节点的任意路径不能形成的字符串均不为原串子串(简单来说,这个图可以表示,且仅可以表示出原串的所有子串)
性质3
从源点到任意终止节点的任意路径形成的字符串均为原串后缀
性质4
从源点出发的任意两条不同路径形成的字符串不相同
虽然这个
突然,daduoli发现了这个
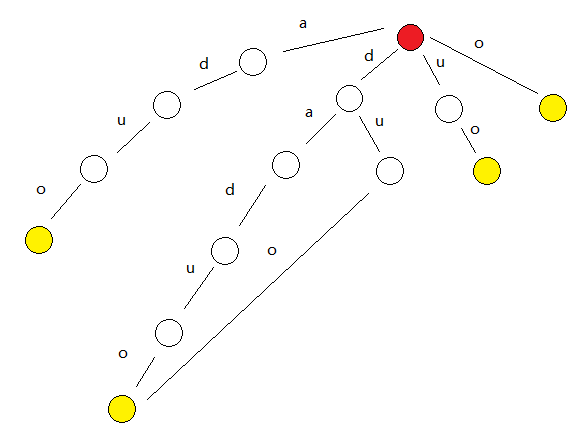
daduoli发现即使trie变成了一个DAG,他仍然能在上面找到所有的子串,于是daduoli开始思考如何把原trie压缩成一个点数尽可能少的DAG。
就在daduoli苦思冥想时,突然受到仙人托梦,醒了之后立刻就理解了一切()
接下来让我们看看daduoli理解了什么:
(daduoli觉得自己的名字真不好拼,于是下两个小节的所有图片将描述字符串"
定义
对于原串的一个子串
结论1
设两个子串中较短的串为
结论2
结论1的逆命题,分类讨论
定义:
结论3
由结论2可知,长度是连续的。并且任意的两个
后面的推论会比较重要
结论4
对于一个
发现在
由上面的两个小结论,我们就可以把“在
后缀自动机
定义:
daduoli发现可以把等价类之间的分割表示成一棵树:
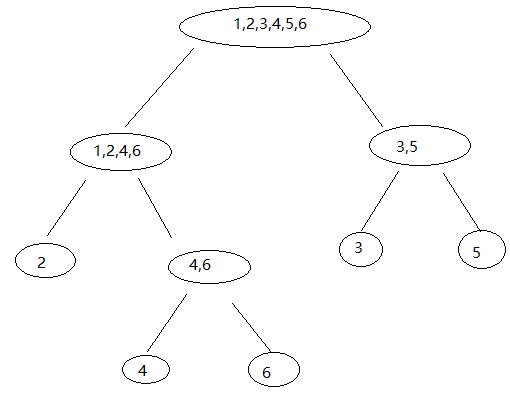
这样形成类与类之间父子关系的一棵树,就叫
结论5
其实证明早就在结论4第二个小结论的推导中便已给出。
这个结论结合结论2,我们就只需在
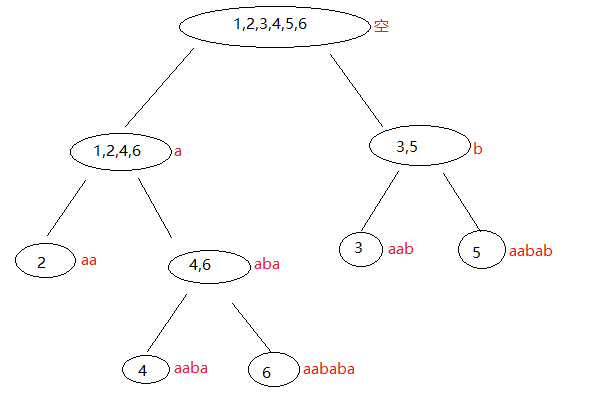
定义:后缀自动机
后文简称后缀自动机为
在daduoli坚持不懈地拼字符串后,
虽然daduoli把
(接下来是shui_dream的主场!)
shui_dream大手一挥,往daduoli的
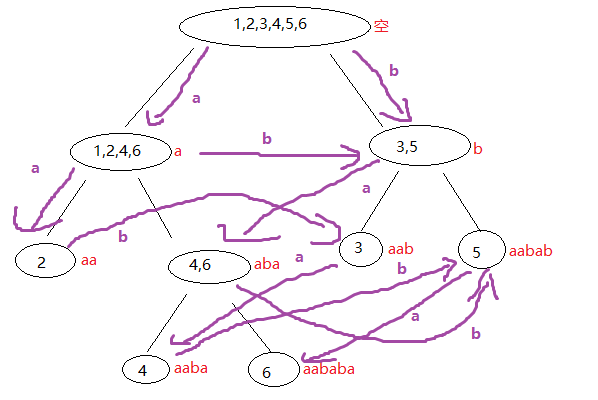
不难看出,沿着原
发现
更严谨的证明将会在后文提到,这里只是进行并不那么严谨的解释。
结论6
又臭又长,直到有这个东西就行了,先不整了
反正写代码不考证明
构造
基本形态
daduoli非常想要juan学习
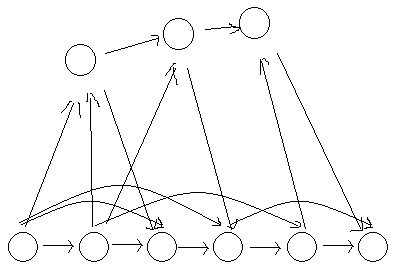
daduoli根本看不懂,于是shui_dream解释道:下面整齐的一行表示各个前缀所属的节点。一个前缀显然是所属类中长度最长的,因为它前面不能再加字符了。相邻的两个前缀显然一定会连上非树边,但是不相邻的点之间也会有边,所以这些节点放在最下面,方便观察。
上方零散的点是不包含任意前缀的类,一些边连下来,一些边连上去,内部还有一些边。这就是
Code
我相信一定有人会直接跳到这看我丑陋的马蜂的(说的就是你Cust10)
“
突然,天上掉下来一个大大的代码框和链接,想必是daduoli认真学习的样子感动了仙人吧()link:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 2e6+10; //两倍空间
struct Blck{int to, next;}e[N];
int head[N], ecnt;
void addE(int u, int v) {e[++ecnt].to = v, e[ecnt].next = head[u], head[u] = ecnt;}
struct Node {
int ch[26];
int len, fa;
}a[N];
int pre = 1, cnt = 1;
long long val[N];
void add(int x) {
int p = pre, np = pre = ++cnt; val[cnt] = 1; //新建节点
a[np].len = a[p].len+1; //新建节点
for (; p && !a[p].ch[x]; p = a[p].fa) a[p].ch[x] = np; //遍历旧串后缀连边
if (!p) a[np].fa = 1; //如果产生的都是新子串,说明是新字符,祖先连空串
else {
int q = a[p].ch[x]; //要连边的子串
if (a[q].len == a[p].len+1) a[np].fa = q; //如果满足条件,直接连q即可
else {
int nq = ++cnt; a[nq] = a[q]; //建新节点,复制出边与len
a[nq].len = a[p].len+1; //把len(nq)设为len(p)+1
a[q].fa = a[np].fa = nq; //q与np的fa都为nq
for (; p && a[p].ch[x] == q; p = a[p].fa) a[p].ch[x] = nq; //循环连边
}
}
}
long long ans;
void dfs(int x) {
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to;
dfs(y);
val[x] += val[y]; //儿子必然包含自己,因此次数加上儿子
}
if (val[x] != 1) ans = max(ans, val[x]*a[x].len); //len本身就是类中最大len的,直接乘即可
}
char str[N];
int len;
int main() {
scanf("%s", str+1);
len = strlen(str+1);
for (int i = 1; i <= len; ++i) add(str[i]-'a'); //构建SAM
for (int i = 2; i <= cnt; ++i) addE(a[i].fa, i); //邻接表储存变成真·DAG
dfs(1); //跑DAG枚举节点
printf("%lld", ans);
return 0;
}
这种题就没必要放评测记录了吧……
即使有仙人所写的精美注释,daduoli看见这玩意一脸懵逼,(我也是),于是旁边一脸轻松的shui_dream开始给daduoli一段段地讲解。
case1
int p = pre, np = pre = ++cnt;
a[np].len = a[p].len+1;
在这段程序段中,
加入了字符
注意到在加入字符
for (; p && !a[p].ch[x]; p = a[p].fa) a[p].ch[x] = np;
这个语句其实就是上述操作,去遍历每一个旧串后缀,然后尝试加上字符 p = a[p].fa 这个在 !a[p].ch[x]的意义。至于p只是为了防止自由奔放地跳出根节点。
if (!p) a[np].fa = 1;
如果说最后
case2
int q = a[p].ch[x];
if (a[np].len == a[p].len+1) a[np].fa = q;
case3
请深呼吸。
处理完这个,那么就只剩下了最后一种情况:
那么尝试解决这最后的情况。这种情况说明了存在比
那这个子串到底是什么东西呢?我们分析case2是提到过,属于
原后缀自动机中显然不存在这样一个节点包含新串结尾,因此我们新建一个节点
对于一个新的节点,我们需要考虑它的非树边怎么连,以及其在
对于
接下来考虑出边,
考虑
考虑
以上的所有步骤程序实现如下:
int nq = ++cnt; a[nq] = a[q];
a[np].len = a[p].len+1;
a[q].fa = a[np].fa = nq;
for (; p && a[p].ch[x] == q; p = a[p].fa) a[p].ch[x] = nq;
前面三行是建新节点与
Ending
最后的最后,学会了
感谢daduoli与shui_dream的友情出演()
应用
判断子串
利用第二节最开始所说的性质2即可,在
不同子串个数
字典序第
这是一个典link
Description
给定字符串
Solution
先对
然后
对于
最后输出答案则从空串开始跑,每到一个节点就与它的
Code
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 2e6+10;
struct Node {
int ch[26];
int len, fa;
}a[N];
int pre = 1, cnt = 1;
long long siz[N];
void add(int x) {
int p = pre, np = pre = ++cnt;
a[np].len = a[p].len+1; siz[np] = 1;
for (; p && !a[p].ch[x]; p = a[p].fa) a[p].ch[x] = np;
if (!p) a[np].fa = 1;
else {
int q = a[p].ch[x];
if (a[q].len == a[p].len+1) a[np].fa = q;
else {
int nq = ++cnt; a[nq] = a[q];
a[nq].len = a[p].len+1;
a[q].fa = a[np].fa = nq;
for (; p && a[p].ch[x] == q; p = a[p].fa) a[p].ch[x] = nq;
}
}
}
long long sum[N], tax[N], id[N];
void dfs(int x, int k) {
if (k <= siz[x]) return ;
k -= siz[x];
for (int i = 0; i <= 26; ++i) {
int y = a[x].ch[i]; if (!y) continue ;
if (k > sum[y]) {k -= sum[y]; continue ;}
cout << (char)(i+'a');
dfs(y, k); return ;
}
}
char str[N];
int len;
int main() {
int t, k;
scanf("%s%d%d", str+1, &t, &k);
len = strlen(str+1);
for (int i = 1; i <= len; ++i) add(str[i]-'a');
for (int i = 1; i <= cnt; ++i) ++tax[a[i].len];
for (int i = 1; i <= cnt; ++i) tax[i] += tax[i-1];
for (int i = 1; i <= cnt; ++i) id[tax[a[i].len]--] = i;
for (int i = cnt; i >= 1; --i) siz[a[id[i]].fa] += siz[id[i]];
for (int i = 1; i <= cnt; ++i) !t ? (sum[i] = siz[i] = 1) : sum[i] = siz[i];
siz[1] = sum[1] = 0;
for (int i = cnt; i >= 1; --i)
for (int j = 0; j < 26; ++j)
if (a[id[i]].ch[j]) sum[id[i]] += sum[a[id[i]].ch[j]];
// for (int i = 1; i <= cnt; ++i) printf("%lld ", sum[i]);
if (sum[1] < k) printf("-1");
else dfs(1, k);
return 0;
}
最长公共子串
广义
话说那daduoli把名字塞进
daduoli显然不会啊,于是又恭(si)恭(pi)敬(lai)敬(lian)地把shui_dream请来。shui_dream表示出强烈的兴趣,于是开始着手解决这个问题。
算法
方法1:加分隔符
shui_dream很快开始了他的思考,然而就在这时北文走了过来,看了两眼,表示:“你这歌没星号啊,那在每首歌间加星号跑普通
最怕气氛突然安静。
那么这就是第一个方法:加分隔符。但是这种方法有时候会有一定的限制,因此还是很有必要其他的广义
方法2:
咕咕咕
最后的最后,学习一下高德纳:感谢你阅读本文,希望本文对你有用。
附录:概念表
| 概念 | 含义 |
|---|---|
| 子串 |
|
| 所有 |
|
| 在等价类 |
|
| 属于 |
在等价类 |
| 旧/新串 | 增加字符 |



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:基于图像分类模型对图像进行分类
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 25岁的心里话
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现