『模块学习』网络流
网络流(network flow) 全称网络流理论,是把量类比水流的一种模型。
最大流
基础知识
对于最大流问题,其形式类似下面的例子:有一个能生产无限水的自来水厂,若干能承载无线水的节点和家三中节点,点与点之间有若干条流量有限制的单向水管,询问每时刻到家的水流量最大是多少。
在网络流中,会使用若干专有名词,其概念如下:
- 流量(flow) ,即水流量,常用 \(f\) 表示。
- 容量(capacity) ,即水管的水流量限制,常用 \(c\) 表示。
- 残量(residual) ,即容量-流量,常用 \(r\) 表示。
- 源点(source node) ,即自来水厂,常用 \(S\) 表示。
- 汇点(sink node),即家,常用 \(T\) 表示。
知道了这些以后,我们就可以用形式化的语言来阐述网络流问题:
- 反对称性 \(\space f[u \rightarrow v] = -f[v \rightarrow u]\) 。
- 内部流量守恒 对于 \(u \neq S,T\) ,流入量与流出量相等。
- 外部流量守恒 \(\sum_x f[S \rightarrow x] = \sum_y f[y \rightarrow T]\)。
- 容量限制 \(f[u \rightarrow v] \leq c[u \rightarrow v]\)。
在给定的有向图上计算出满足以上四个性质,且能使得 \(\sum_x f[x \rightarrow T]\) 最大的 \(f\) ,便是最大流问题。
问题已经很清晰了,那么如何处理呢?要解决一个大规模问题,拆分是一个重要手段。而在拆分之前,我们需要一个定理为我们的正确性提供支撑,那就是 残量调整定理 :
残量调整定理
对于网络\(c\),记所有可能的合法流的集合为 \(F_c\) 。对于任意一个 \(f \in F_c\) ,记残量网络 \(r = c - f\) ,则有 \(F_c = f + F_r\) 。用简单描述就是一个网络上的所有可能的合法流可以经由残量网络调整而来。
【证明】 对于边 \(u \rightarrow v\) 有 \(f[u \rightarrow v] = w\) ,根据反对称性有 \(f[v \rightarrow u] = -w\) ,则残量 \(r[v \rightarrow u] = c[v \rightarrow u] + w\) 。我们之后调整时可以把残量上多出来的部分给撤回去,即为每条边创造一条容量为 \(0\) 的反向边,每次正向边流量增加,反向边就增加对应的值,之后经过反向边时也同理。正向边加大流量便是加大流量,反向边增大流量相当于把正向边的流量撤回,这样便可以进行增流与撤回的操作。把所有的流都撤回去,就又变成了原网络,因此 \(F_c \leq f + F_r\) ,随后又因网络结构不变 \(F_c \geq f + F_r\) ,两者合并就是 \(F_c = f + F_r\) 。
有了这条定理,我们便有了解决问题的方法。首先我们不断寻找 增广路(augmented path) ,即残量网络 \(r\) 中,满足每条边的 \(r\) 都大于 \(0\) 的一条从 \(S\) 到 \(T\) 的路径。对于增广路也有 增广路定理 ,即当一个残量网络中不存在增广路,那么此时就是该网络的最大流。
考虑用数学归纳与反证法证明增广路定理:设当前求得的流为 \(\sum_vf[S,v]\) 且图中已不存在增广路。如果还有更大的流,那么有一个 \(f[S,v]\) 将会变大,也就意味着 \(f[v,S]\) 变小。为了 \(v\) 点流量守恒,有一个 \(f[v,u](u\neq S)\) 将会变大,那么同样的,会导致 \(f[u,v]\) 变小,需要 \(f[u,v2]\) 变大,并且 \(v2 \neq v,v2\neq S\) ,否则形成一个圈, \(v\) 点仍不满足流量守恒。以此类推,最终传递到了 \(T\) 就是一条增广路,传递不到则不满足流量守恒,由此得证。
所以,此时我们所需要做的就是找增广路一直流,知道图中不再存在增广路为止。
算法
有一种最直接的想法是从原点开始一遍遍 dfs 找增广路然后流,但如果直接使用 dfs 来暴力找增广路,那么时间复杂度将会非常地大。下面的构造能很好地说明这一点:
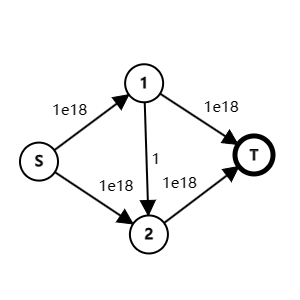
只要有合适的读边顺序, dfs 就会一直跑中间那条边与它的反边。
即使十分地显然,这种算法还是有名字的,它被称为 Ford-Fulkerson算法 。该算法的时间复杂度是 \(\mathcal{O}(m * 最大流量)\) ,即找增广路所需的 \(\mathcal{O}(m)\) 乘上找的次数。像上图一样的数据可以做到每次增广路长度为 \(1\) ,那就要找最大流量次,复杂度不是一般的大。
那么有没有办法优化一下呢?显然是有的,就是用 bfs 找增广路。
为什么 dfs 会被卡而 bfs 就不会呢?我们从bfs的性质分析:显然每次 bfs 找到的增广路一定是当前残量网络最短的一条增广路。观察之前的图可以发现 dfs 的时间复杂度亏在了中间的那条边与它的反向边上。 dfs 一直在正向边与反向边反复横跳,最后使得时间复杂度非常巨大。而 bfs 要利用反向边,必须走到一条边的尽头再往回走,而每次走最短路径的 bfs 显然是不会碰的。
这种算法被称为 Edmonds–Karp算法 ,在时间复杂度上是 \(\mathcal{O}(nm^2)\),即增广路长度 \(1 \sim n\) 的 \(n\) ,增广路找一次 \(O(m)\) ,共 \(m\) 条的 \(m^2\) 。
看起来EK已经能用了,但它还是不够优秀 Dinic算法 是对EK算法的进一步优化,先 bfs 分层限定路径,再 dfs 进行多路增广。
这样子做有什么好处呢?好处就是每一轮一定可以让增广路长度变大,一次可以跑完所有含 \(2\) 个点的路径,然后是 \(3\) 个点,最后到 \(n\) 个点。那么整个图共分 \(n\) 层,增广路不超过 \(m\) 条,增广路长度 \(1 \sim n\) ,时间复杂度就应是 \(\mathcal{O}(n^2m)\) ,把EK算法时间复杂度中的的一个 \(m\) 变成了一个 \(n\) ,在稠密图上复杂度显然是大大优于EK算法。
下面是Dinic算法的代码:
int dis[N], cur[N];
//bfs分层
bool bfs() {
rep (i, 1, cntn) cur[i] = head[i], dis[i] = INF;
queue<int> q;
q.push(S);
dis[S] = 0;
while (!q.empty()) {
int x = q.front(); q.pop();
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to;
if (dis[y] == INF && e[i].w) {
q.push(y);
dis[y] = dis[x]+1;
if (y == T) return true;
}
}
} return false;
}
//dfs增广
int dfs(int x, int flow) {
if (!flow || x == T) return flow;
int used = 0;
for (int &i = cur[x]; i; i = e[i].next) {
int y = e[i].to;
if (dis[y] != dis[x]+1) continue ;
int tmp = dfs(y, min(flow-used, e[i].w));
if (tmp) {
e[i].w -= tmp, e[i^1].w += tmp;
used += tmp;
if (used == flow) return flow;
}
} return used;
}
int dinic() {int ret = 0; while (bfs()) ret += dfs(S, INF); return ret;}
基本应用
二分图相关
网络流与二分图的关系非常密切,一个很基本的建模思想是将源点与二分图的一部分点连容量为 \(1\) 的边,将另一部分点与汇点连容量为 \(1\) 的边,原图上的边则直接连上容量为 \(1\) 的边。这样跑最大流就相当于在选择边,最终得到的就是这个二分图的最大匹配。实际应用时,需要灵活的在这个模型的基础上变换。
最大流最小割定理
这是最大流中的一个重要的定理,它的内容十分简单: 一个图的最大流 = 最小割 。
所谓 割(cut) ,就是一个边集,能够通过删掉集合中所有的边来使得图中的点分成不联通的两部分。而最小割就是使得集合中所有边容量之和最小的割。
要证明该定理,我们考虑将该定理分为两个部分: 最大流 \(\leq\) 最小割 与 最大流 \(\geq\) 最小割 。由割的定义可知,最大流中的每一条流一定经过割边集中的一条边,那么流量和的最大值不可能超过割边集中边的容量和;一个最大流中,满流的边分布一定成为一个割,否则就还能继续增广。由此,我们便证明了最大流最小割定理。
在实际应用中,最小割问题的出现不比最大流问题少,而通过最大流最小割问题,就能方便地求取最小割,对解决问题的帮助不可谓不大。
进阶应用
最小路径覆盖问题
例题:洛谷P2765 魔术球问题
假设有 \(n\) 根柱子,现要在这 \(n\) 根柱子的中依次放入编号为 \(1,2,3,\cdots\) 的球,要求每次放的球要放在所放柱子的最上方,并且同一根柱子中所有上下相邻的两个数之和为完全平方数。
求 \(n\) 根柱子最多放多少球。
不难发现,本题的关键在于数与数之间的关系。我们考虑将满足两两相加为完全平方数的两个点之间连上边,构造出一个图:
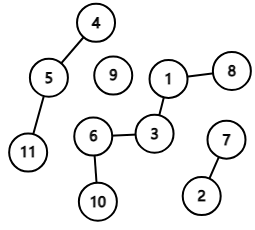
这样一来问题就变成了在图上用 \(n\) 条路径最多能覆盖多少从 \(1\) 开始编号连续的点。不难发现答案是单调的,如果 \(1\sim x\) 点构成的图最少需要用 \(y\) 条路径覆盖,那么覆盖 \(1\sim x+1\) 所需的路径条数一定是 \(y\) (能接在前一个图的最优方案的一条覆盖路径上)或 \(y+1\) (必须使用一条新路径来覆盖)。于是我们可以从 \(1\) 开始这一条件可以通过按顺序逐步往图中加入点。由于可以在原来已经跑过最大流算法的残量网络上加边建图再跑,所以复杂度上是不会有问题的。那么最后我们将问题变为了对于一个图,判断其是否能使用 \(n\) 条路径覆盖。
最后要解决的这个问题叫做 最小路径覆盖问题 ,可以使用最大流算法来解决。考虑先把图的每一个点都用一条只覆盖该点的路径覆盖,最后将路径一条条合并,我们想要合并的次数最多,那么我们可以使用最大流来计算:我们先用拆点的思想,把每个点分成入点和出点,并且从原点出发向所有出点连一条容量为 \(1\) 的边,从所有出点出发向汇点连一条容量为 \(1\) 的边。所有如果两个数相加等于完全平方数,那么我们就从较小数的出点向较大数的入点连一条容量为 \(1\) 的边。每一条经过点 \(x,y'\) 的流都相当于合并以 \(x\) 为一端的路径与 \(y\) 为一端的路径。由此点数减最大流就是我们要求的路径数。
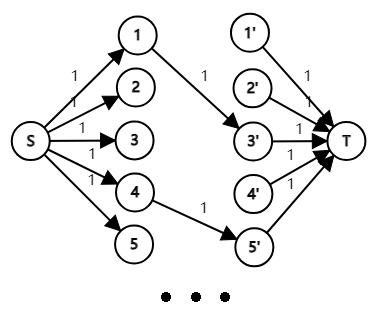
下面是建图部分的程序段:
int main() {
int n = read(); S = 1, cntn = T = S+1;
//不断建图
while ((cntn-2)/2-sum <= n) {
cntn += 2;
int num = (cntn-2)>>1, sq;
addE(S, cntn-1, 1), addE(cntn, T, 1);
rep (i, 1, num-1) {
sq = sqrt(i+num);
if (sq*sq == i+num) addE(num*2+1, i*2+2, 1);
}
int tmp = 0;
while (bfs()) tmp += dfs(S, INF);
sum += tmp;
}
printf("%d\n", (cntn-2)/2-1);
for (int i = 2; i <= cnte; i += 2)
if (!e[i].w && e[i].u != S && e[i].to != T) tt[(e[i].u-1)/2] = (e[i].to-2)/2, pp[(e[i].to-2)/2] = (e[i].u-1)/2;
rep (i, 1, (cntn-2)/2-1) {
if (!pp[i]) {
printf("%d ", i);
int p = i;
while (tt[p]) printf("%d ", tt[p]), p = tt[p];
puts("");
}
}
return 0;
}
最大权闭合子图问题
例题:洛谷P2762 太空飞行计划问题
给定含 \(m\) 个实验的实验集合 \(E = \{E_1,E_2,\cdots, E_m\}\) ,以及含 \(n\) 个仪器的仪器集合 \(I = \{I_1, I_2,\cdots, I_n\}\) 。对于一个实验 \(E_i\) ,完成该实验所需的设备集合是 \(I\) 的一个子集 \(R_i\) ,并且完成该实验会获得 \(p_i\) 元。对于设备 \(I_i\) 购买该设备所需的费用为 \(c_i\) 。
初始资金足够买下所有设备,求最大净收益。
我们可以将题目抽象为这样 最大权闭合子图 的模型:有若干点,每个点有一个权值,并且有一些有向边。可以选出一个 闭合子图(即子图中所有点的出边都被包含,且出边所指的点在子图中),使得子图中点的权值总和最大。
我们考虑将最大权变成最小割,因为最小割与选择十分契合,只要把点权转化为边权即可。我们知道,权值和 \(=\) 所有正权点权值和 \(-\) 不在所选闭合子图中正权点权值和 \(+\) 在所选子图中负权点权值和。要求得最大的权值和,那么就是要该式子的后两项尽可能的小。那么接下来就是将后面这两项转化为最小割。
考虑这样的建图方式:首先从源点向所有权值为正的点连边,边权为点的权值;然后将原图上所有的点在新图上连接,边权为 \(\infty\) ,因为我们不希望这些边被选,这样设置权值可以让最小割不包含这些边;最后将负权点向汇点连边,容量为负权点的权值绝对值。
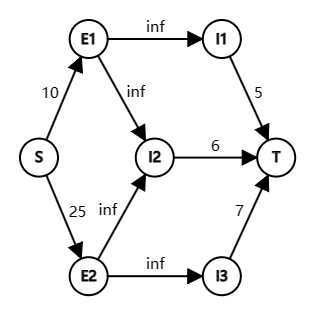
下面来验证这个模型的正确性:因为割将图分为两个部分,且与源点相连的部分必然没有其他出边,所以它必然对应着原图的一个闭合子图。中间的边是必然不会被选的,而正权点的边被割掉就意味着不选该正权点,负权点的边被割掉就意味着选择该负权点。这样一来,我们就将答案转换为了最小割,而根据最大流最小割定理,我们是可以通过最大流算法来求解的。
程序段:
int main() {
int n = read(), m = read(); S = n+m+1, cntn = T = S+1;
//建图
rep (i, 1, n) {
int w = read(), v;
sum += w;
addE(S, i, w);
while (1) {
int x = 0, f = 1, flag = 0;
char ch = 0;
while(ch < 48 || ch > 57) {
ch = getchar();
if (ch == '-') f = -1;
if (ch == '\n') {flag = 1; break;}
}
if (flag) break;
while(ch >= 48 && ch <= 57) x = x*10+(ch^48), ch = getchar();
v = f*x;
addE(i, v+n, INF);
if (ch == '\n') break;
}
}
rep (i, 1, m) addE(i+n, T, read());
//最小割
int ret = dinic();
//输出方案及答案
rep (i, 1, n) {
if (dis[i] != INF) printf("%d ", i);
} puts("");
rep (i, 1, m) {
if (dis[i+n] != INF) printf("%d ", i);
} puts("");
printf("%d\n", sum-ret);
return 0;
}
最小费用最大流
基础知识
最小费用最大流,顾名思义,就是给边增添了第二个属性——费用,表示每在该边流过 \(1\) 单位的流量,就需要消耗的费用。而最小费用最大流,就是找出所需费用最小的最大流。
算法
贪心地,我们会想在增广时找费用最小的增广路增广,而这恰巧就是正确的!该算法被称为 SSP(Successive Shortest Path)算法 ,能够处理无负环网络的最小费用最大流。下面我们来证明其正确性。
仍然是反证法:我们设 \(f_i\) 表示流量为 \(i\) 时的最小费用。自然地,如果网络上没有负圈,那么 \(f_0 = 0\) 。在 \(f_i\) 的基础上,找到一条最短的的增广路,求出 \(f_{i+1}\) 。此时 \(f_{i+1}-f_i\) 是这条增广路的长度。
根据反证法,那么此时存在一个比 \(f_{i+1}\) 更小的 \(f_{i+1}'\) 。因为我们找到的增广路是最短的,因此 \(f_{i+1}'-f_i\) 只能对应着一条含负环的路径。此时,这个结果就与 \(f_i\) 为最小费用的假设就出现了矛盾:只要在负环上增加流量,那么就可以在总流量不变的情况下,使得 \(f_i\) 对应的费用变小。
由此,SSP算法可以正确求解无负环网络的最小费用最大流。如果要用该算法处理含负环的费用流问题,应先使用消负环的算法处理一遍。
SSP算法的实现并不麻烦,只要将最大流算法中寻找增广路的过程替换为求单位费用最小的最短路算法即可。下面给出基于Dinic算法的代码实现:
int dis[N], cur[N];
bool vis[N];
bool spfa() {
for (int i = 1; i <= cntn; ++i) dis[i] = INF, cur[i] = head[i];
queue<int> q;
q.push(S);
dis[S] = 0;
vis[S] = 1;
while (!q.empty()) {
int x = q.front(); q.pop(), vis[x] = 0;
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to;
if (dis[y] > dis[x]+e[i].c && e[i].w) {
dis[y] = dis[x]+e[i].c;
if (!vis[y]) {
q.push(y);
vis[y] = 1;
}
}
}
} return dis[T] != INF;
}
int dfs(int x, int flow) {
if (x == T || !flow) return flow;
int used = 0;
vis[x] = 1;
for (int &i = cur[x]; i && used < flow; i = e[i].next) {
int y = e[i].to;
if (dis[y] != dis[x]+e[i].c || vis[y]) continue ;
int tmp = dfs(y, min(flow-used, e[i].w));
if (tmp) {
e[i].w -= tmp, e[i^1].w += tmp;
used += tmp;
totc += tmp*e[i].c;
}
}
vis[x] = 0;
return used;
}
int MCMF(int x, int y) {
int ans = 0; S = x, T = y, totc = 0;
while (spfa()) ans += dfs(S, INF);
return totc;
}
应用
方格取数
例题:洛谷P2045 方格取数加强版
给出一个 \(n\times n\) 的矩阵,每一格有一个非负整数 \(A_{i,j}\) ( \(A_{i,j}\leq 10^3\) ),现在从 \((1,1)\) 出发,可以往右或者往下走,最后到达 \((n,n)\) ,每达到一格,把该格子的数取出来,该格子的数就变成 \(0\) ,这样一共走 \(K\) 次,现在要求 \(K\) 次所达到的方格的数的和最大。
该问题有不少的变体,但总体的核心不变,用同样的思维即可解决。考虑到每个数只能被取一次,我们将点拆成出点与入点,然后连一条入点到出点的容量为 \(1\) ,费用为数字大小。但是注意到即使数字已经被取了,下次仍然能经过,于是有再连一条容量为 \(\infty\) ,费用为 \(0\) 的边,表示不取数字随便走。最后跑一遍最大费用最大流即可。
程序段:
int main() {
n = read(), k = read();
S = 2*n*n+1, cntn = T = S+1;
addE(S, 1, k, 0), addE(2*n*n, T, k, 0);
rep (i, 1, n) rep (j, 1, n) {
int x = read();
addE(getid(i, j), getid(i, j)+n*n, INF, 0);
addE(getid(i, j), getid(i, j)+n*n, 1, -x);
}
rep (i, 1, n) rep (j, 1, n) {
if (i != n)
addE(getid(i, j)+n*n, getid(i+1, j), INF, 0);
if (j != n)
addE(getid(i, j)+n*n, getid(i, j+1), INF, 0);
}
MCMF();
printf("%d", -totc);
return 0;
}
建模思想
网络流的精髓并不在于对算法的简单应用,而是在与图论建模思想相结合来处理许多类型问题,下面会列举一些建模思想。
拆点思想
我们知道,网络流能对边权进行非常好的处理,但是不能处理点相关的限制。这时候我们就可以将点拆成两个点,再在两个点之间连上一条边,通过边的容量进行限制。教辅的组成是这个思想一个非常基础的应用,通过拆点再连上容量为 \(1\) 的边来限制第二类教辅只能被使用一次。
拆点思想在实际解决问题中的使用非常多样,如最小路径覆盖问题中将点拆掉以形成二分图。因此,在解决问题时,可以尝试通过拆点转化出性质优秀的模型。
棋盘染色
棋盘染色就是在矩阵中对所有的点像国际象棋的棋盘那样黑白染色,然后得到黑点与白点是二分图。这样一来,就可以用网络流算法轻松解决了。比较经典的题目有方格取数问题。
参考资料
图片制作:Graph Editor
题目来源:洛谷
部分内容证明参考:网络流/二分图相关笔记(干货篇) - command_block、OI Wiki


