ACM - 最短路 - AcWing 851 spfa求最短路
题解
以此题为例介绍一下图论中的最短路算法 \(Bellman\)-\(Ford\) 算法。算法的步骤和正确性证明参考文章最短路径(Bellman-Ford算法)
松弛函数
对边集合 \(E\) 中任意边，\(w(u,v)\) 表示顶点 \(u\) 到顶点 \(v\) 的边的权值，用 \(d[v]\) 表示当前从起点 \(s\) 出发到顶点 \(v\) 的最短距离。
若存在边 \(e\)，权值为 \(w(u,v)\)，使得：
则更新 \(d[v]\) 值
松弛函数作用：判断经过某个顶点，或者某条边，是否可以缩短起点到终点的当前最短距离（路径权值）。
松弛函数迭代
以对边集合 \(E\) 中每条边执行一次迭代函数作为一次迭代（称为松弛函数迭代），我们可以判断，只需经过有限次迭代，即可确保计算出起点到每个顶点的最短距离。
以下图作为示例示例演示松弛函数迭代过程。
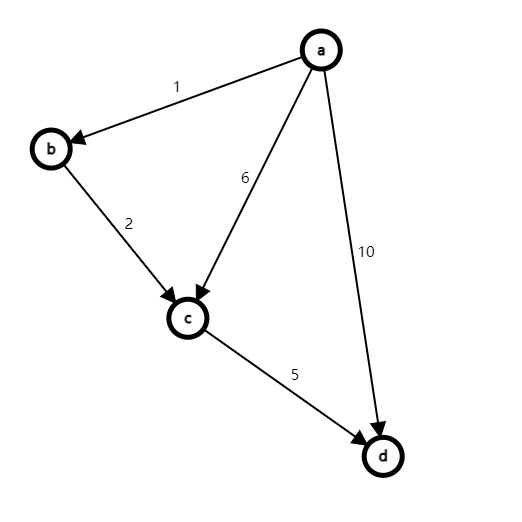
为了凸显出过程的特点，我们直接在最坏情况下分析。
用 \(d[v]\) 表示起点 \(s\) 到顶点 \(v\) 的当前最短距离，以 \(\delta(u,v)\) 表示顶点 \(u\) 到顶点 \(v\) 的全局最短距离，集合 \(S\) 表示当前已找到全局最短距离的顶点集。
迭代前，分别设置为
第一次迭代
- 对边 \(w(c,d)\) 执行松弛函数，则 \(d[d]=\infty\)
- 对边 \(w(b,c)\) 执行松弛函数，则 \(d[c]=\infty\)
- 对边 \(w(a,b)\) 执行松弛函数，则 \(d[b]=d[a]+w(a,b)=1\)
- 对边 \(w(a,c)\) 执行松弛函数，则 \(d[c]=d[a]+w(a,c)=6\)
- 对边 \(w(a,d)\) 执行松弛函数，则 \(d[d]=d[a]+w(a,d)=10\)
第一轮迭代，有三条边起到了松弛效果，直观的可以看出 \(d[b] = \delta(a,b)\)，此时有一个顶点获得了全局最短距离，\(S = \{ a, b \}\)。
第二次迭代
- 对边 \(w(c,d)\) 执行松弛函数，则 \(d[d]=10\)
- 对边 \(w(b,c)\) 执行松弛函数，则 \(d[c]=d[b] + w(b,c)=3\)
- 对边 \(w(a,b)\) 执行松弛函数，则 \(d[b]=1\)
- 对边 \(w(a,c)\) 执行松弛函数，则 \(d[c]=3\)
- 对边 \(w(a,d)\) 执行松弛函数，则 \(d[d]=10\)
第一轮迭代，有三条边起到了松弛效果，直观的可以看出 \(d[c] = \delta(a,c)\)，此时有一个顶点获得了全局最短距离，\(S = \{ a, b, c \}\)。
第三次迭代
- 对边 \(w(c,d)\) 执行松弛函数，则 \(d[d]=d[c] + w(c,d)=8\)
- 对边 \(w(b,c)\) 执行松弛函数，则 \(d[c]=3\)
- 对边 \(w(a,b)\) 执行松弛函数，则 \(d[b]=1\)
- 对边 \(w(a,c)\) 执行松弛函数，则 \(d[c]=3\)
- 对边 \(w(a,d)\) 执行松弛函数，则 \(d[d]=8\)
第一轮迭代，有三条边起到了松弛效果，直观的可以看出 \(d[d] = \delta(a,d)\)，此时有一个顶点获得了全局最短距离，\(S = \{ a, b, c, d \}\)。
迭代次数（算法正确性）
对于顶点 \(v\)，若此时有 \(d[v] = \delta(s, v)\)，即顶点 \(v\) 的全局最短距离已被确定，则称顶点 \(v\) 为已确定顶点。若 \(v \notin S\)，则需要将顶点 \(v\) 加入到集合 \(S\) 中。
有下面定理：
若一个图中存在未确认顶点，则对边集合的一次松弛迭代后，会增加至少一个已确认顶点。具体地说，至少增加的已确认顶点为 \(\arg\min_{j \in V - S} d[j]\)。
定理证明
令
-
\(V\) 为图的顶点集；
-
\(S\) 为已找到全局最短距离的顶点集；
-
\(T=V-S\) 为未找到全局最短距离的顶点集。
初始情形
初始情况下，只有顶点 \(s\) 属于已确定顶点（\(s \in S\)）， 此时有两种情况：起点 \(s\) 不存在相邻顶点；起点 \(s\) 存在相邻顶点。对于第一种情况，此时已找到全局最短距离，算法结束。对于第二种情况，我们证明，在对边集合进行一次松弛迭代后，必定会增加至少一个已确认顶点。
对于第二种情形，初始
第一轮松弛迭代后，令 \(k = \arg\min_{j \in V - S} d[j]\)，则 \(k\) 是起点 \(s\) 的相邻顶点（所有非相邻顶点在第一轮迭代后当前最短距离都仍为 \(\infty\)）。此时 \(d[k] = w(s,k)\)，我们说 \(k\) 此时达到了全局最短距离，否则若 \(d[k]\) 没有达到全局最短距离，存在一条路径更短（下式），其中 \(r\) 为相邻顶点。
相比较而言，当前最短距离 \(d[k]\) 对应的路径为
- 若 \(r = k\)，则 \(p’ = \langle s, k, \cdots, k \rangle\)，路径 \(p'\) 的权值小于路径 \(p\) 的权值，说明路径 \(\langle k, \cdots, k \rangle\) 权值为负，即图中存在负权回路，矛盾。如下图所示
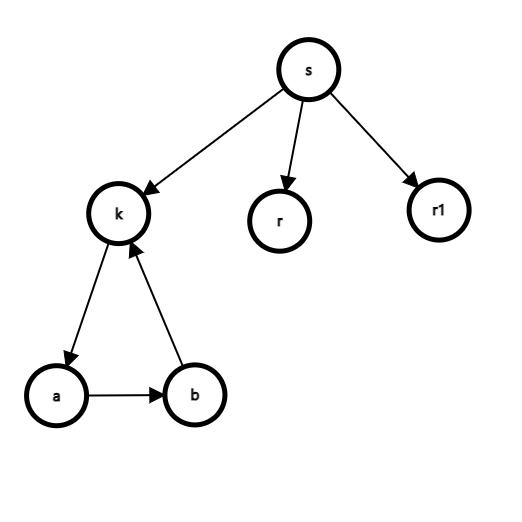
- 若 \(r \neq k\)，对于路径 \(p’\) 中的 \(\langle s, r \rangle\) 部分，由于对于任意相邻顶点 \(v\)，存在 \(d[k] \leqslant d[v]\)，所以有 \(d[k] \leqslant d[r]\)，导出矛盾。
一般情形
已确认顶点集合为 \(S\)，进行一次松弛迭代后，令 \(k = \arg\min_{j \in V - S} d[j]\)，则 \(k\) 是集合 \(S\) 中某个点的相邻顶点（所有非相邻顶点此时当前最短距离都仍为 \(\infty\)，更详细的证明用归纳法）。
我们说 \(k\) 此时达到了全局最短距离，否则若 \(d[k]\) 没有达到全局最短距离，存在一条路径更短（下式），其中 \(t \in T\) 。
相比较而言，当前最短距离 \(d[k]\) 对应的路径为下式，其中 \(r \in S\)，\(p_1\) 为 \(S\) 到 \(r\) 的最短路径，归纳法易知 \(p_1\) 路径经过的所有点 \(v\)，有 \(v \in S\)。
对于 \(t\)，有两种情况：\(t\) 是集合 \(S\) 中某个点的相邻顶点，由于 \(d[t] \leqslant d[k]\)，故 \(p'\) 的路径权值必定比 \(p\) 的路径权值要大，矛盾；\(t\) 不是集合 \(S\) 中某个点的相邻顶点，此时 \(d[t] = \infty\)，矛盾。
故当前最短距离 \(d[k]\) 达到了全局最短距离。
证毕。
程序设计
为方便展示，用 Python 代码实现松弛函数：
# distance 列表存储从起点到当前顶点的路径权值
# parent 列表存储到当前顶点的前驱顶点下标值。
# 初始 distance 列表和parent 列表元素皆为 None，表示路径权值无穷大
def releax(edge, distance, parent):
if distance[edge.begin - 1] == None:
pass
elif distance[edge.end - 1] == None or distance[edge.end - 1] > distance[edge.begin - 1] + edge.weight:
distance[edge.end - 1] = distance[edge.begin - 1] + edge.weight
parent[edge.end - 1] = edge.begin - 1
return True
return False
利用松弛函数实现 \(Bellman-Ford\) 算法。
# times 变量用于记录迭代的执行次数
# edges 列表是存储边的集合
# getEdgesFromAdjacencyList 函数用于从邻接矩阵中转换出边的集合
def bellman_ford(graph, start, end):
distance, parent = [None for i in range(graph.number)], [None for i in range(graph.number)]
times, distance[start - 1], edges = 1, 0, getEdgesFromAdjacencyList(graph)
while times < graph.number:
for i in range(len(edges)):
releax(edges[i], distance, parent)
times += 1
for i in range(len(edges)):
if releax(edges[i], distance, parent):
return False
return True
算法优化
对于 \(Bellman-Ford\) 算法的一种常见实现是使用队列优化。在中国的 IO 届也常称该算法为 \(SPFA\) 算法。
在 \(Bellman-Ford\) 算法介绍过程中我们会发现，有些边的松弛操作没有必要，我们可以证明如下结论：
一条边执行了松弛操作，当且仅当这条边的起点的当前最短距离之前被更新了。
在迭代过程中，每次取出队列的首节点，遍历该节点的所有出边，判断每条出边是否执行了松弛操作，若该边执行了松弛，则说明边对应的终点的当前最短距离 \(dist\) 被更新了，就将该点压入到队列 \(queue\) 中。
若存在负权回路，则该迭代过程会是一个死循环，但我们可以通过负权回路的特点来判断负权回路从而终止循环。负权回路的判断见另一篇文章。
算法正确性证明
在一轮取节点——遍历出边结束后，我们会发现此时图的所有边只有两种：
-
松弛一定无效的边
-
松弛可能有效的边
当前队列若为：
对图中任意一条边，它一定有起点和终点，起点若在队列内，说明该边为松弛可能有效的边；起点若不在队列内，说明该边为松弛一定无效的边。
因此，当退出循环时，退出的判定条件为队列为空，说明了此时所有边都一定是松弛一定无效的边，这是我们说所有点的 \(dist\) 都达到的最短路径。否则存在至少一点没有达到最短路径，即对于该点存在一条更短的路径，而更短路径的存在说明松弛可能有效的边也一定存在，矛盾。
符号说明一下，设原路径为
更短路径为
则此时必有
即说明了松弛有效的边的存在性。
我们还需证明当无负权回路时，循环一定终止。反证法，若循环为死循环，则我们断言存在一点 \(c \in V\)，它在队列 \(queue\) 中出现了无穷多次，则 \(c\) 被松弛了无穷多次。由于以 \(c\) 为终点的边只有有限条，而松弛了 \(c\) 点的边有无限条，因此负权回路必定存在，矛盾，循环的终止性成立。
综上，\(SPFA\) 算法正确。
队列优化算法的程序设计
实现代码如下：
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<vector>
#include<queue>
#define PII pair<int, int>
#define INF 0x3f3f3f3f
using namespace std;
const int N = 100010;
int n, m, q;
vector<PII> E[N]; // 用邻接表存储边
int dist[N]; // 第i号点距离源点的当前最短距离
bool vis[N]; // vis数组存的是当前结点是否在队列中
int spfa()
{
// 初始化
memset(dist, 0x3f, sizeof(dist));
dist[1] = 0;
queue<int> q;
q.push(1);
vis[1] = true;
// 队列优化的 Bellman-Ford 算法
while (!q.empty()) {
// 弹出队列首节点
int t = q.front();
q.pop();
// 首节点弹出，vis更新
vis[t] = false;
// 遍历首节点的所有出边
for (int i = 0, len = E[t].size(); i < len; ++i) {
int j = E[t][i].first, k = E[t][i].second;
if (dist[j] > dist[t] + k) {
dist[j] = dist[t] + k;
if (!vis[j]) {
vis[j] = true;
q.push(j);
}
}
}
}
return dist[n];
}
int main()
{
cin >> n >> m;
int u, v, w;
for (int i = 0; i < m; ++i) {
cin >> u >> v >> w;
E[u].push_back({ v, w });
}
int tmp = spfa();
if (tmp >= INF) cout << "impossible" << endl;
else cout << tmp << endl;
return 0;
}
最短路算法对比
| 算法 | \(Floyd\) | \(Dijkstra\) | \(Bellman\)-\(Ford\) |
|---|---|---|---|
| 空间复杂度 | \(O\)\((V^2)\) | \(O\)\((E)\) | \(O\)\((E)\) |
| 时间复杂度 | \(O\)\((V^3)\) | 看具体实现 | \(O\)\((VE)\) |
| 负权边时是否可以处理 | 可以 | 不能 | 可以 |
| 判断是否存在负权回路 | 不能 | 不能 | 可以 |
其中 \(V\) 表示图的顶点数，\(E\) 表示图的边数。
