ACM - 最短路 - CodeForces 295B Greg and Graph
CodeForces 295B Greg and Graph
题解
\(Floyd\) 算法是一种基于动态规划的算法，以此题为例介绍最短路算法中的 \(Floyd\) 算法。
我们考虑给定一个图，要找出 \(i\) 号点到 \(j\) 号点的最短路径。则该最短路径只有两种可能：
-
\(i\) 号点直接到达 \(j\) 号点的路径中产生最短路径
-
\(i\) 号点经过一些中间点到达 \(j\) 号点的路径中产生最短路径
我们添加一个点 \(k\)，使得 \(i\) 号点到 \(j\) 号点再添加后产生的最短路径比添加前的最短路径更短，则称该操作为松弛。
下面我们以从一个示例开始介绍算法的步骤。
示例
给定一个赋权有向图，如下图：
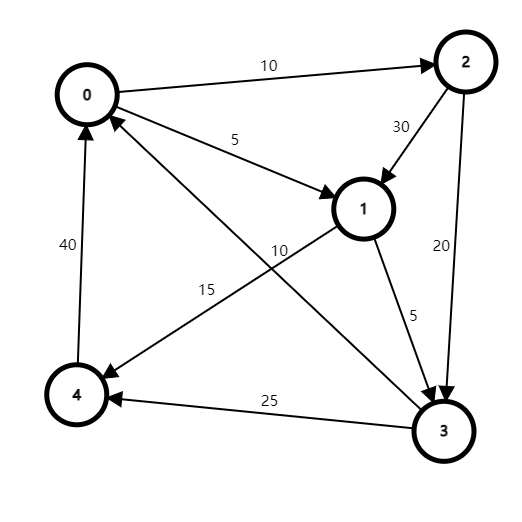
我们声明一个集合 \(S\)，并称该集合为中转集合。
我们声明一个 \(dist\) 数组，其中 \(dist[i][j]\) 表示从源点 \(i\) 号点只经过中转集合中的点，到达目标点 \(j\) 号点的最短路径。
每一轮更新都更新 \(dist\)，直到集合 \(S\) 为图的顶点集 \(V\)。
初始化更新
\(S\) 初始化为：
\(dist\) 数组根据我们的定义，此时 \(dist[i][j]\) 表示不经过图中的任何顶点，直接从源点 \(i\) 号点到达 \(j\) 号点的最短距离，为了方便书写，我们此处采用图的邻接矩阵表示。
故 \(dist\) 被初始化为：
第一轮更新
\(S\) 更新为：
\(dist\) 数组根据我们的定义，此时 \(dist[i][j]\) 表示由图中 \(0\) 号点中转，直接从源点 \(i\) 号点到达 \(j\) 号点的最短距离。该最短路径有两种可能：
- 最短路径经过 \(0\) 号点；
- 最短路径不经过 \(0\) 号点；
对于第 \(1\) 种情况说明 \(0\) 号点可以松弛之前的最短距离。这两种情况可以统一表示为下式：
此处我们应该注意一下更新的顺序问题，上式表达的含义应该是指只由上一轮的 \(dp[i][j]\)、\(dp[i][0]\) 和 \(dp[0][j]\) 来更新出这一轮的 \(dp[i][j]\)。更准确地说应该可以扩展下数组 \(dist\) 的维度。 如下图所示：
其中 \(k\) 表示这是第 \(k\) 轮更新。按我们的意思，应该写成：
即只由第 \(0\) 轮的 \(dp[i][j]\)、\(dp[i][0]\) 和 \(dp[0][j]\) 来更新出第 \(1\) 轮的 \(dp[i][j]\)。那我们为什么可以写成式 \(1\) 的样子？原因在于 \(dp[i][0]\) 和 \(dp[0][j]\) 在此轮更新循环中，始终都没有被更新。后面会更详细地说明这个问题。
故 \(dist\) 被更新为：
第二轮更新
\(S\) 更新为：
\(dist\) 数组根据我们的定义，此时 \(dist[i][j]\) 表示从源点 \(i\) 号点出发，只经过中转集合 \(S\) 中的点，到达 \(j\) 号点的最短距离。该最短路径有两种可能：
- 最短路径经过 \(1\) 号点；
- 最短路径不经过 \(1\) 号点；
对于第 \(1\) 种情况说明 \(1\) 号点可以松弛之前的最短距离。这两种情况可以统一表示为下式：
我们接着就要问了，为什么经过 \(1\) 号点的最短路径距离等于 \(dist[i][1] + dist[1][j]\)。在第一轮更新的时候容易想到，但这轮更新（第二轮更新）中，该问题需要仔细思考一下。
经过 \(1\) 号点的路径这样表示：\(i\)(源点) \(\to\) \(1\) \(\to\) \(j\)(目标点)。而经过 \(1\) 号点的最短路径一定是由 \(i\) 到 \(1\) 的最短路径和 \(1\) 到 \(j\) 的最短路径构成（反证法即可得）。
我们应用这个性质，重新表述为：经过 \(1\) 号点的从源点 \(i\) 出发，由 \(S - \{1\}\) 集合中转到达目标点 \(j\) 的最短路径一定是由从源点 \(i\) 出发，由 \(S - \{1\}\) 集合中转到达目标点 \(1\) 的最短路径和从源点 \(1\) 出发，由 \(S - \{1\}\) 集合中转到达目标点 \(j\) 的最短路径构成（正确性显然，只是由原来的范围全路径集合缩小为\(S - \{1\}\) 集合中转的那些路径构成的集合）。
而此轮更新仍然不会改变 \(dist[i][1]\) 和 \(dist[1][j]\) 的值，因此不用关心更新顺序的问题。
综上，上式完全正确。故 \(dist\) 应该被更新为：
第三轮更新
\(S\) 更新为：
状态转移方程为：
状态转移方程的正确性证明完全同上，而由归纳法容易知道对之后的更新该状态转移方程仍然正确。而该轮仍然不会改变 \(dist[i][2]\) 和 \(dist[2][j]\) 的值，因此不用关心更新顺序的问题。
故 \(dist\) 应该被更新为：
第四轮更新
\(S\) 被更新为：
\(dist\) 被更新为：
第五轮更新
\(S\) 被更新为：
\(dist\) 被更新为：
此时 \(S\) 集合等于图的顶点集 \(V\)。停止迭代。
最后得到的 \(dist[i][j]\) 就表示源点 \(i\) 到达目标点 \(j\) 的最短路径距离。
程序设计
为了能清晰严谨的说明，我们可以将 \(dist[i][j]\) 设成 \(dist[i][j][k]\)。每次循环用 \(dist[i][j][k - 1]\) 来更新 \(dist[x][y][k]\)（即用上一层的 \(dist\) 来更新这一层的 \(dist\)）。但实际上，我们发现可以通过减少一个维度来减小空间复杂度，虽然这时我们要注意更新顺序的问题，但可以进一步发现每次迭代 \(dist[i][m]\) 和 \(dist[m][j]\) 都没有发生被更新为新值，即对应的 \(dist\) 的第 \(m\) 行和第 \(m\) 列都没有发生变化，这可以使得更新顺序可以任意。
如下图展示了在某一次迭代中更新 \(dist[3][4]\) 的过程，对应的公式描述为：
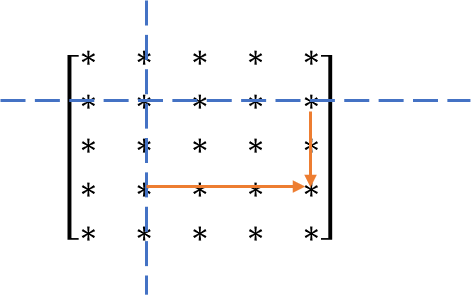
上图表示那次迭代过程中，第 \(1\) 行和第 \(1\) 列的值都没有被更新为新值，正是由此，明显可以看出 \(dist[i][j]\) 的更新顺序确实可以任意。
程序的主要部分可以写出来：
// n : 表示图的顶点数
for (int k = 0; k < n; ++k) {
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
最短路算法对比
| 算法 | \(Floyd\) | \(Dijkstra\) | \(Bellman\)-\(Ford\) |
|---|---|---|---|
| 空间复杂度 | \(O\)\((V^2)\) | \(O\)\((E)\) | \(O\)\((E)\) |
| 时间复杂度 | \(O\)\((V^3)\) | 看具体实现 | \(O\)\((VE)\) |
| 负权边时是否可以处理 | 可以 | 不能 | 可以 |
| 判断是否存在负权回路 | 不能 | 不能 | 可以 |
其中 \(V\) 表示图的顶点数，\(E\) 表示图的边数。
运用 \(Floyd\) 算法解决该题
题目大意：每次删去一个点，求当前删去该点之前，所有点对最短路径之和。
在每删除一个点前，题目明显要求求出的最短路径不是单源，而是多源的。具体地说，第一，针对所有当前存在的点对；第二，对每一对点对求最短路径。
每次删去一个点，直到把所有点都删尽。倒过来就相当于每次加入一个点，而恰好 \(Floyd\) 算法的建立过程中 \(dist\) 数组便记录了这些信息，所以逆序使用 \(Floyd\) 算法即可。
程序：
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
typedef pair<int, int> PII;
#define LL long long
int n, m;
int graph[505][505]; // 邻接矩阵存图
int del[505]; // 删除点的序号
LL sum[505]; // 删除点对前，点对的最短距离和
int dist[505][505];
int main()
{
// 输入图的邻接矩阵
cin >> n;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
cin >> m;
graph[i][j] = m;
}
}
// 输入图的顶点删除顺序
for (int i = 1; i <= n; ++i) cin >> del[i];
// 初始化 dist 数组
memset(dist, 0x3f, sizeof(dist));
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
dist[i][j] = graph[i][j];
}
}
// 根据删除的点的序号，我们逆向添加点，运行Floyd算法
int add[505];
memset(add, 0, sizeof(add));
for (int k = n; k >= 1; --k) {
add[del[k]] = 1;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
dist[i][j] = min(dist[i][j], dist[i][del[k]] + dist[del[k]][j]);
}
}
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
if (add[i] && add[j]) sum[k] += dist[i][j];
}
}
}
for (int k = 1; k <= n; ++k) printf("%I64d ", sum[k]);
printf("\n");
return 0;
}
