ACM - 最短路 - AcWing 849 Dijkstra求最短路 I

AcWing 849 Dijkstra求最短路 I

题解

以此题为例介绍一下图论中的最短路算法。先让我们考虑以下问题：

给定一个 $n$ 个点 $m$ 条边的有向图（无向图），图中可能存在重边和自环，给定所有边的边权。请求出给定的一点到另一点的权值之和最小的一条路径。

上述问题即所谓的最短路问题。解决这类问题的常用最短路算法：

• $Floyd$ 算法（多源最短路径）

• $Dijkstra$ 算法（没有负权边的单源最短路径）

• $Bellman$-$Ford$ 算法（含有负权边的单源最短路径）

另外还有著名的启发式搜索算法 —— $A*$ 算法。我们以此题为模板来学习 $Dijkstra$ 算法。

示例

给定一个图来演示算法过程，以下图为例求解从 $0$ 号点（称为源点）出发到其余点的最短路径的距离。

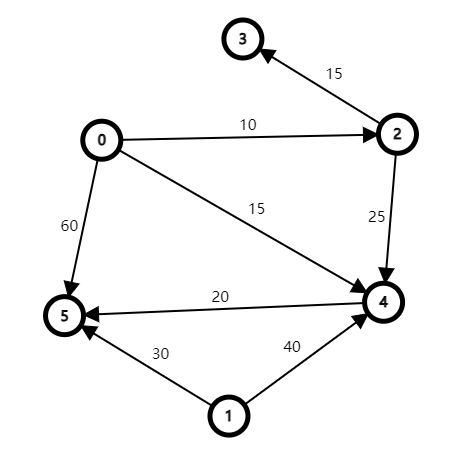
初始化更新

声明一个 $S$ 数组（取 $short$ 首字母）,用来记录当前更新中已找到全局最短距离的点的编号。

声明一个 $dist$ 数组，用来记录源点只能先到达集合 $S$ 中的点，再直接到达目标点的那些路径（即中间没有经过 $S$ 以外的点就直接到目标点）的最短距离（源点 $\to$ $S$ $\to$ 目标点）。

在初始化更新中，$S$ 数组更新为：

$$S = [0]$$

$dist$ 数组被更新为：

$$dist = [0, \infty, 10, \infty, 15, 60]$$

解释上述更新。

初始的 $S$ 数组为 $[0]$（源点编号）。

$dist[0]$ 表示 $0$ 号点（源点）先到 $S$ 数组中的点，再到 $0$ 号点（目标点）的最短距离，即使可能存在自环，由于 $Dijkstra$ 算法的使用前提是非负权（即边的权值大于等于 $0$），因此源点到自己的最短距离肯定为 $0$。

$dist[1]$ 表示 $0$ 号点（源点）先到 $S$ 数组中的点，再到 $1$ 号点（目标点）的最短距离，由于此时 $S$ 数组中只有一个 $0$ 号点（源点），而 $0$ 号点到 $1$ 号点没有边直接连接，因此为 $\infty$（表示不能先到 $S$ 数组中的点，再到达 $1$ 号点）。

其余点可类似解释。

第一轮更新

更新 $S$ 数组

设 $V = [0, 1, 2, 3, 4, 5]$（图的所有点）。

在第一轮更新中，我们取 $V - S$ 中 对应 $dist$ 数组数值最小的那个点，即 $2$ 号点（$10$ 小于 $15$、$60$、$\infty$），此时 $S$ 数组更新为：

$$S = [0, 2]$$

根据我们对 $S$ 数组的解释，此时 $2$ 号点的 $dist[2]$ 已到达全局最短距离，此时我们不禁会想，这就达到最短距离了？难道 $dist[2] = 10$ 就是 $0$ 号点（源点）到 $2$ 号点的最短距离了？

令 $T = V - S = [1, 3, 4, 5]$，则源点到 $2$ 号点的最短路径只能为以下两种情况（中间点全为 $S$ 中的点，中间点有一个不为 $S$ 中的点）：

1. 源点 $\to$ $S$ $\to$ $2$ 号点 （$S=[0]$，为了方便说明此处把目标点剔除）
2. 源点 $\to$ $t \in T$ $\to$ $2$ 号点 （$T=[1, 3, 4, 5]$）

注：源点直接到 $2$ 号点的情况包含在第一种情况（因 $S$ 始终含源点）。

显然最短路径不会是第二种情况（这是算法正确性证明的核心，在之后几轮更新里该性质并不明显）。

更新 $dist$ 数组

然后重新更新 $dist$ 数组（因 $S$ 数组被扩充了，而 $dist$ 依赖 $S$），$dist$ 数组更新为：

$$dist = [0, \infty, 10, 25, 15, 60]$$

可以看到只有一个值被更新了。记扩充前的 $S$ 为 $S1$（此时 $S1 = [0]$），由 $dist$ 数组的含义，我们只需比较得出是否新加入的点使得当前最短路径更短。

$$dist[i] = \min \left( dist[i], dist[2] + graph[2][i] \right)$$

注意，上述等号理解为赋值。此处为书写方便，使用图的邻接矩阵表示 $graph$。

比如更新 $dist[3]$。更新前 $dist[3]$ 表示从源点出发，先到 $S1$ 中的点，再到目标点（$3$ 号点）的最短路径距离；更新后 $dist[3]$ 应该为从源点出发，先到 $S1 + [2]$ 中的点，再到目标点（$3$ 号点）的最短路径距离。

我们重新明确一下更新后的最短路径可能的情况（注意，此处非常关键），对于该最短路径，我们考虑目标点（$3$ 号点）的上一个点（！！！！！），该点只能为此轮扩充点（$2$ 号点），或者不是此轮扩充点（非 $2$ 号点），如果是扩充点，则该最短路径距离为 $dist[2] + graph[2][i]$；如果不是扩充点，则该最短路径为 $dist[i]$。

嗯？上个点不是扩充点的情况为 $dist[i]$？想想也确实，上个点在 $S$ 中，但不是扩充点，说明必为 $S1$ 中的点，而 $S1$ 中的点在上一轮更新中已经保证全局最短距离。为更清晰地展示，我们列出更新后最短路径的可能情况：

1. 源点 $\to$ 非扩充点 $\to$ 目标点上个点（非扩充点） $\to$ 目标点
2. 源点 $\to$ 非扩充点 $\to$ 目标点上个点（扩充点） $\to$ 目标点
3. 源点 $\to$ 扩充点 $\to$ 目标点上个点（非扩充点） $\to$ 目标点
4. 源点 $\to$ 扩充点 $\to$ 目标点上个点（扩充点） $\to$ 目标点

目标点上个点有两种可能：扩充点和非扩充点；源点到目标点上个点的路径有两种可能：经过扩充点和不经过扩充点。易知，第 $3$ 种和第 $4$ 种情况都一定不是最短路径（第 $3$ 种情况非最短是由于目标点上个点在 $S1$ 中）。因此只更新第 $1$ 种和第 $2$ 种情况产生的最短路径即可。

第二轮更新

更新 $S$ 数组

根据上面的规则，我们选取此轮的扩充点为 $4$ 号点（$dist[4]$ 在非 $S$ 点中最小，$15$ 小于 $25$、$60$、$\infty$），因此 $S$ 数组被更新为：

$$S = [0, 2, 4]$$

根据我们对 $S$ 数组的解释，此时 $4$ 号点的 $dist[4]$ 已到达全局最短距离。

此时 $T = V - S = [1, 3, 5]$，源点到 $4$ 号点的最短路径只能为以下两种情况：

1. 源点 $\to$ $S$ $\to$ $4$ 号点 （$S=[0, 2]$，为了方便说明此处把目标点剔除）
2. 源点 $\to$ $t \in T$ $\to$ $4$ 号点 （$T=[1, 3, 5]$）

我们说，此时最短路径不可能为第 $2$ 种情况，正是这性质使得源点到 $4$ 号点的最短路径只能为第 $1$ 种情况，即 $dist[4]$ 为全局最短距离。

由于 $S$ 数组包含源点，因此第 $2$ 种情况也可以写成 源点 $\to$ $S$ $\to$ $t \in T$ $\to$ $4$ 号点。此时写成：

1. （源点 $\to$ $S$ $\to$ $4$ 号点）
2. （源点 $\to$ $S$ $\to$ $t_1 \in T$） $\to$ $4$ 号点（此处 $t_1$ 为路径中出现的第一个 $T$ 中的点）

由于 $dist[t] \geqslant dist[4]$，显然第 $1$ 种情况产生最短路径。

更新 $dist$ 数组

此时的扩充点为 $4$ 号点，由 $dist$ 数组的含义，我们只需比较得出是否新加入的点使得当前最短路径更短。由式子：

$$dist[i] = \min \left( dist[i], dist[4] + graph[4][i] \right)$$

更新 $dist$ 数组得：

$$dist = [0, \min(\infty,\infty), 10, \min(25, 15 + \infty), 15, \min \left( 60, 15 + 20 \right)] = [0, \infty, 10, 25, 15, 35]$$

第三轮更新

此轮加入的扩充点为 $3$，$S$ 数组更新为：

$$S = [0, 2, 4, 3]$$

根据加入的扩充点更新数组 $dist$ 为：

$$dist = [0, \min(\infty,\infty), 10, 25, 15, \min \left( 35, 25 + \infty \right)] = [0, \infty, 10, 25, 15, 35]$$

第四、五轮更新

加入的扩充点按顺序为 $5$、$1$。$S$ 数组更新为：

$$S = [0, 2, 4, 3, 5, 1]$$

数组 $dist$ 被更新为与原来一致，即：

$$dist = [0, \infty, 10, 25, 15, 35]$$

算法步骤

下面给出算法：

输入：赋权有向图 $G(V, E, W)$。
输出：源点 $v_0$ 到其余各点的最短距离。

1. 初始化 $S = \{ v_0 \}$，遍历所有点，初始化当前最短距离 $dist[i] = graph[v_0][i]$

2. $S$ 不等于 $V$，执行循环 $2-5$，若等于，转 $6$

3. 确定扩充点 $m = \arg\min_{j \in V - S} dist[j]$

4. 加入扩充点 $m$，$S = S + \{ m \}$

5. 更新 $dist$。遍历 $V - S$ 所有点，$dist[i] = \min \left( dist[i], dist[m] + graph[m][i] \right)$

6. 结束。

从给出的算法步骤可以看出，整个算法大部分时间都在执行两层循环。外层循环是从第 $2$ 步执行到 第 $5$ 步，由于每一次循环我们都给 $S$ 数组增加一个扩充点，外层循环执行次数为顶点数；而内层循环的时间复杂度则较为复杂，其复杂的原因也是 $Dijkstra$ 算法拥有良好扩展性的原因：使用何种数据结构实现算法。

一般来说，其具体实现方式有四种：

• 顺序遍历集合 $V - S$ 确定扩充点
• 使用二叉堆作为优先队列确定扩充点
• 使用二项堆作为优先队列确定扩充点
• 使用斐波那契堆堆作为优先队列确定扩充点

我们有二叉堆、二项堆和斐波那契堆的各个操作的时间复杂度（来自《算法导论》）：

设图中的顶点数为 $V$，边数为 $E$，则平均每个点的边数为 $k = E/V$。对于 $Dijkstra$ 算法，我们可以得到统一的时间复杂度计算公式：

$$(V - 1) \times (T_{EXTRACT-MIN} + T_{DELETE} + T_{DECREASE-KEY} \times k)$$

对于上述四种具体实现方式，分别计算其时间复杂度：

1. 顺序遍历

$$\begin{align*} & (V - 1) \times (T_{EXTRACT-MIN} + T_{DELETE} + T_{DECREASE-KEY} \times k) \\ & = (V - 1) \times (V + 1 + k) \\ & = V^2 + E \end{align*}$$

2. 二叉堆

$$\begin{align*} & (V - 1) \times (T_{EXTRACT-MIN} + T_{DELETE} + T_{DECREASE-KEY} \times k) \\ & = (V - 1) \times (\lg V + \lg V + k \lg V) \\ & = V \times (2 + k) \times \lg V \\ & = (2 V + E) \lg V \\ & = (V + E) \lg V \\ \end{align*}$$

3. 二项堆

$$\begin{align*} & (V - 1) \times (T_{EXTRACT-MIN} + T_{DELETE} + T_{DECREASE-KEY} \times k) \\ & = (V - 1) \times (\lg V + \lg V + k \lg V) \\ & = V \times (2 + k) \times \lg V \\ & = (V + E) \lg V \\ \end{align*}$$

4. 斐波那契堆堆

$$\begin{align*} & (V - 1) \times (T_{EXTRACT-MIN} + T_{DELETE} + T_{DECREASE-KEY} \times k) \\ & = (V - 1) \times (\lg V + \lg V + k) \\ & = V \times (2 \lg V + k) \\ & = 2 V \lg V + E \\ & = V \lg V + E \\ \end{align*}$$

注，上述等式中的相等均是在“时间复杂度”意义下的相等。

程序设计

我们实现第一种用顺序遍历实现的 $Dijkstra$ 算法。

程序：

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<vector>
using namespace std;

int n, m;

int graph[505][505];  // 邻接矩阵存图
int dis[505];  // dis[i]: 源点先到S集合，再到目标点的最短距离
int vis[505];  // vis[i]：表示i号结点的全局最短距离是否已经找到（0-1数组实现S集合）

int dijkstra()
{
    // 初始化更新
    vis[1] = 1;  // 等价于将源点加入S集合
    dis[1] = 0;  // 源点到自己的最短距离为0
    for (int i = 2; i <= n; ++i) dis[i] = graph[1][i];

    // 开始循环更新（当n号点的最短距离找到时，直接退出循环）
    for (int k = 0; k < n; ++k) {
        // 确定此轮扩充点
        int mi = -1; // mi : min_index，扩充点
        for (int i = 1; i <= n; ++i) {
            if (vis[i] == 0 && (mi == -1 || dis[i] < dis[mi])) mi = i;
        }
        // S集合加入扩充点
        vis[mi] = 1;
        // 更新距离
        for (int i = 1; i <= n; ++i) {
            if (vis[i] == 0) dis[i] = min(dis[i], dis[mi] + graph[mi][i]);
        }
    }

    // 如果起点到达不了n号节点，则返回-1
    if (dis[n] == 0x3f3f3f3f) return -1;
    // 返回起点距离n号节点的最短距离
    return dis[n];
}

int main()
{
    // 初始化
    int x, y, z;
    cin >> n >> m;  // 图有n个顶点，m条边
    memset(graph, 0x3f, sizeof(graph));
    memset(dis, 0x3f, sizeof(dis));
    memset(vis, 0, sizeof(vis));
    for (int i = 0; i < m; ++i) {
        cin >> x >> y >> z;
        if (graph[x][y] > z) graph[x][y] = z; // 处理重边的情况
    }
    // 输出图最短距离
    cout << dijkstra() << endl;
    return 0;
}

我们实现用堆优化的 $Dijkstra$ 算法，也即使用优先队列维护 $V - S$ 中的最小值。

程序：

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
typedef pair<int, int> PII;

int n, m;

vector<vector<pair<int, int> > > graph;  // 邻接表存图
int dis[505];  // dis[i]: 源点先到S集合，再到目标点的最短距离
int vis[505];  // vis[i]：表示i号结点的全局最短距离是否已经找到（0-1数组实现S集合）

int dijkstra() 
{
    dis[1] = 0;
    // 建立优先队列维护最小值
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({ 0, 1 });      // first存储距离，second存储节点编号

    while (heap.size()) {
        // 取出优先队列队首元素（即本轮扩充点）
        PII mi = heap.top();  
        heap.pop();
        int dist = mi.first; int node = mi.second;

        // heap存储的second为节点编号，在执行过程中会出现重复
        // 比如heap中有{2, 3}，表示源点经过S到3号顶点的最短距离为2
        // 下面的for循环会将{2, 3}更新为{1, 3}，但实际执行时没有“修改”，而是优先队列的“压入”(push)
        // “修改” = “压入新值” + “弹出旧值”（第一步“压入”被下面完成，第二步“弹出”被上面执行）
        // {1, 3}在下面被压入heap，{2, 3}在上面被弹出
        if (vis[node]) continue; 
        // 这保证了每轮更新至少出现一个扩充点，因此下面的for执行n-1次（与计算出的时间复杂度吻合）
        vis[node] = 1; 

        for (auto tmp : graph[node]) {  // 取出本轮扩充点的每条出边
            // 事实上只有扩充点的出边对应的点的dis出现变化，其余点的dis未发生变化
            // 这变化使得我们需要更新dis数组和优先队列heap
            int tmpnode = tmp.first;
            int tmpdist = tmp.second;
            if (dis[tmpnode] > dis[node] + tmpdist) { // 松弛
                dis[tmpnode] = dis[node] + tmpdist;
                heap.push({ dis[tmpnode], tmpnode });  // 注意这是“压入”更短的距离，不是“修改”
            }
        }
    }
    if (dis[n] == 0x3f3f3f3f) return -1;
    return dis[n];
}

int main()
{
    // 初始化
    int x, y, z;
    cin >> n >> m;  // 图有n个顶点，m条边
    graph.resize(n + 1);
    memset(dis, 0x3f, sizeof(dis));
    memset(vis, 0, sizeof(vis));
    for (int i = 0; i < m; ++i) {
        cin >> x >> y >> z;
        graph[x].push_back({ y, z });
    }
    // 输出图最短距离
    cout << dijkstra() << endl;
    return 0;
}

最短路算法对比

算法	$Floyd$	$Dijkstra$	$Bellman$-$Ford$
空间复杂度	$O$$(V^2)$	$O$$(E)$	$O$$(E)$
时间复杂度	$O$$(V^3)$	看具体实现	$O$$(VE)$
负权边时是否可以处理	可以	不能	可以
判断是否存在负权回路	不能	不能	可以

其中 $V$ 表示图的顶点数，$E$ 表示图的边数。