ACM - 动态规划 - P1282 多米诺骨牌

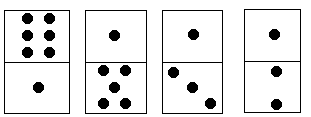
多米诺骨牌由上下 $2$ 个方块组成，每个方块中有 $1 \sim 6$ 个点。现有排成行的上方块中点数之和记为 $S_1$，下方块中点数之和记为 $S_2$，它们的差为 $\left| S_1 - S_2 \right|$。如图，

$$S_1 = 6 + 1 + 1 + 1 = 9, S_2 = 1 + 5 + 3 + 2 = 11, \left| S_1 - S_2 \right| = 2$$

每个多米诺骨牌可以旋转 $180°$，使得上下两个方块互换位置。请你计算最少旋转多少次才能使多米诺骨牌上下 $2$ 行点数之差达到最小。对于图中的例子，只要将最后一个多米诺骨牌旋转 $180°$，即可使上下 $2$ 行点数之差为 $0$。

输入格式

输入文件的第一行是一个正整数 $n (1\leq n\leq 1000)$，表示多米诺骨牌数。接下来的 $n$ 行表示 $n$ 个多米诺骨牌的点数。每行有两个用空格隔开的正整数，表示多米诺骨牌上下方块中的点数 $a$ 和 $b$，且 $1\leq a,b\leq 6$。

输出格式

输出文件仅一行，包含一个整数。表示求得的最小旋转次数。

输入输出样例

输入：

4
6 1
1 5
1 3
1 2

输出：

1

题解

可以考虑用动态规划。该问题要求解的状态为，多米诺骨牌上下两行点数之差最小同时旋转次数最少。

使用二维 $dp$ 数组记录上下点数之差和旋转次数。由于对一堆骨牌的旋转操作不会改变这堆骨牌的点数之和，如果记录了上点数，下点数就为总点数 $-$ 上点数（总点数在输入时预处理即可得到）。此时我们可以具体地说，$dp[i][j]$ 表示前 $i$ 个骨牌，上一行点数之和为 $j$ 时的最小旋转次数。

状态转移方程

$dp[i][j]$ 表示前 $i$ 个骨牌，上一行点数之和为 $j$ 时的最小旋转次数。

对于第 $i$ 个骨牌，它可以选择“旋转”或是“不旋转”。如果“不旋转”，则此时的最小旋转次数需由 $dp[i - 1][j - a[i]]$确定，即前 $i - 1$ 个骨牌，上一行点数之和为 $j - a[i]$ 时的最小旋转次数决定；如果“旋转”，则此时的最小旋转次数需由 $dp[i - 1][j - b[i]]$确定，即前 $i - 1$ 个骨牌，上一行点数之和为 $j - b[i]$ 时的最小旋转次数决定。

可以写出如下状态转移方程：

$$dp[i][j] = \min (dp[i - 1][j - a[i]]， dp[i - 1][j - b[i]] + 1)$$

状态搜索方向

初始化二维 $dp$ 数组的第一行，然后递增行数，对每一行从左至右搜索。

初始值所有的 $dp[i][j]$ 为 $\inf$，$dp[1][b[1]] = 1$，$dp[1][a[1]] = 0$（注意初始化顺序不能交换，想想为什么？？）。

考虑我们的状态搜索方向，在更新 $dp[i][j]$ 的值时，$i - 1$是完全正确的，但 $j$、$a[i]$、$b[i]$会出现三种情况。

1. $j$ 大于等于这两者；
2. $j$ 只大于等于其中一个，而小于另一个；
3. $j$ 小于这两者；

此时如果 $j < a[i]$，则 $dp[i][j]$ 不能由状态 $dp[i - 1][j - a[i]]$（该状态此时不存在）确定，如果 $j < b[i]$，则 $dp[i][j]$ 不能由状态 $dp[i - 1][j - b[i]]$（该状态不存在）确定，不难想象，若 $j < a[i]$ 且 $j < b[i]$，则 $dp[i][j]$ 为 $\inf$（用有限状态机的观点来考虑，可以认为该状态不可达）。

否则，$dp[i][j]$ 由且只由 $dp[i - 1][j - a[i]]$ 和 $dp[i - 1][j - b[i]]$ 这两个状态中那些存在中的状态确定。如果存在中的所有状态（最多两个）最小旋转次数的值都为 $\inf$，则转移方程确定 $dp[i][j]$ 为 $\inf$（即该状态不可达），而事实上，由二维 $dp$ 数组的含义来看 $dp[i][j]$ 也确实应该不可达；如果其中一个存在状态的值不为 $\inf$，则 $dp[i][j]$ 一定被更新为一个有限数（更新规则由转移方程确定）。

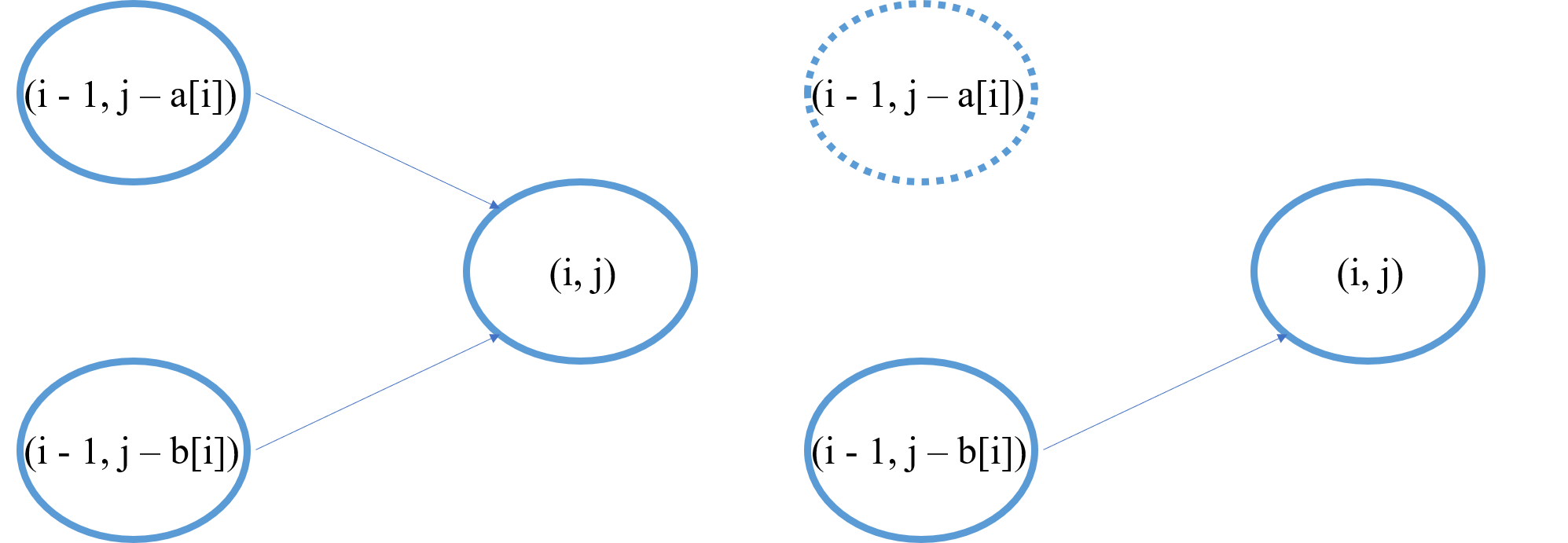
为了编写程序，可将状态转移方程写成以下等价形式：

$$dp[i][j] = \left\{ \begin{aligned} & \min (dp[i][j], dp[i - 1][j - a[i]]), & if (j >= a[i]) \\ & \min (dp[i][j], dp[i - 1][j - b[i]] + 1), & if (j >= b[i]) \end{aligned} \right.$$

易证两个状态转移方程的等价性（程序第一次更新 $dp[i][j]$ 时，该值一定为 $\inf$）。

程序：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int N = 1000;
const int INF = 1e8;
int a[N + 10], b[N + 10], dp[N + 10][6 * N + 10];

int main()
{
    int n;
    scanf("%d", &n);
    int s = 0;
    for (int i = 1; i <= n; i++) {
        scanf("%d%d", &a[i], &b[i]);
        s += a[i] + b[i];
    }
    // 状态矩阵初始化
    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= 6 * n; j++) dp[i][j] = INF;
    dp[1][b[1]] = 1; dp[1][a[1]] = 0;
    for (int i = 2; i <= n; i++) {
        for (int j = 0; j <= 6 * n; j++) {
            // 状态转移方程
            if (j - a[i] >= 0) dp[i][j] = min(dp[i][j], dp[i - 1][j - a[i]]);
            if (j - b[i] >= 0) dp[i][j] = min(dp[i][j], dp[i - 1][j - b[i]] + 1);
        }
    }
    int minD = INF, minT = INF;  //minD是最小差值，minT是最小交换次数
    for (int i = 0; i <= s; i++) {
        if (dp[n][i] != INF) {
            if (abs(i - (s - i)) < minD) {
                minD = abs(i - (s - i)); minT = dp[n][i];
            }
            else if (abs(i - (s - i)) == minD) minT = min(minT, dp[n][i]);
        }
    }
    printf("%d", minT);
    return 0;
}