快速排序算法（三种分区方法要熟练！）
快排确实厉害！！！
总的思想是分治递归，取定一个值作为标签，比该值小的去左边，比该值大的去右边。
单向扫描分区法：
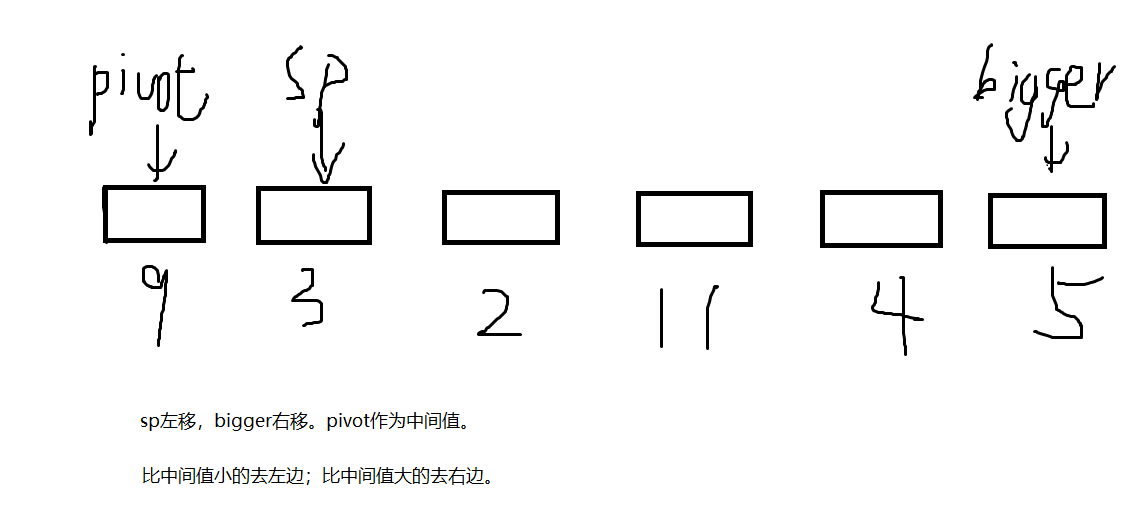
去左边的操作：只将sp++即可。
去右边的操作：具体是将sp指向的值与bigger指向的值交换。
考虑边界：当扫描指针sp与bigger相等时，再执行一次循环后，sp刚好在bigger的右边一格。
1 /* 2 * 快速排序算法 3 */ 4 void swp(int arr[], int n, int m) 5 { 6 int temp = arr[n]; 7 arr[n] = arr[m]; 8 arr[m] = temp; 9 } 10 int Part(int arr[], int p, int r) 11 { 12 int pivot = arr[p]; // 定中间数 13 int sp = p + 1; // 扫描指针 14 int bigger = r; // 右侧指针 15 while (sp <= bigger) 16 { 17 if (arr[sp] > pivot) { 18 swp(arr, sp, bigger); 19 bigger--; 20 } 21 else 22 sp++; 23 } 24 swp(arr, p, bigger); 25 return bigger; 26 } 27 void quickSort(int arr[], int p, int r) 28 { 29 int q = 0; 30 if (p < r) { 31 // 分区：小于的数移动到左边，大于的数移动到右边 32 q = Part(arr, p, r); 33 // 将排序问题分治 34 quickSort(arr, p, q - 1); 35 quickSort(arr, q + 1, r); 36 } 37 } 38 int main() 39 { 40 int ar[2] = {1, -1}; 41 quickSort(ar, 0, 1); 42 // 打印 43 for (int i = 0; i <= 1; i++) 44 cout << ar[i] << endl; 45 return 0; 46 }
双向扫描分区法：
与单向扫描分区类似，但left指针一直往右移，直到大于中间值时停止；right指针一直往左移，直到小于中间值时停止。然后left值与right值交换。之后left继续一直左移，right一直右移。重复执行。
小心：left一直左移（或right一直右移）导致的数组越界问题。
1 /* 2 * 快速排序算法 3 */ 4 void swp(int arr[], int n, int m) 5 { 6 int temp = arr[n]; 7 arr[n] = arr[m]; 8 arr[m] = temp; 9 } 10 int Part(int arr[], int p, int r) 11 { 12 int pivot = arr[p]; // 定中间数 13 int left = p + 1; // 左指针 14 int right = r; // 右指针 15 // 双向扫描核心 16 while (left <= right) 17 { 18 while (left <= right && arr[left] <= pivot) left++; 19 while (left <= right && arr[right] > pivot) right--; 20 if (left < right) 21 swp(arr, left, right); 22 } 23 swp(arr, p, right); 24 return right; 25 } 26 void quickSort(int arr[], int p, int r) 27 { 28 int q = 0; 29 if (p < r) { 30 // 分区：小于等于的数移动到左边，大于的数移动到右边 31 q = Part(arr, p, r); 32 // 将排序问题分治 33 quickSort(arr, p, q - 1); 34 quickSort(arr, q + 1, r); 35 } 36 } 37 int main() 38 { 39 int ar[8] = {2, 3, 3, 3, 45, 8, 4, 6}; 40 quickSort(ar, 0, 7); 41 // 打印 42 for (int i = 0; i <= 7; i++) 43 cout << ar[i] << " "; 44 return 0; 45 }
三指针分区法：
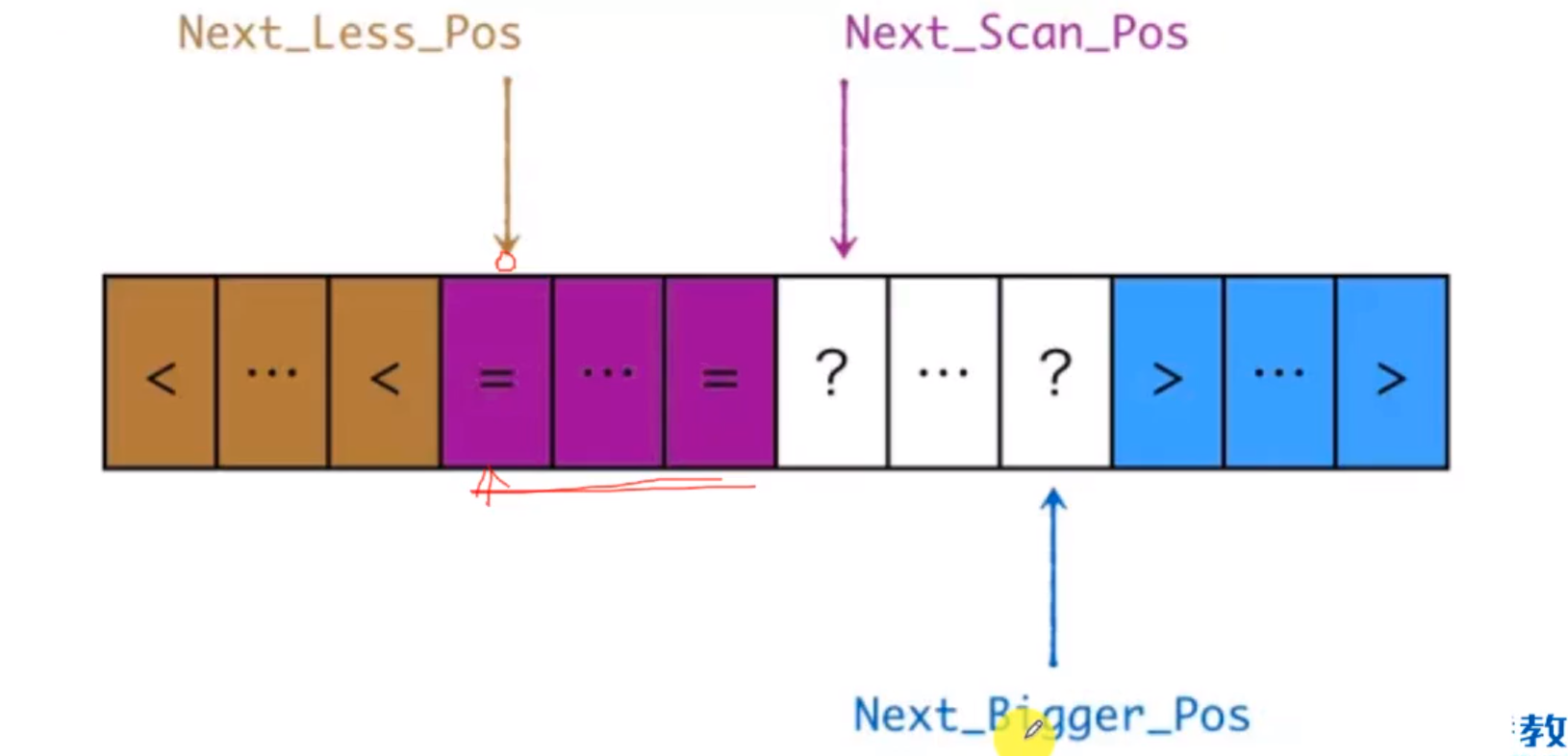
三指针分区法对于相等元素较多的数组能提升一定的效率。
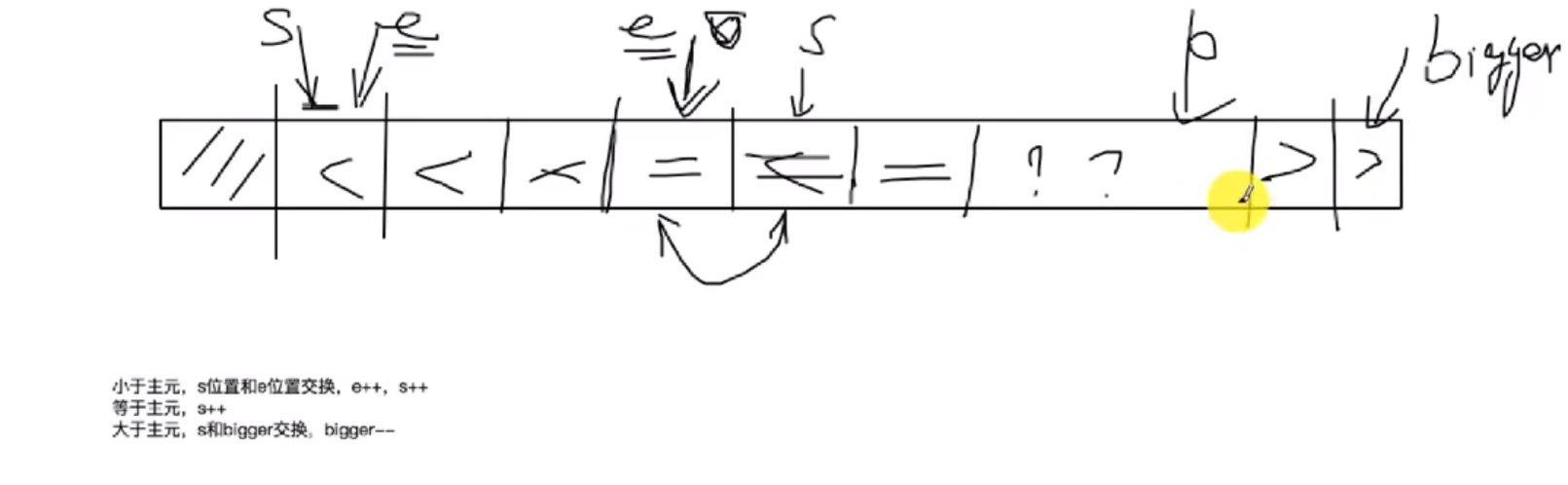
Next_Less_Pos指针始终指向数组的相等区第一个元素；Next_Scan_Pos指针始终指向要扫描区域的第一个元素；Next_Bigger_Pos指针的右区域所有元素总大于主元。
1 /* 2 * 快速排序算法 3 */ 4 void swp(int arr[], int n, int m) 5 { 6 int temp = arr[n]; 7 arr[n] = arr[m]; 8 arr[m] = temp; 9 } 10 void Part(int arr[], int p, int &e, int &bigger) 11 { 12 int pivot = arr[p]; // 定中间数 13 int s = e; 14 // 三指针分区核心 15 while (s <= bigger) { 16 if (arr[s] < pivot) { 17 swp(arr, s, e); 18 s++; e++; 19 } 20 else if (arr[s] > pivot) { 21 swp(arr, s, bigger); 22 bigger--; 23 } 24 else s++; 25 } 26 swp(arr, e - 1, p); 27 } 28 void quickSort(int arr[], int p, int r) 29 { 30 int left = p + 1, right = r; 31 if (p < r) { 32 // 分区：小于的数移动到左边，大于的数移动到右边，等于的数在中间 33 Part(arr, p, left, right); 34 // 将排序问题分治 35 if (left > p) quickSort(arr, p, left - 1); 36 if (right < r) quickSort(arr, right + 1, r); 37 } 38 } 39 int main() 40 { 41 int ar[20]; 42 srand((unsigned)time(nullptr)); 43 for (int i = 0; i <= 19; i++) 44 ar[i] = rand() % (10 - 1 + 1) + 1; 45 quickSort(ar, 0, 19); 46 // 打印 47 for (int i = 0; i <= 19; i++) 48 cout << ar[i] << " "; 49 return 0; 50 }
小心边界：必须是相等区域的前一个小于元素，和相等区域的后一个大于元素（即 left - 1 和 right + 1），这时能避免无限循环。
但在避免无限循环的同时，又得保证边界下标的合理性，故我们此时加 if 语句判断。
补充 工程实践中的一些优化：
- 三点中值法（去首元素、尾元素和中间元素，取三元素的中间值作为主元）
- 绝对中值法（花费 O(n) 的时间，寻找中间值作为主元）
- 部分插入排序（在递归树中，对于元素较少的部分直接用插入排序）
