有限差分法求导
数字图像处理中，经常遇到求导的情况，但是我们的数字图像都是离散变量，因此无法直接对其求导，我们只能对其近似求导，所以此时我们可以采用有限差分求导对其近似求解
有限差分法以变量离散取值后对应的函数值来近似微分方程中独立变量的连续取值。在有限差分方法中，我们放弃了微分方程中独立变量可以取连续值的特征，而关注独立变量离散取值后对应的函数值。但是从原则上说，这种方法仍然可以达到任意满意的计算精度。因为方程的连续数值解可以通过减小独立变量离散取值的间格，或者通过离散点上的函数值插值计算来近似得到。这种方法是随着计算机的诞生和应用而发展起来的。其计算格式和程序的设计都比较直观和简单，因而，它在计算数学中使用广泛。
有限差分法的具体操作分为两个部分：
1. 用差分代替微分方程中的微分，将连续变化的变量离散化，从而得到差分方程组的数学形式；
2. 求解差分方程组。
首先我们直接给出结果，然后在后面进行公式推导：
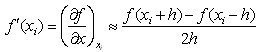
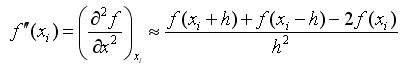
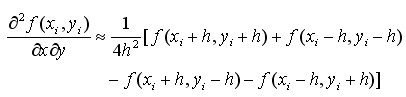
推导过程：
我们知道任一f(x)均可将其展开成泰勒公式：
一阶泰勒公式展开式为：
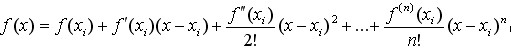（1）
我们将f(xi+h)和f(xi-h)均用泰勒公式展开：
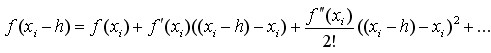（2）
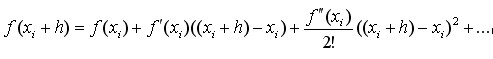（3）
将（1）和（2）相减，整理可得：
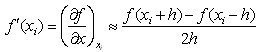（4）
即证
同理可证 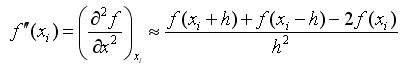（5）
同样我们可以利用二阶泰勒公式的展开式推出：
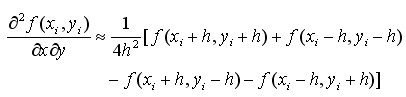（6）
二阶泰勒公式的展开式为：
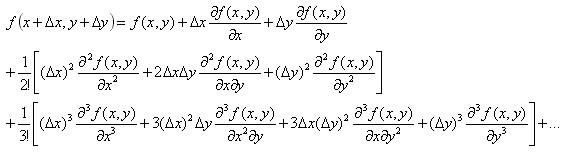（7）
