浅谈强连通分量（Tarjan）

强连通分量\(\rm （Tarjan）\)

            ——作者：BiuBiu_Miku

\(1.\)一些术语

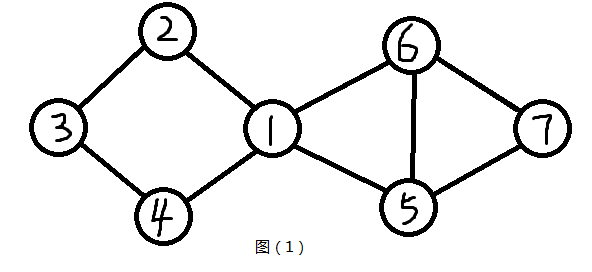
  · 无向图:指的是一张图里面所有的边都是双向的，好比两个人打电话 \(U\) 可以打给 \(V\) 同时 \(V\) 也可以打给 \(U\)（ 如图1 就是一个无向图）

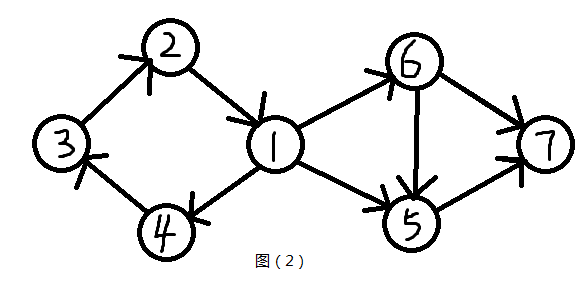
  · 有向图:指的是一张图里面所有的边都是单向的，好比一条单向的公路只能从 \(U→V\) 而不能从 \(V→U\) （ 如图2 就是一个有向图）

  · 连通:指的是在 \(\rm \color{red}{无向图}\) 中，任意节点 \(V\) 可以到达任意节点 \(U\) ， 如图1 中点 \(1\) 和点 \(2\) 可以互相到达 ，所以点 \(1\) 和点 \(2\) 是联通的

  · 强连通:指在 \(\rm \color{red}{有向图}\) 中，某两个点可以互相到达，比 如图2 中 点 \(1\) 和点 \(2\) 就是可以互相到达对方的,虽然不是直接到达，但是可以到达，就将其称为强连通

  · 弱连通:指在 \(\rm \color{red}{有向图}\) 中，某两个点若本身不存在强连通关系，但是通过将其看成 \(\rm \color{red}{无向图}\) 使其连通，则将他们称为弱连通

  · 强连通分量:指在 \(\rm \color{red}{有向图}\) 中,一些节点存在强连通关系，如图(2) 中节点 \(1,2,3,4\) , 节点 \(5\) , 节点 \(6\) , 节点 \(7\) 分别为图中的四个强连通分量，强连通分量也可以是单独一个节点

\(2.\)\(\rm Tarjan\)算法的思想简述:

  · 我们定义两个变量：

     \(dfn[i]\) 表示节点 \(i\) 的时间戳（也就是dfs后序遍历的顺序）

     \(low[i]\) 表示节点 \(i\) 可以通过一些节点找到比自己时间戳早的时间戳

       比如说节点 \(U\) 的时间戳 \((dfn[U])\) 是 \(1\)，节点 \(V\) 的时间戳是 \(3\) ，\(V\) 可以到达 \(U\) 则 \(V\) 的 \(low[V]\) 就是 \(1\)

  · 关于此算法的流程:

    \(\rm Tarjan\) 算法是一个通过对图进行深度优先搜索并通过同时维护一个栈以及两个相关时间戳 (上面提到的两个变量) 的算法。

    第一步:建图

      可以用邻接矩阵，链式前向星，或者其他东西

      \(\rm \color{red}{PS:一定是单向边}\)

    第二步:跑图

      用 \(dfs\) 从一个节点开始遍历整张图，与此同时更新时间戳。

      在 \(dfs\) 过程中每遍历到一个元素，就将其存到栈中，其主要维护的是上文提到的 \(low\) ， 因为 \(dfn\) 是 \(dfs\) 的搜索顺序的时间戳，所以从有值之后基本上就不用变化了，而 \(low\) 不能被马上确定，因为在 \(dfs\) 的遍历中，也许当前节点可以到达比当前的 \(low\) 更前的节点，此时我们就要更新他的 \(low\) 变为更前的节点的遍历时间，也就是 \(dfn\) 。

    第三步:存强连通分量

      当我们搜索完之后，发现某个节点的 \(dfn\) 和 \(low\) 相等时，说明我们找到了一个强连通分量，因为当前节点不能再到达比自己更小的节点了，那么此时，以这个节点为 \(low\) 值得节点自然不会再次被更新了，因为他是按 \(dfs\) 以后序遍历，顺序搜索过来的，因此我们此时就可以开始存强连通分量了，其手段是利用栈将栈首元素进行存储，之后弹出，直到栈首元素为当前点的值为止

      我们可以以染色的手段来存储强连通分量，每当找到一个强连通分量，就可以将其的每一个值作为下标，在数组 \(color\) 中进行染色，其存储的值一般为找到的强连通分量的编号，如：假设我找到了一个强连通分量为 \(7,8,9\) ，其又是第二个被找到的强连通分量，则将 \(color[7] color[8] color[9]\) 标为 \(2\)。

\(3.\)\(\rm Tarjan\)算法的代码实现:

    题目:在一个有向图中，有n个节点，m条边，现给出这m条边，请输出图中所有的强连通分量。

\(\rm Code:\)

#include<bits/stdc++.h>
using namespace std;
int n,m;                        
struct edge{                        //定义存边的变量
	int from,to,next;
} e[10005];
int head[10005];
int cnt;
void Insert(int x,int y){            //链式前向星存边
	e[++cnt].from=x;
	e[cnt].to=y;
	e[cnt].next=head[x];
	head[x]=cnt;
}
int dfn[10005];            //上文提到的dfn
int low[10005];            //上文提到的low
int t;                     //当前搜索的时间，用于给时间戳dfn与low赋初始值
stack<int> s;            
int p[100005];            //判断某个元素在不在栈里面
// int tot;
// int color[100005];
void Tarjan(int now){
	s.push(now);            //讲当前元素放入栈
	dfn[now]=low[now]=++t;      //讲当前搜索的时间，也就是当前搜过了几个点的数量赋值给时间戳dfn,同时对low进行初始化
        p[s.top()]=true;
	for(int i=head[now];i;i=e[i].next){      //链式前向星遍历所有节点
		int get=e[i].to;            
		if(!dfn[get]){            //判断当前节点有没有被搜索过
			Tarjan(get);      //如果没有，那就搜这个节点
			low[now]=min(low[now],low[get]);      //更新当前节点的low，为什么不是 low[now]=min(low[now],dfn[get]); 呢？我们不妨观察一下，low的值是不是永远≤dfn的？此时既然now可以到达get，那么now自然也可以到达get节点能到达的节点
            	}
		else if(p[get]) low[now]=min(low[now],dfn[get]);      //否则判断当前节点在不在栈里，如果不在，就不用理他，如果在那么就可以更新一下当前节点，因为当前节点可以到达get,但此时的low不一定是最终得到的值,所以不能写low[now]=min(low[now],low[get]);   
	}
	if(dfn[now]==low[now]){            //如果两个相等，说明当前节点不能再更新了，不能再找到比自己low更小的值
		// tot++;
                while(s.top()!=now){            //将栈首到当前元素的所有值弹出队列，说明这堆东西就是一个强连通分量
			printf("%d ",s.top());	
                        // color[s.top()]=tot;
			p[s.top()]=false;            //标记其不在栈里
			s.pop();
		}
		printf("%d",s.top());	      //因为只是弹到当前节点，当前节点也是包含在这个强连通分量内的，所以再做一次
                // color[s.top()]=tot;
		p[s.top()]=false;
		s.pop();
		
		printf("\n");
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		int x,y;
		scanf("%d%d",&x,&y);
		Insert(x,y);           //存边
	}
	for(int i=1;i<=n;i++)            //因为图不一定保证是连通的，有可能某个节点不被其他任何节点到达，所以要用for判断一遍如果没有被搜过就搜，搜过了就没他什么事了
		if(!dfn[i])
			Tarjan(i);

	return 0;
}

\(4.\)强连通分量的应用:

  · 缩点

     因为强连通分量一般为一个环，所以在一些题目中，我们可以把这些环变成一个点来简便搜索，然后把缩小后的点再次连接，建一张新的图，然后开始一系列操作。

     参考例题:洛谷 P3387【模板】缩点

\(\rm Code:\)

#include<bits/stdc++.h>
#define MAXN 100005
using namespace std;
long long n,m;
struct edge{
	long long from,to,next;
} e[MAXN];
long long head[MAXN];
long long cnt;
long long qlt;
void Insert(long long x,long long y){
	e[++cnt].from=x;
	e[cnt].to=y;
	e[cnt].next=head[x];
	head[x]=cnt;
}
long long dfn[MAXN];
long long low[MAXN];
long long t;
stack<int> s;
long long p[MAXN];
long long color[MAXN];
long long f[MAXN];
long long u[MAXN],v[MAXN],l[MAXN];
long long dis[MAXN];
long long mmax;
const long long oo=0x7f7f7f;
void Tarjan(long long now){
	s.push(now);
	dfn[now]=low[now]=++t;
	p[now]=false;
	for(long long i=head[now];i;i=e[i].next){
		long long get=e[i].to;
		if(!dfn[get]){
			Tarjan(get);
			low[now]=min(low[now],low[get]);
		}
		else if(!p[get]) low[now]=min(low[now],dfn[get]);
	}
	if(dfn[now]==low[now]){
		qlt++;
		while(s.top()!=now){
			color[s.top()]=qlt; 
			p[s.top()]=true;
			f[qlt]+=l[s.top()];            //存储缩点后单点的点权
			s.pop();
	 	}
		color[s.top()]=qlt; 
		p[s.top()]=true;
		f[qlt]+=l[s.top()];            //同上，再做一次
		s.pop();
	}
}
void dfs(long long now) {      //做一遍记忆化搜索来更新从某一个节点的答案(这里也可以用最短路算法来实现)
	dis[now]=f[now];            //初始化，自己的点权就是自己
	long long mmmax=0;
	for(long long i=head[now];i;i=e[i].next){      //遍历每个节点
		long long get=e[i].to;            
		if(!dis[get])dfs(get);            //如果节点没被搜过就搜
		mmmax=max(mmmax,dis[get]);         //更新最大值
	}
	dis[now]+=mmmax;            //更新当前值
}
int main(){
	scanf("%lld%lld",&n,&m);
	for(long long i=1;i<=n;i++) scanf("%lld",&l[i]);
	for(long long i=1;i<=m;i++){
		scanf("%lld%lld",&u[i],&v[i]);
		Insert(u[i],v[i]);
	}
	for(long long i=1;i<=n;i++)
		if(!dfn[i])
			Tarjan(i);
	memset(e,0,sizeof(e));                  //清零重新建图
	memset(head,0,sizeof(head));
	cnt=0; 
	for(long long i=1;i<=m;i++)
		if(color[u[i]]!=color[v[i]])                  //建立缩点后的图，如果两点不在同一个强连通分量里，说明两个集合不连通，所以将其连通
			Insert(color[u[i]],color[v[i]]);
	for(long long i=1;i<=qlt;i++)
		if(!dis[i]){
			dfs(i);                            //如果当前节点没被搜过，就进行记忆化搜索
			mmax=max(dis[i],mmax);            //更新最大值
		}
	printf("%lld\n",mmax);                        //输出答案
	return 0;
}

感谢您的阅读，如大佬有什么建议或本文有什么错误欢迎指出，感谢大佬%%%