关于二元插值问题的探讨
前言
最近数值分析课上老师给出一道作业题,题目的内容为:
某地区为估计某矿物的储量,在该地区内进行勘探,得到如下数据:
| 编号 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 |
| x坐标/km | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 |
| y坐标/km | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 |
|
矿物体 厚度H/m |
13.72 | 25.80 | 8.47 | 25.27 | 22.32 | 15.47 | 21.33 | 14.49 | 24.83 | 26.19 |
| 编号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| x坐标/km | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 |
| y坐标/km | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 |
|
矿物体 厚度H/m |
23.28 | 26.48 | 29.14 | 12.04 | 14.58 | 19.95 | 23.73 | 15.35 | 18.01 | 16.29 |
试估计出此地区内($1<x<4,1<y<5$ )该矿物的储量。
老师还给了提示:矿物体的厚度$H$是坐标$x,y$的二元函数,即面密度函数为:$H = H(x, y) $, 根据二重积分可知,所求矿物的储量就是求二重积分$\iint\limits_{D}H\left ( x,y\right )dxdy$的值,其中$D=\left \{\left ( x,y\right )|1\leqslant x\leqslant 4,1\leqslant y\leqslant 5\right \}$。可考虑将二重积分化为累次积分,利用复合求积公式计算。(不相信我们的实力哈哈😉)大家看着这道题目会怎么去做呢?
一、二元拉格朗日插值
我首先想到的是用类似于一元拉格朗日插值的二元插值来对数据进行插值计算,得出一个形如$\sum_{i}^{m}\sum_{j}^{n}a_{ij}x^{i}y^{j}$的二元函数,再对这个函数进行累次积分即可得出结果。根据一元拉格朗日插值可推测二元拉格朗日插值具有类似的形式:
![]()
其中,$f\left ( x_i,y_j \right )$为$\left ( x_i,y_j \right )$处表格中的值,$\sigma _i\left ( x \right )=\left ( x-x_0\right )\cdots \left ( x-x_{i-1}\right )\left ( x-x_{i+1}\right )\cdots \left ( x-x_m\right )$,$\omega _j\left ( y \right )=\left ( y-y_0\right )\cdots \left ( y-y_{j-1}\right )\left ( y-y_{j+1}\right )\cdots \left ( y-y_n\right )$。这里我使用c#编程语言使用WinForm连接Mathematica来设计算法:
//二元插值函数
public void BinaryInterpolation(string[] xdatastr, string[] ydatastr, string[] zdatastr)
{
string messagestr = "";
string pictpathstr = Directory.GetCurrentDirectory().ToString() + "\\images\\picture_" + imagenumber + ".png";
mathKernel1.CaptureMessages = true;
mathKernel1.CaptureGraphics = true;
mathKernel1.GraphicsHeight = pictureBox1.Height;
mathKernel1.GraphicsWidth = pictureBox1.Width;
mathKernel1.Compute("ExportString[SetPrecision[Expand[Simplify[{xdata = " + ArrayToTableFunction(xdatastr, 1) + ", ydata = " + ArrayToTableFunction(ydatastr, 1) + ", zdata = " + ArrayToTableFunction(zdatastr, ydatastr.Length) + ", Ln = 0, For[m = 1, m <= " + xdatastr.Length + ", m++, {\\[Sigma] = 1, \\[Sigma]k = 1, For[i = 1, i <= " + xdatastr.Length + ", i++, If[i != m, {\\[Sigma] = \\[Sigma] * (x - xdata[[i]]), \\[Sigma]k = \\[Sigma]k * (xdata[[m]] - xdata[[i]])}]], For[n = 1, n <= " + ydatastr.Length + ", n++, {\\[Omega] = 1, \\[Omega]k = 1, For[j = 1, j <= " + ydatastr.Length + ", j++, If[j != n, {\\[Omega] = \\[Omega] * (y - ydata[[j]]), \\[Omega]k = \\[Omega]k * (ydata[[n]] - ydata[[j]])}]], Ln = Ln + zdata[[m, n]]*\\[Sigma]/\\[Sigma]k*\\[Omega]/\\[Omega]k}]}], Ln}[[6]][[1]]]]," + significantdigits + "], \"MathML\"]");
result = mathKernel1.Result.ToString();
mathMLControl1.MC_loadXML(result);
foreach (string me in mathKernel1.Messages)
{
messagestr += me;
}
textBox4.Text = messagestr;
}
//将数组转化为列表
public string ArrayToTableFunction(string[] data1, string[] data2)
{
StringBuilder outputstr = new StringBuilder();
outputstr.Append("{");
for (int i = 0; i < data1.Length; i++)
{
if (i == data1.Length - 1)
{
outputstr.Append("{" + data1[i] + "," + data2[i] + "}");
}
else
{
outputstr.Append("{" + data1[i] + "," + data2[i] + "},");
}
}
outputstr.Append("}");
return outputstr.ToString();
}程序运行结果如下:
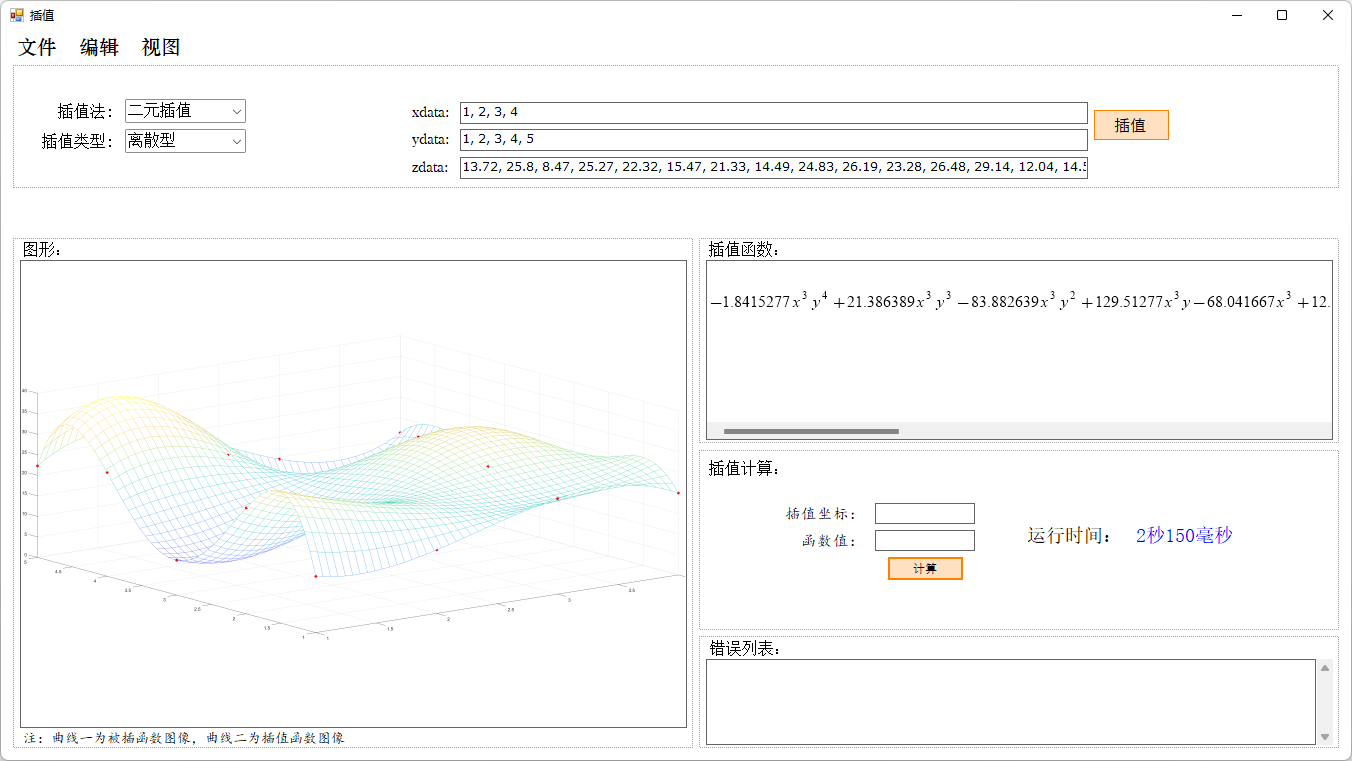
插值得出的函数为$-1.8415277x^3y^4 + 21.386389x^3y^3 - 83.882639x^3y^2 + 129.51277x^3y - 68.041667x^3 + 12.159166x^2y^4 - 140.705x^2y^3 + 548.72833x^2y^2 - 841.5375x^2y + 441.585x^2 - 21.029305xy^4 + 241.22527xy^3 - 927.47903xy^2 + 1397.153xy - 728.74333x + 5.8191667y^4 - 62.391667y^3 + 213.15083y^2 - 267.81833y + 146.47$
其图像为:
对插值函数分别对$x$和$y$积分可得结果为252.193。
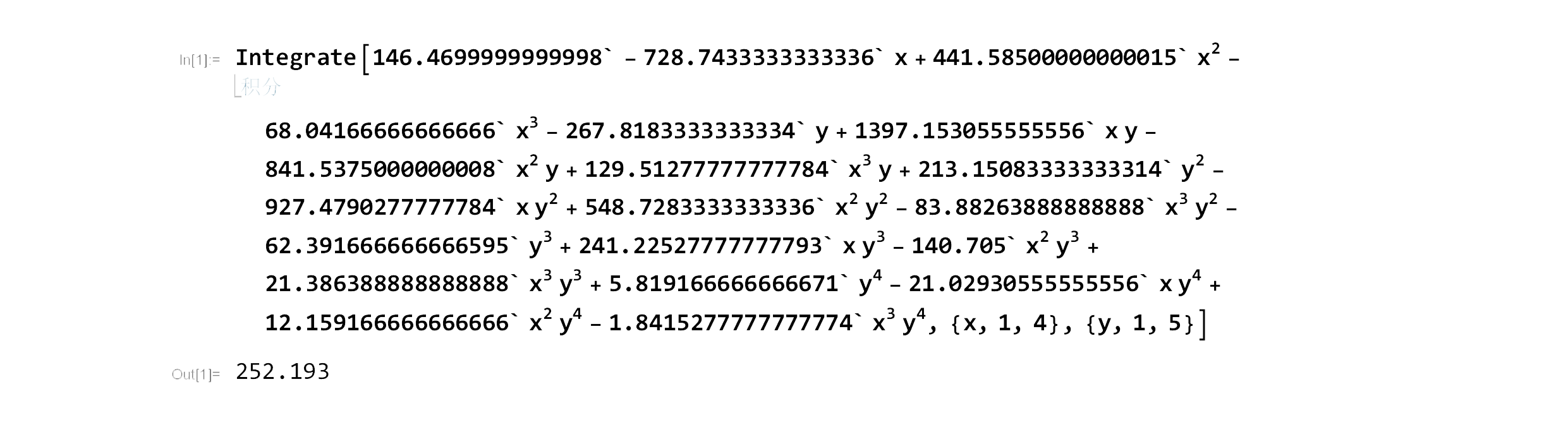
二、累次拉格朗日插值
做完二元插值,我突然想到,既然积分有重积分和累次积分,那么类似于累次积分,拉格朗日插值可否累次进行呢?带着这个疑问,我开始进行了实验:首先将表格写成$x,y$坐标形式如下
| x/y | 1 | 2 | 3 | 4 | 5 |
| 1 | 13.72 | 25.80 | 8.47 | 25.27 | 22.32 |
| 2 | 15.47 | 21.33 | 14.49 | 24.83 | 26.19 |
| 3 | 23.28 | 26.48 | 29.14 | 12.04 | 14.58 |
| 4 | 19.95 | 23.73 | 15.35 | 18.01 | 16.29 |
分别对每一行进行一元插值,得出的插值函数对$y$进行积分,可以得到与$x$对应的积分结果,然后再对结果进行一元插值并对$x$积分得出最终结果。利用程序实现:
//累次拉格朗日插值函数
public void LagrangePointSetsNIntegrationForm(string[] xdatastr, string[] ydatastr, string[] zdatastr)
{
string messagestr = "";
string[] firstintrgrate = new string[xdatastr.Length];
string[][] zdatameshgrid = new string[xdatastr.Length][];
mathKernel1.CaptureMessages = true;
for (int i = 0; i < xdatastr.Length; i++)
{
zdatameshgrid[i] = new string[ydatastr.Length];
}
for (int n = 0; n < zdatastr.Length; n++)
{
zdatameshgrid[n / ydatastr.Length][n % ydatastr.Length] = zdatastr[n];
}
for (int i = 0; i < xdatastr.Length; i++)
{
mathKernel1.Compute("Integrate[Expand[Simplify[{xdata =" + ListToArrayFunction(ydatastr) + ",ydata = " + ListToArrayFunction(zdatameshgrid[i]) + ", Ln = 0, For[i = 1, i <= " + ydatastr.Length + ",i++, {\\[Omega] = 1, \\[Omega]k = 1, For[j = 1, j <= " + ydatastr.Length + ", j++, If[j != i, \\[Omega] = \\[Omega] * (x - xdata[[j]])]], For[k = 1, k <= " + ydatastr.Length + ", k++, If[k != i, \\[Omega]k = \\[Omega]k * (xdata[[i]] -xdata[[k]])]], Ln = Ln + ydata[[i]]*\\[Omega]/\\[Omega]k}], Ln}[[5]]]],{x, " + ydatastr[0] + ", " + ydatastr[ydatastr.Length - 1] + "}]");
firstintrgrate[i] = mathKernel1.Result.ToString();
textBox6.AppendText(mathKernel1.Result.ToString() + " ");
}
for (int j = 0; j < xdatastr.Length; j++)
{
mathKernel1.Compute("Integrate[Expand[Simplify[{xdata =" + ListToArrayFunction(xdatastr) + ",ydata = " + ListToArrayFunction(firstintrgrate) + ", Ln = 0, For[i = 1, i <= " + xdatastr.Length + ",i++, {\\[Omega] = 1, \\[Omega]k = 1, For[j = 1, j <= " + xdatastr.Length + ", j++, If[j != i, \\[Omega] = \\[Omega] * (x - xdata[[j]])]], For[k = 1, k <= " + xdatastr.Length + ", k++, If[k != i, \\[Omega]k = \\[Omega]k * (xdata[[i]] -xdata[[k]])]], Ln = Ln + ydata[[i]]*\\[Omega]/\\[Omega]k}], Ln}[[5]]]],{x, " + xdatastr[0] + ", " + xdatastr[xdatastr.Length - 1] + "}]");
textBox5.Text = mathKernel1.Result.ToString();
}
foreach (string me in mathKernel1.Messages)
{
messagestr += me;
}
}
//将列表转化为数组
public string ListToArrayFunction(string[] data)
{
StringBuilder outputstr = new StringBuilder();
outputstr.Append("{");
for (int i = 0; i < data.Length; i++)
{
if (i == data.Length - 1)
{
outputstr.Append(data[i]);
}
else
{
outputstr.Append(data[i] + ",");
}
}
outputstr.Append("}");
return outputstr.ToString();
}程序运行结果如下:
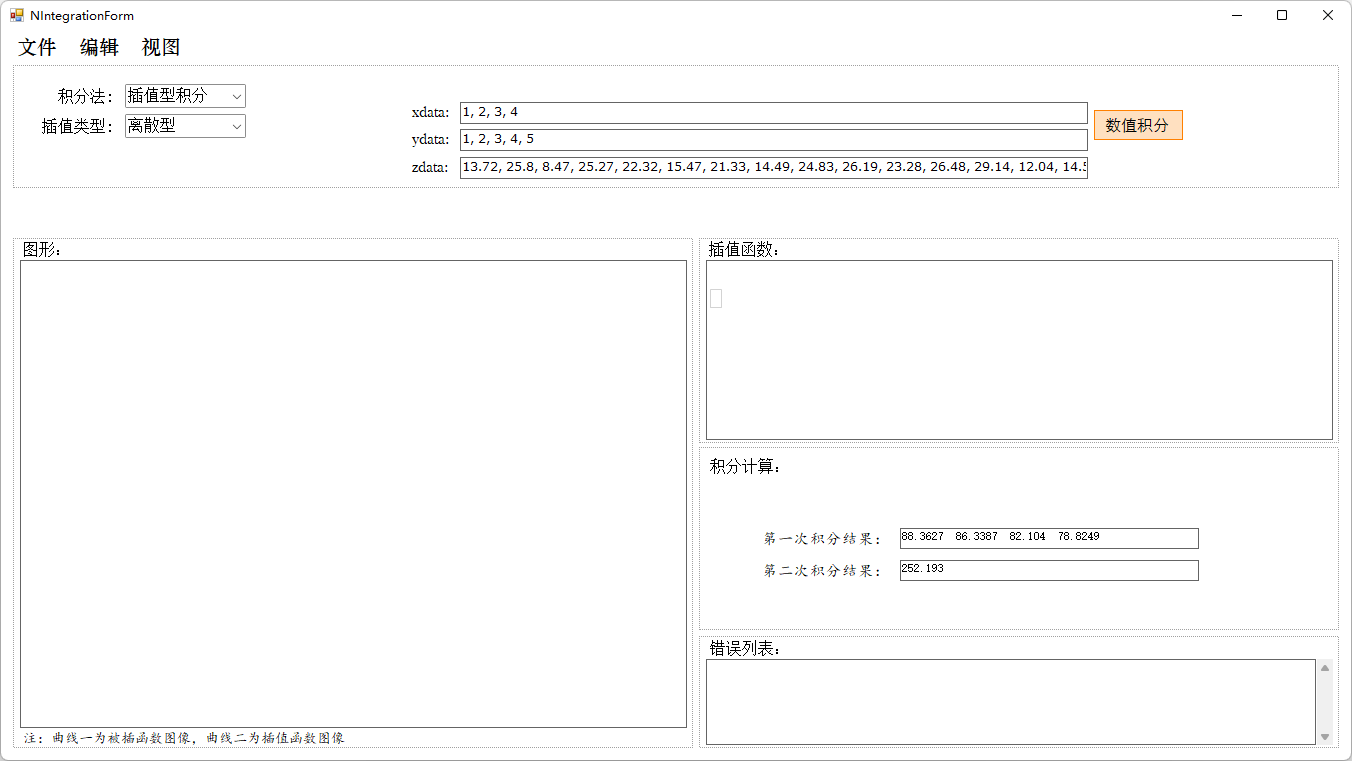
结果显示,累次进行的插值结果与二元插值结果是相同的。那如果我改变插值顺序,即先对$x$插值,再对$y$插值,结果会发生变化吗?我将数据表进行转置:
| y/x | 1 | 2 | 3 | 4 |
| 1 | 13.72 | 15.47 | 23.28 | 19.95 |
| 2 | 25.80 | 21.33 | 26.48 | 23.73 |
| 3 | 8.47 | 14.49 | 29.14 | 15.35 |
| 4 | 25.27 | 24.83 | 12.04 | 18.01 |
| 5 | 22.32 | 26.19 | 14.58 | 16.29 |
输入数据后运行程序:
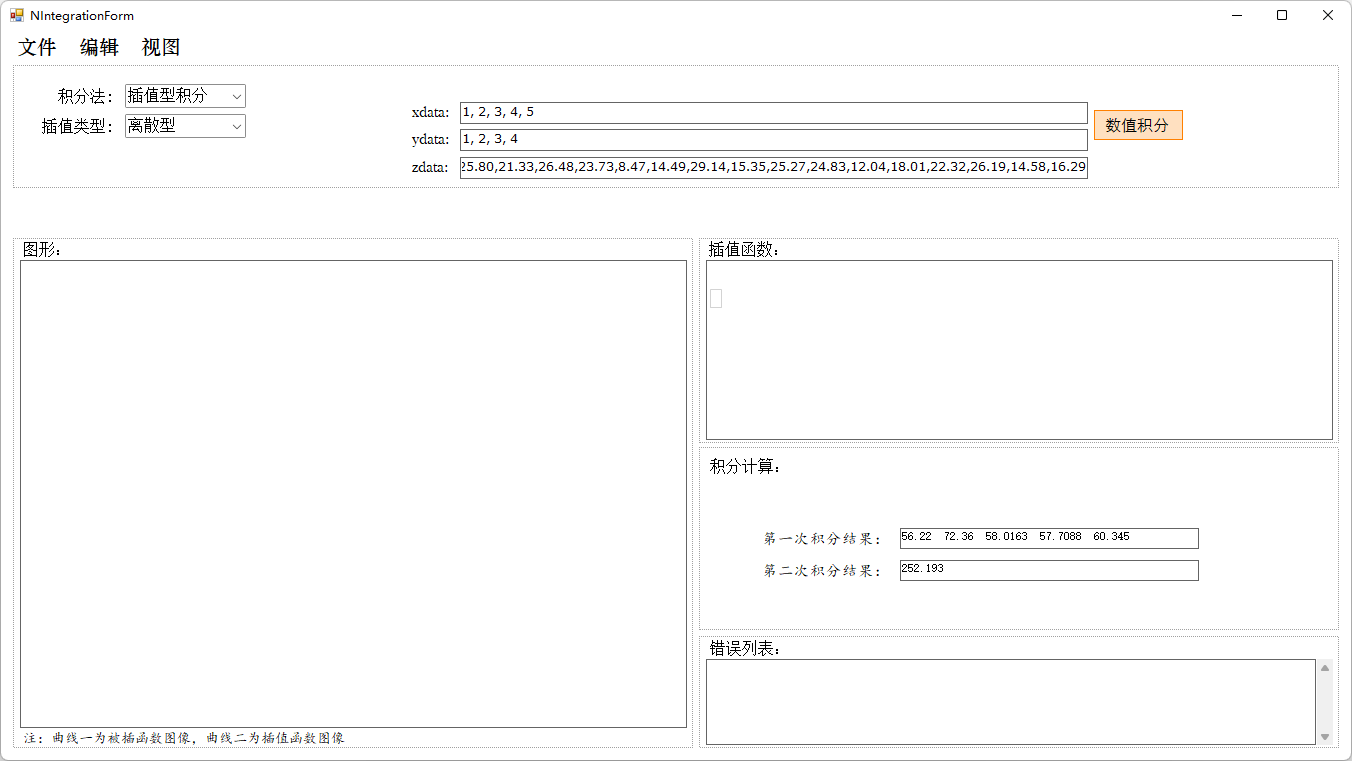
从结果上看,虽然插值的顺序不同,第一次的积分值不相同,但是第二次积分值确实相同的,为了避免偶然事件的影响,我已使用多组数据证实了这个结论的正确性。但遗憾的是,我暂时没有找到理论依据,无法给出证明。
三、结论
拉格朗日插值和积分一样,存在二维插值和累次插值,并且二者是相等的(可能需要满足某些条件)。虽然目前缺少理论依据,但是对于数学建模等的应用可以提供一个新方法。



