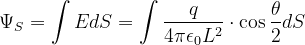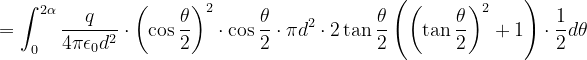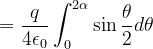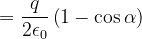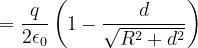利用定积分求某一点处电场强度

1.等式推导

　　在求电场强度之前需要用到一个关于球体分割面积的等式，即：用任意平面去截取一半径为R的球体，已知截后球面与圆心的夹角为θ，则所截取球面面积为：

　　

　　推导如下：

方法一：

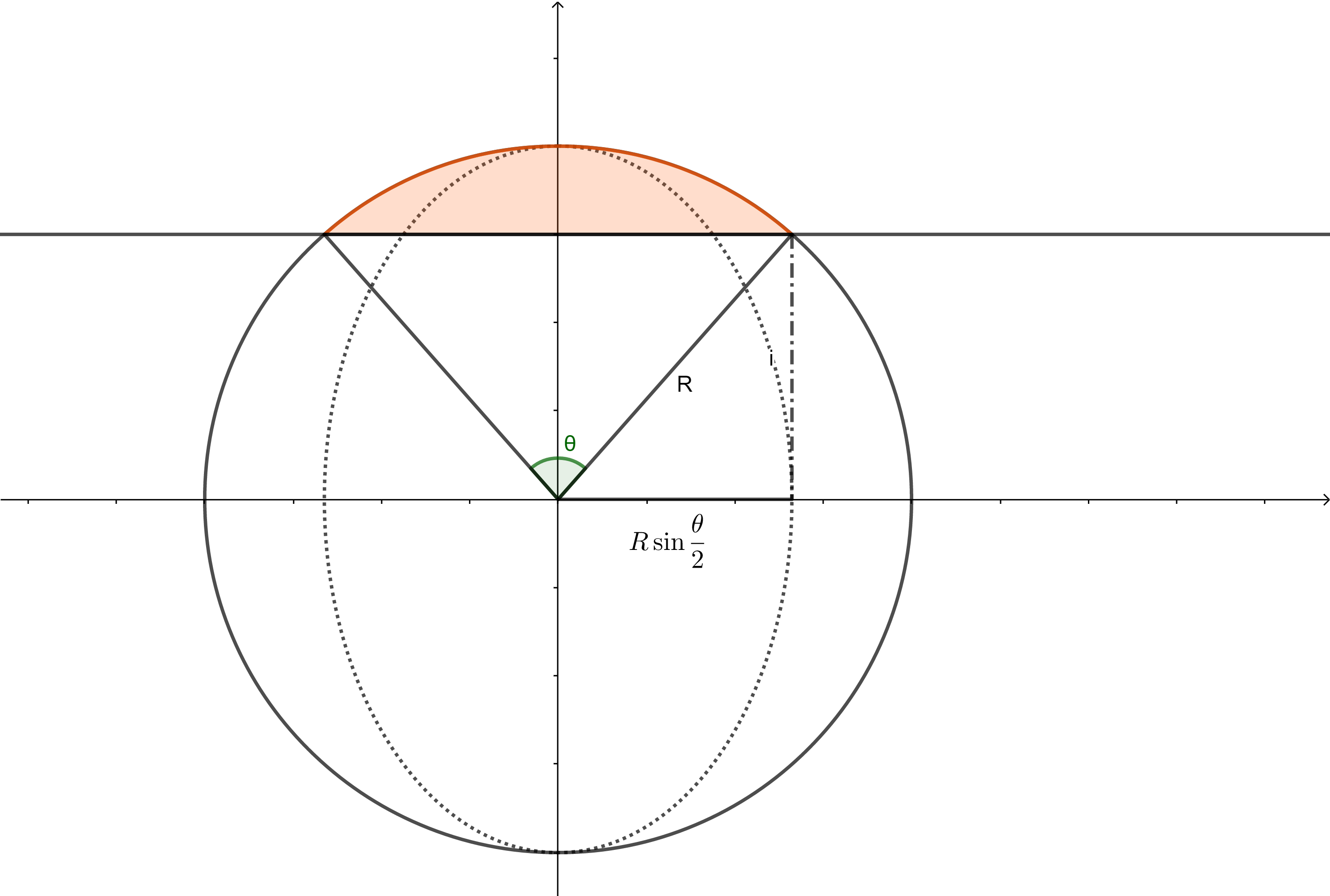
　　要求截取球面的面积，可用第一型曲面积分令被积函数为1即可得出。即：

   

　　

　　

　　

　　

　　

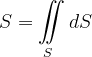
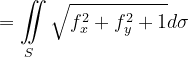
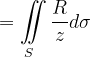
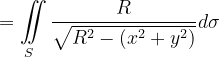
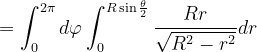
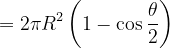
方法二：

　　利用旋转曲面的面积求所截球面的面积：

   

　　

　　

　　

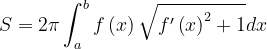
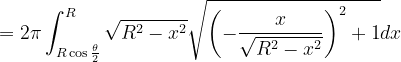
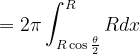
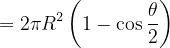
2.应用

1.

　　在真空中有一半径为R的均匀带电球面，总带电量为Q(Q>0)。今在球面上挖去非常小的一块面积△S(连同电荷)，且假设挖去后不影响原来的电荷分布，求挖去△S后球心处电场强度的大小和方向。

标准解法

解：设Q>0，电荷面密度为 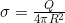,均匀带电的球面在球心处的电场强度为.

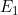　　在球面上挖去△S，相当于再使△S带电荷量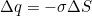.设△q在球心处的电场强度为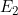.由电场强度的叠加原理可知，球心处的电场强度为

　　

　　由于球面的电荷均匀分布，在球心的电场强度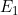=0.所以

　　

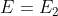
　　由于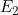是非常小的面积△S上的负电荷产生的，故可作点电荷电场处理，即

　　

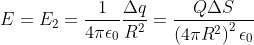
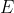　　 的方向指向△S处，指向x轴正方向。

个人解法

解：由球面截面面积等式：

　　

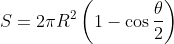
可得：

　　

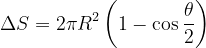
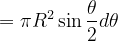
　　已知

 

　　则有

 

　　

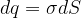
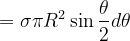
　　因此

  

　　

　　

　　

　　

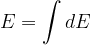
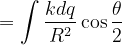
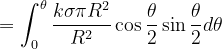
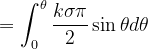
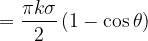
　　由

　　

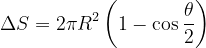
　　可得：

　　

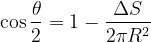
　　则

　　   

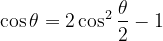
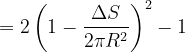
　　因此

　

　　

　　

　　

　　

　　

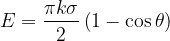
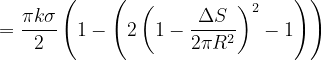
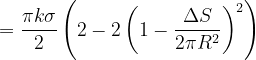
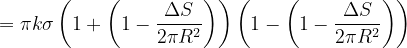
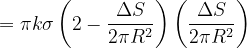
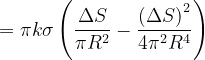
　　由于△S面积非常小，则舍去高阶无穷小量可得：

  

　　

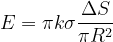
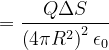
2.

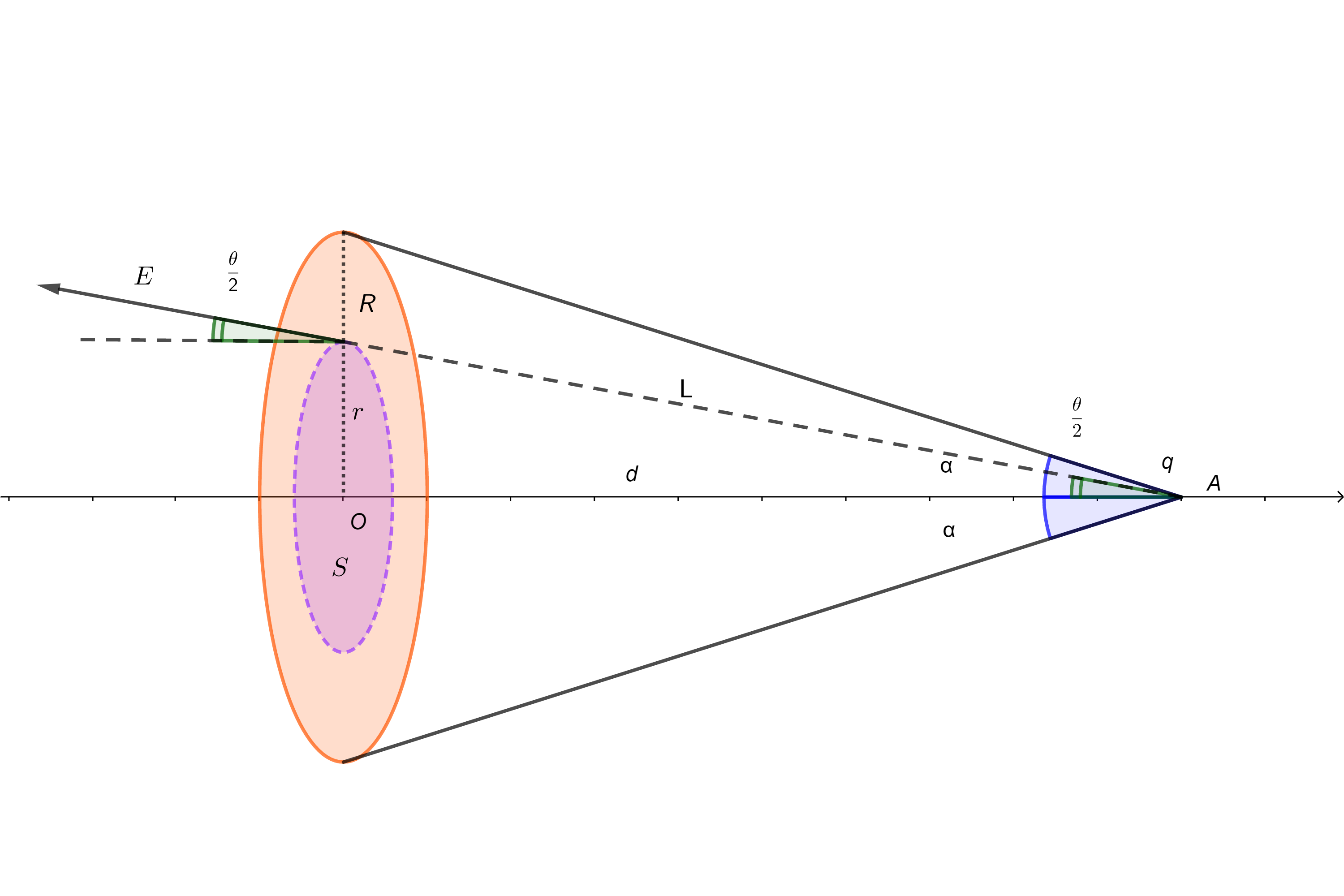
　　如图所示，在点电荷q的电场中，取半径为R的圆形平面。设q在垂直于平面并通过圆心O的轴线上点A处，点A与圆心点O的距离为d。试计算通过此平面的E通量。

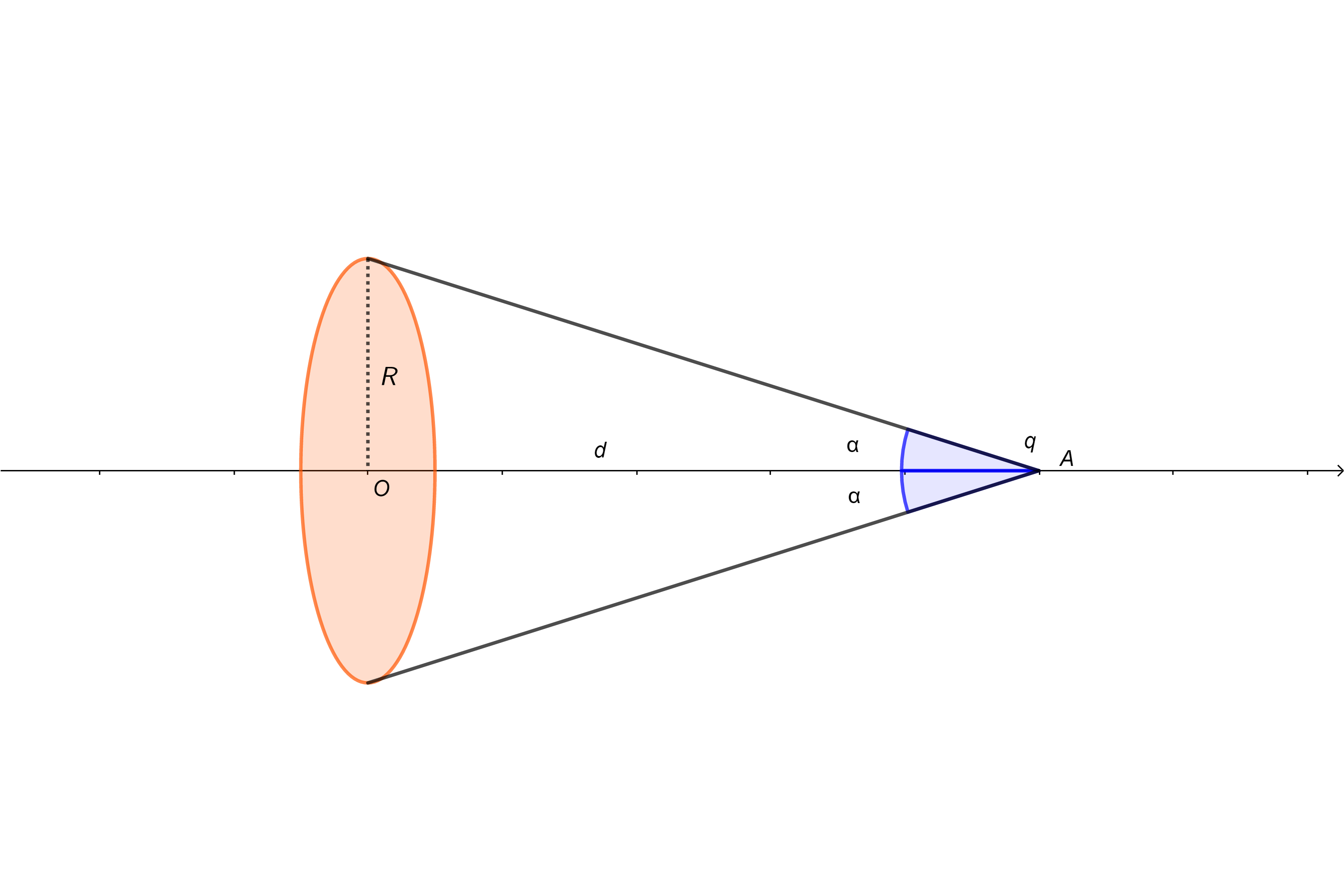
标准解法

解：设圆板边缘到点电荷的距离为r，以点电荷为球心，r为半径作一球面。该球面的面积为：

　　

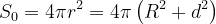
球冠面积(即截取的球面)为

　　

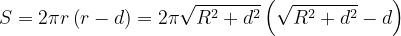
通过整个球面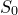的E通量为

　　

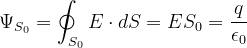
通过球冠面S的E通量，也就是通过圆形平面的E通量，为

　　

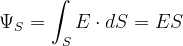
可得

　　

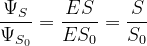
所以

　　

个人解法

解：由于

　　

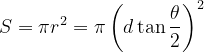
可得

　　

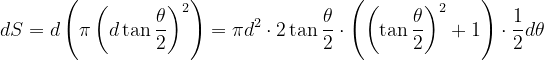
因此