从曲率半径的得出推导函数在某一点处的曲率公式

一、定义：

　　曲线的曲率：就是针对曲线上某个点的切线方向角对弧长的转动率，通过微分来定义，表明曲线偏离直线的程度。数学上表明曲线在某一点的弯曲程度的数值。

　　曲率半径：最接近该点处曲线的圆弧的半径，大小等于曲率的倒数。

二、求曲率半径思路：

　　将某点极短相邻区域内函数近似看作圆弧，通过圆弧长度/夹角可得出半径再令长度趋于0即可得到曲率半径的大小。

三、公式推导：

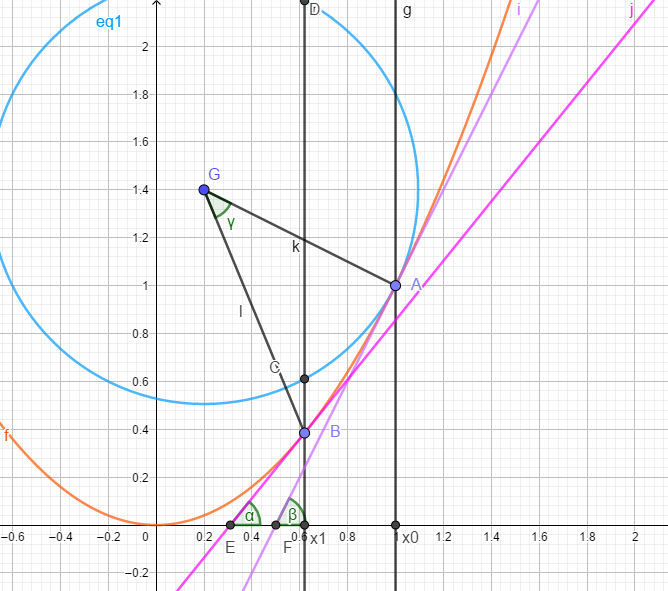
　　1.求弧长（近似代替曲率圆弧长）：

　　给定函数f(x)，要求其上一点(x0,f(x0))处的曲率半径，在x0邻域内取一点(x1,f(x1)),由弧长计算公式有：

　                                                                 　

即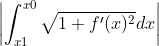                                                                   

 　　2.求夹角（近似代替曲率圆夹角）：

　　由于|x0-x1|非常小，曲率圆上的夹角近似于A,B两点到曲率圆圆心之间的夹角。夹角用两点处的切线的负倒数的反正切的差表示，

即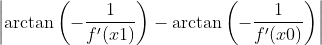                                                 

 

则曲率半径可表示为                    

                                                  

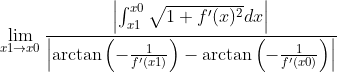
 　　3.求极限：

应用洛必达法则分子分母同时对x1求偏导数可得

 

                                                  

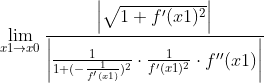
化简得

                                                              

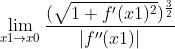
即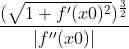                                                                 

因此，函数在任意一点处曲率圆的曲率半径为   

                                                                     

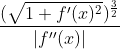
由于曲率半径与曲率大小互为倒数，则该点处曲率的值为

                                                                     

注意：

　　如果要求函数一点处曲率圆方程，求出曲率半径后还需判断函数在该点处的凸凹性来判断曲率圆圆心在函数的哪一侧，若

,则圆心在函数上侧，即圆心纵坐标大于该点的纵坐标，若 ，则圆心在函数下侧，即圆心纵坐标小于该点的纵坐标。