伯德图Bode Plot
伯德图Bode Plot
学习完B站
DR_CAN老师的动态系统的建模与分析：15、16后进行总结。
学习重点
理解伯德图
前情提要
-
系统的传递函数为\(G(S)\)
-
对于线性时不变系统（LTI，Linear Time Invariant）来说，当输入为\(M_i\sin{(\omega t+\phi_i)}\)时，系统
稳定时的输出为\(M_o\sin{(\omega t+\phi_o)}\)频率响应：\(M=\frac{M_o}{M_i}=|G(j\omega)|\)
幅角响应：\(\phi=\phi_o-\phi_i=\angle{G(j\omega)}\)
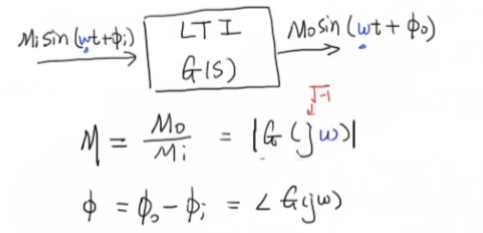
伯德图
伯德图是用来表示频率响应的图示方法，由荷兰裔美国工程师Hendrik Wade Bode创造。
伯德图由两部分组成，即两个子图构成：
-
振幅响应部分：
- 单位：分贝（dB, decibel<deci --代表-- 1/10， bel --代表-- Alexander Graham Bell,拥有电话专利的科学家>）
- 计算方法：\(20log_{10}M\),其中系数20的原由：分贝的原始定义用于描述电话/电报的信号损失，计算公式为\(10log_{10}\frac{P_M}{P_R}\)，其中\(P_M\)为
Measurement Power测量能量值，\(P_R\)为Reference Power参考能量值，实质上为能量的比值，取对数是为了缩小量程；一般来说，能量是振幅平方的函数\(P=f(M^2)\)(动能：\(E=\frac{1}{2}mv^2\),弹力势能：\(E=\frac{1}{2}kx^2\),电器功率：\(P=i^2R\))可以这样理解bode图的频率响应部分\(20log_{10}M=10log_{10}M^2\)。
-
幅角响应部分
- 单位：度\(^\circ\)
- 计算公式：该部分为幅角响应\(\phi\)
手绘技巧
手绘技巧并非掌握的重点，重点在于理解
手绘借助渐进线来完成，反映系统的频响趋势，具体计算时令输入频率\(\omega\)为不同特定值，进而得到的特殊值绘制渐进线。
性质
叠加原理
根据数学性质，对于混合的复杂系统，均可以拆分为基础的简单系统，其系统伯德图可以使用加法进行计算。
常见传递函数伯德图
举例说明
如下传递函数，可因式分解为由基础传递函数构成的系统，分别画出各部分的bode图，再将其相加即可
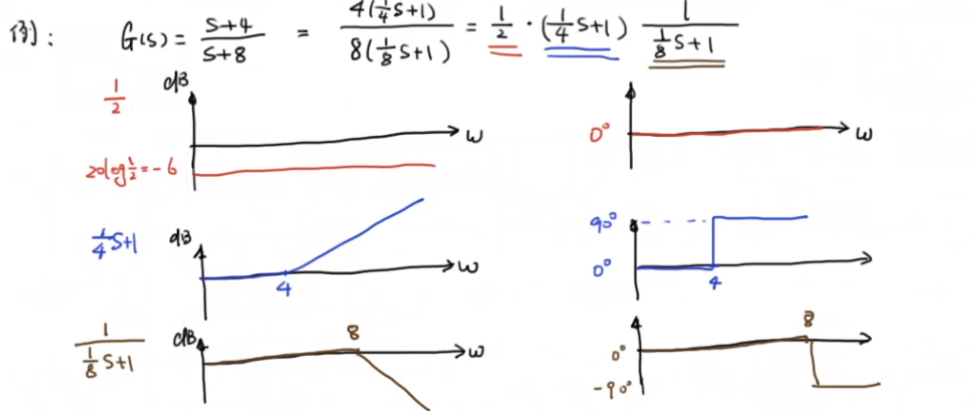
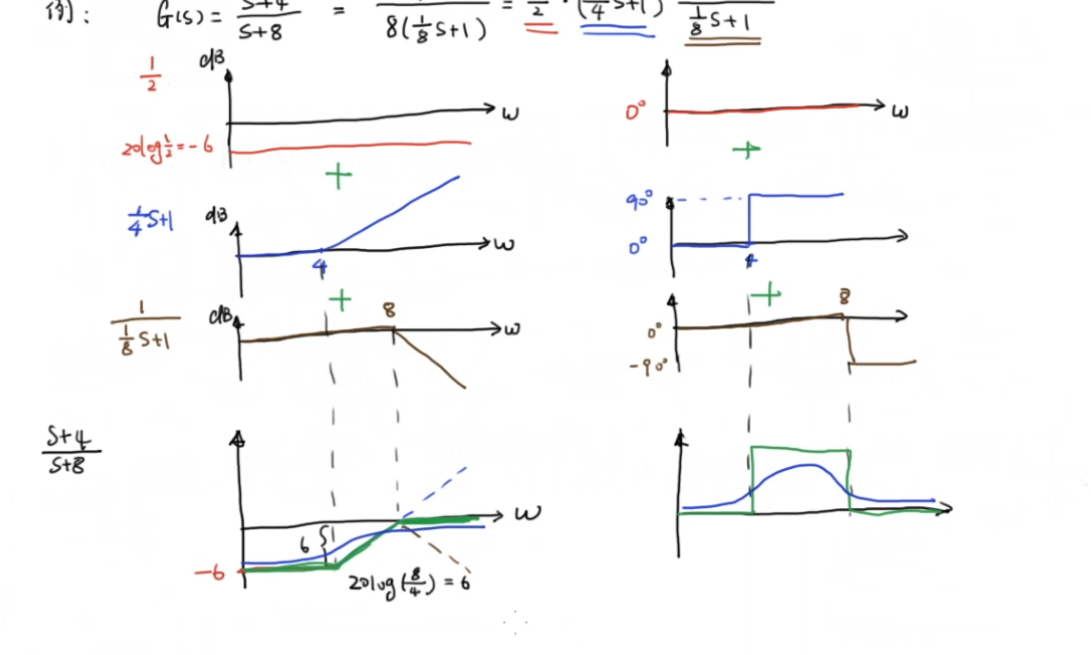
原课程资料：
- 【【动态系统的建模与分析】15_伯德图，为什么是20logM？分贝又是什么？_Bode Plot_Part1】
- 【【动态系统的建模与分析】16_伯德图_手绘技巧与应用_Bode Plot_Part2】
