手写数字识别[paddle框架]:3.损失函数
[手写数字识别]之损失函数
概述
上一节我们尝试通过更复杂的模型(经典的全连接神经网络和卷积神经网络),提升手写数字识别模型训练的准确性。本节我们继续将“横纵式”教学法从横向展开,如 图1 所示,探讨损失函数的优化对模型训练效果的影响。
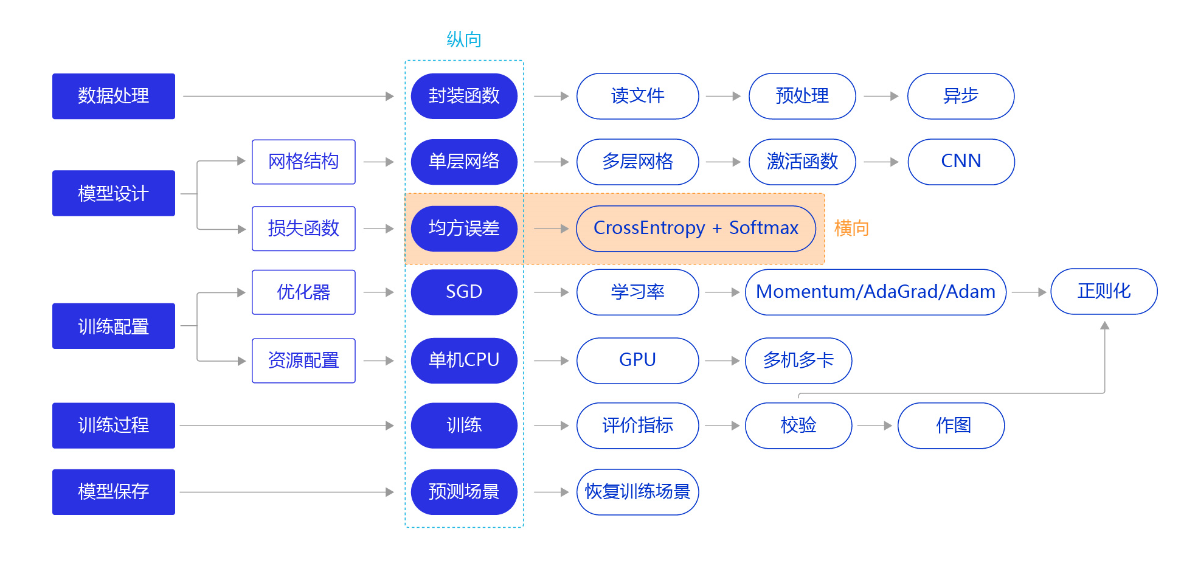
图1:“横纵式”教学法 — 损失函数优化
- 先根据输入数据正向计算预测输出。
- 再根据预测值和真实值计算损失。
- 最后根据损失反向传播梯度并更新参数。
分类任务的损失函数
在之前的方案中,我们复用了房价预测模型的损失函数-均方误差。从预测效果来看,虽然损失不断下降,模型的预测值逐渐逼近真实值,但模型的最终效果不够理想。究其根本,不同的深度学习任务需要有各自适宜的损失函数(类似强化学习需要设置不同的奖惩函数)。我们以房价预测和手写数字识别两个任务为例,详细剖析其中的缘由如下:
- 房价预测是回归任务,而手写数字识别是分类任务,使用均方误差作为分类任务的损失函数存在逻辑和效果上的缺欠。
- 房价可以是大于0的任何浮点数,而手写数字识别的输出只可能是0-9之间的10个整数,相当于一种标签。
- 在房价预测的案例中,由于房价本身是一个连续的实数值,因此以模型输出的数值和真实房价差距作为损失函数(loss)是符合道理的。但对于分类问题,真实结果是分类标签,而模型输出是实数值,导致以两者相减作为损失不具备物理含义。
即,均方误差不适用于分类任务
那么,什么是分类任务的合理输出呢?分类任务本质上是“某种特征组合下的分类概率”,下面以一个简单案例说明,如 图2 所示。

图2:观测数据和背后规律之间的关系
Softmax函数
如果模型能输出10个标签的概率,对应真实标签的概率输出尽可能接近100%,而其他标签的概率输出尽可能接近0%,且所有输出概率之和为1。这是一种更合理的假设!与此对应,真实的标签值可以转变成一个10维度的one-hot向量,在对应数字的位置上为1,其余位置为0,比如标签“6”可以转变成[0,0,0,0,0,1,0,0,0,0]。
为了实现上述思路,需要引入Softmax函数,它可以将原始输出转变成对应标签的概率,公式如下,其中是标签类别个数。
从公式的形式可见,每个输出的范围均在0~1之间,且所有输出之和等于1,这是这种变换后可被解释成概率的基本前提。对应到代码上,我们需要在网络定义部分修改输出层:self.fc = Linear(input_dim=10, output_dim=1, act='softmax'),即是对全连接层的输出加一个softmax运算。
图3 是一个三个标签的分类模型(三分类)使用的softmax输出层,从中可见原始输出的三个数字3、1、-3,经过softmax层后转变成加和为1的三个概率值0.88、0.12、0。
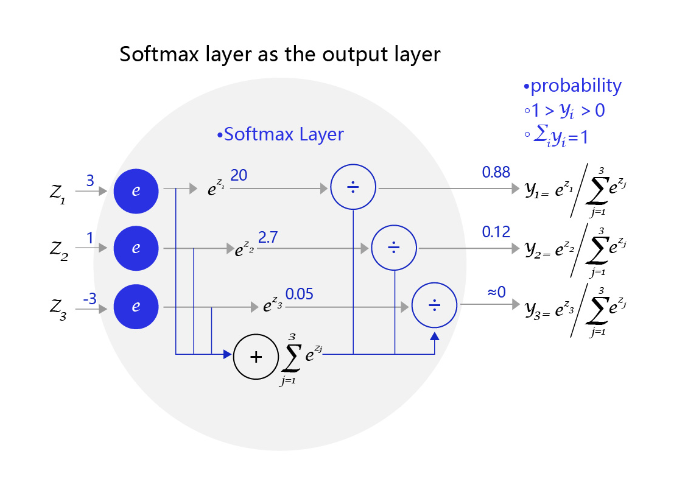
图3:网络输出层改为softmax函数
对于二分类问题,使用两个输出接入softmax作为输出层,等价于使用单一输出接入Sigmoid函数。如 图4 所示,利用两个标签的输出概率之和为1的条件,softmax输出0.6和0.4两个标签概率,从数学上等价于输出一个标签的概率0.6。
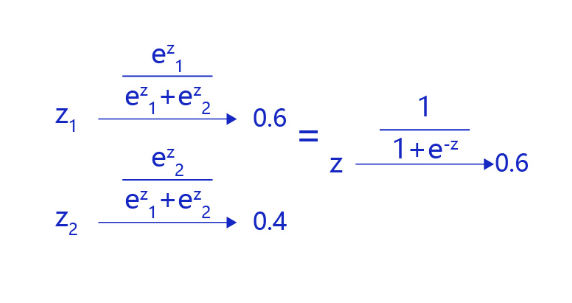
图4:对于二分类问题,等价于单一输出接入Sigmoid函数
图5 是肿瘤大小和肿瘤性质的数据图。从图中可发现,往往尺寸越大的肿瘤几乎全部是恶性,尺寸极小的肿瘤几乎全部是良性。只有在中间区域,肿瘤的恶性概率会从0逐渐到1(绿色区域),这种数据的分布是符合多数现实问题的规律。如果我们直接线性拟合,相当于红色的直线,会发现直线的纵轴0-1的区域会拉的很长,而我们期望拟合曲线0-1的区域与真实的分类边界区域重合。那么,观察下Sigmoid的曲线趋势可以满足我们对个问题的一切期望,它的概率变化会集中在一个边界区域,有助于模型提升边界区域的分辨率。
即,Sigmoid函数在上述情况下,有助于模型提升边界区域的分辨率
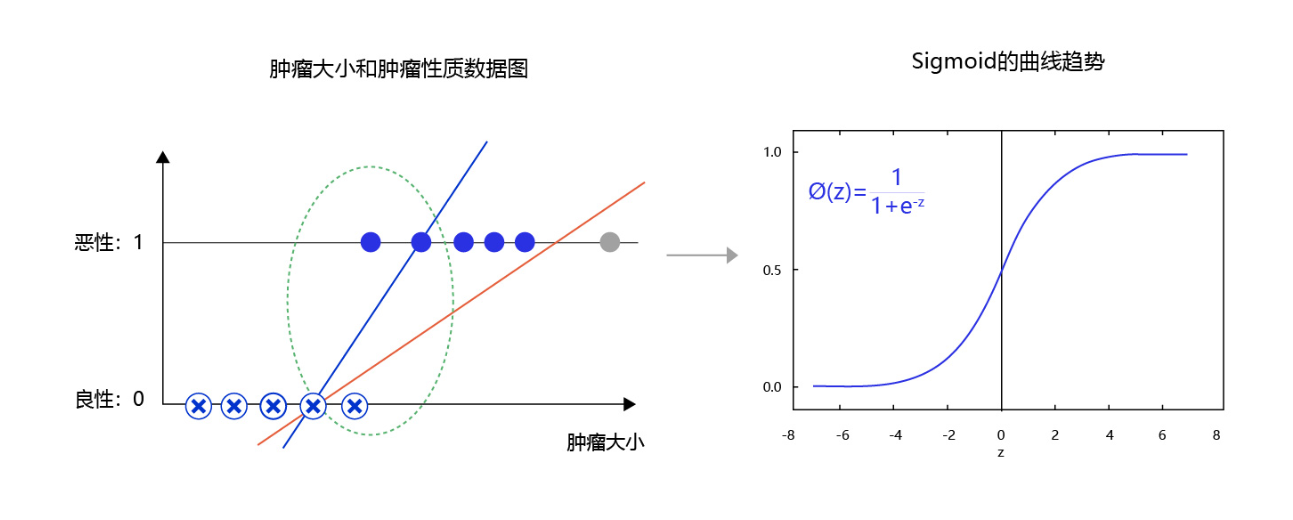
图5:使用sigmoid拟合输出可提高分类模型对边界的分辨率
图6:热水器水温控制
在模型输出为分类标签的概率时,直接以标签和概率做比较也不够合理,人们更习惯使用交叉熵误差作为分类问题的损失衡量。
交叉熵损失函数的设计是基于最大似然思想:最大概率得到观察结果的假设是真的。如何理解呢?举个例子来说,如 图7 所示。有两个外形相同的盒子,甲盒中有99个白球,1个黑球;乙盒中有99个黑球,1个白球。一次试验取出了一个黑球,请问这个球应该是从哪个盒子中取出的?
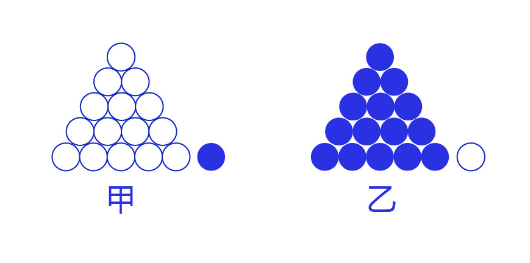
图7:体会最大似然的思想
依据贝叶斯公式,某二分类模型“生成”个训练样本的概率:
说明:
对于二分类问题,模型为,为Sigmoid函数。当=1,概率为;当=0,概率为。
经过公式推导,使得上述概率最大等价于最小化交叉熵,得到交叉熵的损失函数。交叉熵的公式如下:
其中,表示以为底数的自然对数。代表模型输出,代表各个标签。中只有正确解的标签为1,其余均为0(one-hot表示)。
因此,交叉熵只计算对应着“正确解”标签的输出的自然对数。比如,假设正确标签的索引是“2”,与之对应的神经网络的输出是0.6,则交叉熵误差是;若“2”对应的输出是0.1,则交叉熵误差为。由此可见,交叉熵误差的值是由正确标签所对应的输出结果决定的。
自然对数的函数曲线可由如下代码实现。
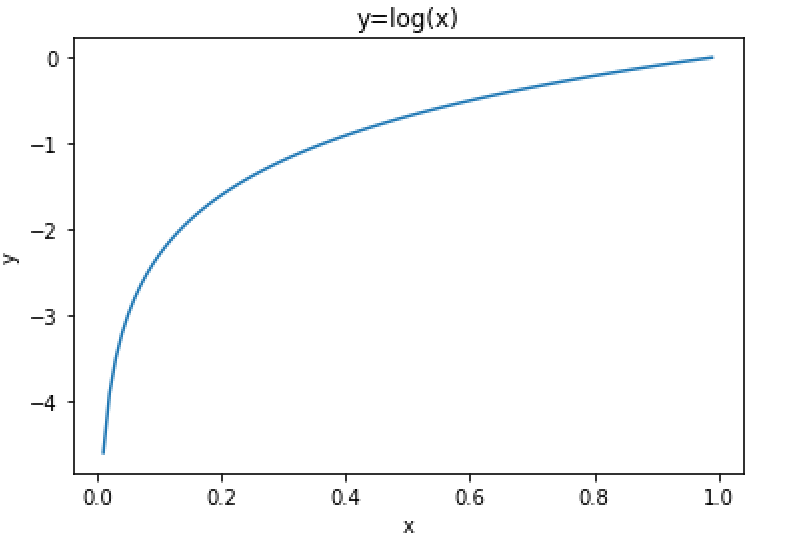
图8:自然对数曲线
交叉熵的代码实现
在手写数字识别任务中,仅改动三行代码,就可以将在现有模型的损失函数替换成交叉熵(cross_entropy)。
-
在读取数据部分,将标签的类型设置成int,体现它是一个标签而不是实数值(飞桨框架默认将标签处理成int64)。
在数据处理部分,需要修改标签变量Label的格式,代码如下所示。 - 从:label = np.reshape(labels[i], [1]).astype('float32') - 到:label = np.reshape(labels[i], [1]).astype('int64') -
在网络定义部分,将输出层改成“输出十个标签的概率”的模式。
在网络定义部分,需要修改输出层结构,代码如下所示。 - 从:self.fc = Linear(input_dim=980, output_dim=1, act=None) - 到:self.fc = Linear(input_dim=980, output_dim=10, act='softmax') -
在训练过程部分,将损失函数从均方误差换成交叉熵。
修改计算损失的函数,从均方误差(常用于回归问题)到交叉熵误差(常用于分类问题),代码如下所示。 - 从:loss = fluid.layers.square_error_cost(predict, label) - 到:loss = fluid.layers.cross_entropy(predict, label)
代码实现
1.数据读取:
#修改标签数据的格式,从float32到int64
import os
import random
import paddle
import paddle.fluid as fluid
from paddle.fluid.dygraph.nn import Conv2D, Pool2D, Linear
import numpy as np
from PIL import Image
import gzip
import json
# 定义数据集读取器
def load_data(mode='train'):
# 数据文件
datafile = './work/mnist.json.gz'
print('loading mnist dataset from {} ......'.format(datafile))
data = json.load(gzip.open(datafile))
train_set, val_set, eval_set = data
# 数据集相关参数,图片高度IMG_ROWS, 图片宽度IMG_COLS
IMG_ROWS = 28
IMG_COLS = 28
if mode == 'train':
imgs = train_set[0]
labels = train_set[1]
elif mode == 'valid':
imgs = val_set[0]
labels = val_set[1]
elif mode == 'eval':
imgs = eval_set[0]
labels = eval_set[1]
imgs_length = len(imgs)
assert len(imgs) == len(labels), \
"length of train_imgs({}) should be the same as train_labels({})".format(
len(imgs), len(labels))
index_list = list(range(imgs_length))
# 读入数据时用到的batchsize
BATCHSIZE = 100
# 定义数据生成器
def data_generator():
if mode == 'train':
random.shuffle(index_list)
imgs_list = []
labels_list = []
for i in index_list:
img = np.reshape(imgs[i], [1, IMG_ROWS, IMG_COLS]).astype('float32')
#---------------------------------------------------------------
# 将标签类型数据设置为int
label = np.reshape(labels[i], [1]).astype('int64')
#---------------------------------------------------------------
imgs_list.append(img)
labels_list.append(label)
if len(imgs_list) == BATCHSIZE:
yield np.array(imgs_list), np.array(labels_list)
imgs_list = []
labels_list = []
# 如果剩余数据的数目小于BATCHSIZE,
# 则剩余数据一起构成一个大小为len(imgs_list)的mini-batch
if len(imgs_list) > 0:
yield np.array(imgs_list), np.array(labels_list)
return data_generator
2.网络结构
# 定义模型结构
class MNIST(fluid.dygraph.Layer):
def __init__(self):
super(MNIST, self).__init__()
# 定义一个卷积层,使用relu激活函数
self.conv1 = Conv2D(num_channels=1, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')
# 定义一个池化层,池化核为2,步长为2,使用最大池化方式
self.pool1 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
# 定义一个卷积层,使用relu激活函数
self.conv2 = Conv2D(num_channels=20, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')
# 定义一个池化层,池化核为2,步长为2,使用最大池化方式
self.pool2 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
#---------------------------------------------------------------
# 定义一个全连接层,输出节点数为10
# softmax函数输出某样本属于不同类别(标签)的概率
self.fc = Linear(input_dim=980, output_dim=10, act='softmax')
#---------------------------------------------------------------
# 定义网络的前向计算过程
def forward(self, inputs):
x = self.conv1(inputs)
x = self.pool1(x)
x = self.conv2(x)
x = self.pool2(x)
x = fluid.layers.reshape(x, [x.shape[0], 980])
x = self.fc(x)
return x
3.训练配置
#仅修改计算损失的函数,从均方误差(常用于回归问题)到交叉熵误差(常用于分类问题)
with fluid.dygraph.guard():
model = MNIST()
model.train()
#调用加载数据的函数
train_loader = load_data('train')
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
EPOCH_NUM = 20
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据,变得更加简洁
image_data, label_data = data
image = fluid.dygraph.to_variable(image_data)
label = fluid.dygraph.to_variable(label_data)
#前向计算的过程
predict = model(image)
#计算损失,使用交叉熵损失函数,取一个批次样本损失的平均值
loss = fluid.layers.cross_entropy(predict, label)
avg_loss = fluid.layers.mean(loss)
#每训练了200批次的数据,打印下当前Loss的情况
if batch_id % 200 == 0:
print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
#后向传播,更新参数的过程
avg_loss.backward()
optimizer.minimize(avg_loss)
model.clear_gradients()
#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')
训练输出:
...
...
epoch: 16, batch: 0, loss is: [0.04718658]
epoch: 16, batch: 200, loss is: [0.05045929]
epoch: 16, batch: 400, loss is: [0.03693192]
epoch: 17, batch: 0, loss is: [0.08631954]
epoch: 17, batch: 200, loss is: [0.01391332]
epoch: 17, batch: 400, loss is: [0.06397887]
epoch: 18, batch: 0, loss is: [0.03962973]
epoch: 18, batch: 200, loss is: [0.01085799]
epoch: 18, batch: 400, loss is: [0.05781446]
epoch: 19, batch: 0, loss is: [0.06044349]
epoch: 19, batch: 200, loss is: [0.01827444]
epoch: 19, batch: 400, loss is: [0.05743753]
虽然上述训练过程的损失明显比使用均方误差算法要小,但因为损失函数量纲的变化,我们无法从比较两个不同的Loss得出谁更加优秀。怎么解决这个问题呢?我们可以回归到问题的本质,谁的分类准确率更高来判断。在后面介绍完计算准确率和作图的内容后,读者可以自行测试采用不同损失函数下,模型准确率的高低。
至此,大家阅读论文中常见的一些分类任务模型图就清晰明了,如全连接神经网络、卷积神经网络,在模型的最后阶段,都是使用Softmax进行处理。
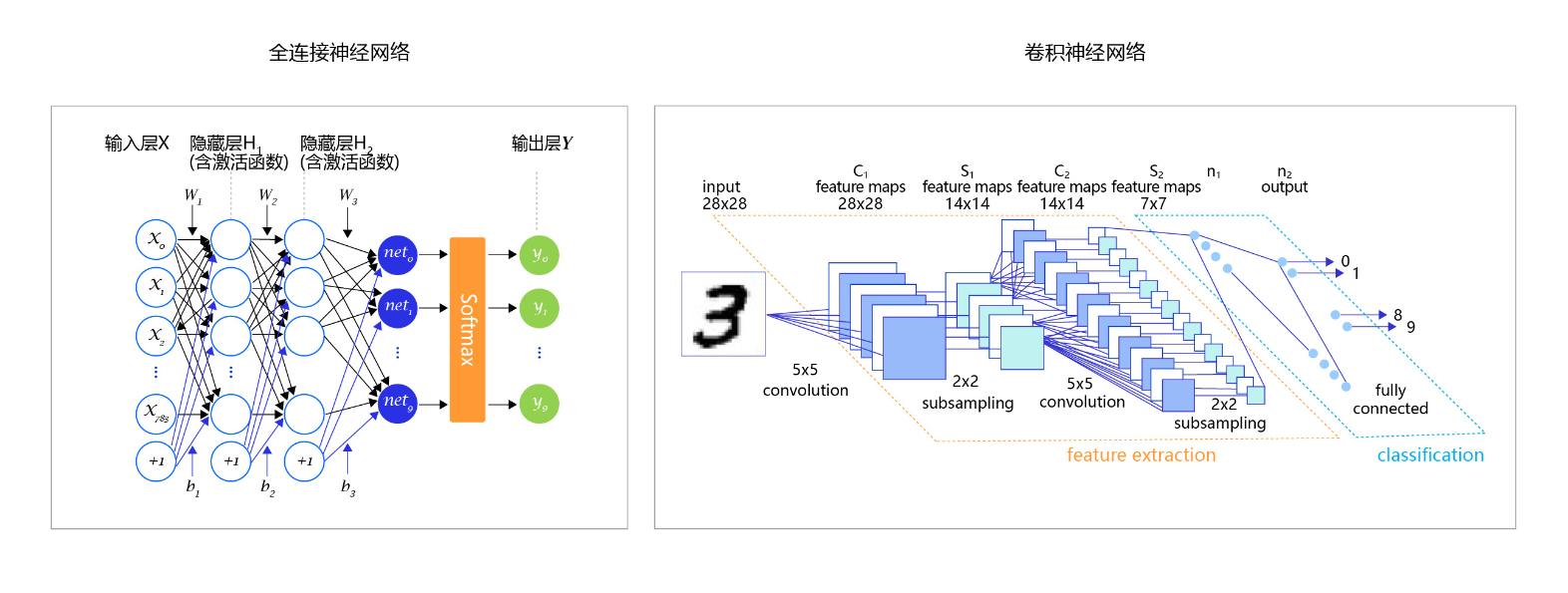
图8:常见的分类任务模型图
4.模型预测
封装评估模型函数
# 封装评估模型函数
def eval_model(model_class, model_file, data):
# 计算准确率
def calculate_ACC(pres, labels):
assert pres.shape == labels.shape,'pres.shape:{} != labels.shape:{} is required when calculat ACC'.format(pres.shape, labels.shape)
count = 0
for i in pres.astype('int32') == labels:
if i:
count += 1
acc = count / len(labels)
return acc
# 定义飞浆动态图工作环境
imgs, labels = data
with fluid.dygraph.guard():
model = model_class()
model_dict, _ = fluid.load_dygraph(model_file)
# 加载模型参数
model.load_dict(model_dict)
# 设置模型工作模式,灌入测试数据
model.eval()
results = model(fluid.dygraph.to_variable(imgs))
# 对于softmax输出单独处理
results = np.argmax(results.numpy(), axis = 1).reshape(-1,1)
# print('predict results shape:{}'.format(results.numpy().shape))
model_acc = calculate_ACC(results, labels)
# print('Acc of model is:{}%'.format(model_acc*100))
return model_acc
预测配置
eval_loader = load_data('eval')
acc_list = []
for id, data in enumerate(eval_loader()):
acc = eval_model(MNIST, 'mnist', data) * 100
print('id:{},acc:{}'.format(id, acc))
# print('eval images shape is:{}\neval labels shape is:{}'.format(data[0].shape, data[1].shape))
acc_list.append(acc)
# 计算训练20个epoch后模型的预测准确率
print('Acc of model is:{}%'.format(np.mean(acc_list)))
输出:
...
...
id:79,acc:99.0
id:80,acc:99.0
id:81,acc:100.0
id:82,acc:100.0
id:83,acc:99.0
id:84,acc:99.0
id:85,acc:100.0
id:86,acc:100.0
id:87,acc:100.0
id:88,acc:100.0
id:89,acc:100.0
id:90,acc:97.0
id:91,acc:100.0
id:92,acc:100.0
id:93,acc:100.0
id:94,acc:100.0
id:95,acc:99.0
id:96,acc:94.0
id:97,acc:97.0
id:98,acc:94.0
id:99,acc:99.0
Acc of model is:98.36%
5.结论
比较上一节使用均方误差作为损失函数的模型(准确率36.7%),明显可知使用交叉熵损失函数的模型准确率更高,准确率为98.4%






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!