CF1715F Crop Squares 题解
CF1715F Crop Squares solution
有一个 \(n \times m\) 的长方形,四个角的坐标分别为 $ (0, 0) $ , $ (0, m) $ , $ (n, 0) $ , $ (n, m) $。在长方形里面有一个 \(1 \times 1\) 的正方形,边平行于长方形边界。你需要询问出这个正方形的位置。每次询问,每次你可以询问正方形与你提问的多边形的相交面积。你最多可以进行 \(5\) 次询问。
额外信息:答案要求精度为 \(10^{-6}\),而询问和回复的精度为 \(10^{-15}\)。
题解给出的做法非常巧妙,但是数学巨佬 majorGYY 给出了另一种实用的方法。
一个通用的思路是分别询问出纵坐标和横坐标。
如图,黑色框为总的范围,蓝色矩形的宽度互不相等,两个蓝色矩形之间的间隔为 \(1.0\),红色为要求的正方形。
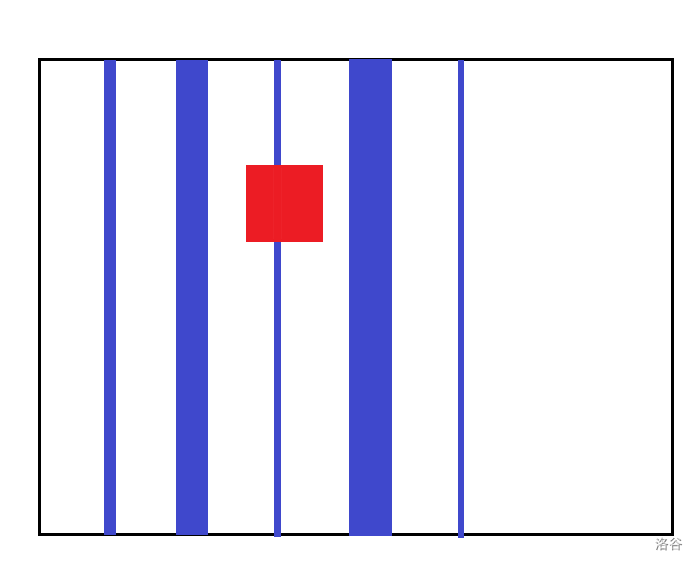
可以发现一个正方形恰好只会覆盖一个蓝色矩形,同时如果是覆盖了整个矩形的宽(即矩形较短的一边)的话,还能发现覆盖的面积的值就是矩形的宽。又因为每个矩形的宽互不相同,那么可以得到正方形的大致位置。
为了保证正方形完全覆盖矩形的宽,我们可以给矩形的宽定一个很小的值,这样没有被完全覆盖的概率就很小了。
确定了正方形的大致位置后,我们需要第二次询问来定位正方形一个坐标的具体值,如图:
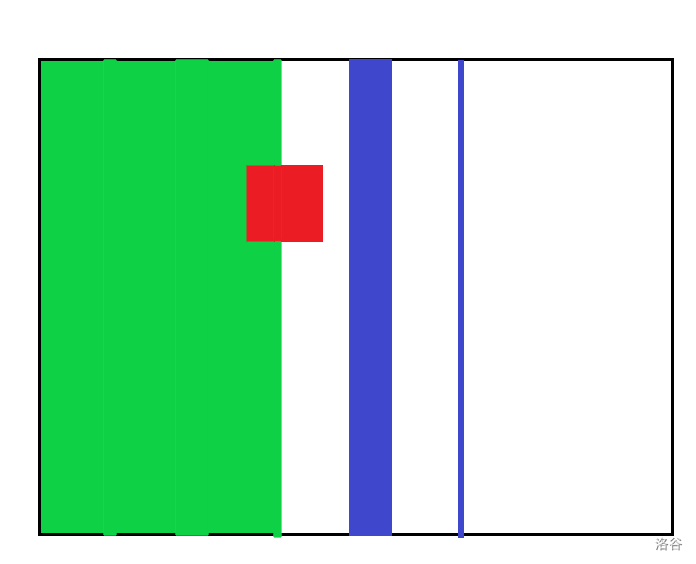
我们查询上次覆盖的矩形到坐标轴所形成的矩形与正方形的交,可以得出面积交即为上次覆盖矩形的坐标减去这个正方形的坐标。自此就得到了矩形的一个精准坐标,花费 \(2\) 次询问,然后另一个坐标用同样的方法做就好了,一共 \(4\) 次询问。
那么这时就会有同学说了,第一次查询时候不是要查询 \(n\) 个矩形吗,怎么就能一次搞定呢?其实也好办,题目并不要求一定是凸多边形,我们只需要给这 \(n\) 个矩形一个公共的矩形作为底即可,这个作为底的矩形宽度还要远小于其他矩形的宽。
实现
我是给作为查询的蓝色矩形在 \([10^{-12},10^{-10}]\) 的取值范围,作为底的矩形的宽度取到 \(10^{-14}\)。然后没有调参什么的就一遍过了。
其他实现见代码,不涉及斜率什么的计算几何知识,应该不是很难。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <random>
#include <chrono>
#include <iomanip>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef long double ld;
const ld EPS=1e-14;
mt19937 gen(chrono::system_clock::now().time_since_epoch().count());
uniform_real_distribution<ld>lent(1e-10,1e-12);
const int N=103;
int n,m;
ld hei[N],ansx,ansy,area,pos[N];
int main(){
cin>>n>>m;
for(int i=1;i<=n;++i)hei[i]=lent(gen);
sort(hei+1,hei+1+n);
ld x=0;
cout<<"? "<<4*n+2<<endl;
cout<<fixed<<setprecision(15)<<x<<' '<<0.0<<endl<<flush;
for(int i=1;i<=n;++i){
cout<<fixed<<setprecision(15)<<x<<' '<<EPS<<endl<<flush;
cout<<fixed<<setprecision(15)<<x<<' '<<(ld)m<<endl<<flush;
x+=hei[i];
pos[i]=x;
cout<<fixed<<setprecision(15)<<x<<' '<<(ld)m<<endl<<flush;
cout<<fixed<<setprecision(15)<<x<<' '<<EPS<<endl<<flush;
if(i!=n)x+=1.0;
}
cout<<fixed<<setprecision(15)<<x<<' '<<0.0<<endl<<flush;
cin>>area;
int loc=lower_bound(hei+1,hei+1+n,area)-hei;
if(fabs(area-hei[loc])>fabs(area-hei[loc-1]))loc=loc-1;
cout<<"? "<<4<<endl<<flush;
cout<<0<<' '<<0<<endl<<flush;
cout<<0<<' '<<m<<endl<<flush;
cout<<fixed<<setprecision(15)<<pos[loc]<<' '<<(ld)m<<endl<<flush;
cout<<fixed<<setprecision(15)<<pos[loc]<<' '<<0.0<<endl<<flush;
cin>>area;
ansx=pos[loc]-area;
for(int i=1;i<=m;++i)hei[i]=lent(gen);
sort(hei+1,hei+1+m);
x=0;
cout<<"? "<<4*m+2<<endl;
cout<<fixed<<setprecision(15)<<0.0<<' '<<x<<endl<<flush;
for(int i=1;i<=m;++i){
cout<<fixed<<setprecision(15)<<EPS<<' '<<x<<endl<<flush;
cout<<fixed<<setprecision(15)<<(ld)n<<' '<<x<<endl<<flush;
x+=hei[i];
pos[i]=x;
cout<<fixed<<setprecision(15)<<(ld)n<<' '<<x<<endl<<flush;
cout<<fixed<<setprecision(15)<<EPS<<' '<<x<<endl<<flush;
if(i!=m)x+=1.0;
}
cout<<fixed<<setprecision(15)<<0.0<<' '<<x<<endl<<flush;
cin>>area;
loc=lower_bound(hei+1,hei+1+m,area)-hei;
if(fabs(area-hei[loc])>fabs(area-hei[loc-1]))loc=loc-1;
cout<<"? "<<4<<endl<<flush;
cout<<0<<' '<<0<<endl<<flush;
cout<<n<<' '<<0<<endl<<flush;
cout<<fixed<<setprecision(15)<<(ld)n<<' '<<pos[loc]<<endl<<flush;
cout<<fixed<<setprecision(15)<<0.0<<' '<<pos[loc]<<endl<<flush;
cin>>area;
ansy=pos[loc]-area;
cout<<"! "<<fixed<<setprecision(15)<<ansx<<' '<<ansy<<endl<<flush;
return 0;
}
后记
再次感谢 majorGYY 提供的全新思路(如有雷同,纯属巧合)。此外这个做法对精度以及一些细节的要求比较严格,我实现的时候肯定也有地方处理不当,相信是可以被 hack 的,还请大家多多指正。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号