Z 函数(扩展KMP)
Z
其实我也不知道是 Z-algorithm 还是 function Z。
问题描述
\(\text{extraKMP}\) 经典问题:给定字符串 \(S,T\),\(length_s=n,length_t=m\), 请输出 \(S\) 的每一个后缀与 \(T\) 的最长公共前缀。
变量定义
\(extend_{i,n}\) 表示串 \(S_{i,n}\) 与串 \(T\) 的最长公共前缀长度(即题目所求)
\(next_i\) 表示 \(T_{i,m}\) 与\(T\)的最长公共前缀长度(是不是和 \(extend\) 很像)
题解
一般情况:
此时\(extend_{1...k}\)已经算好,设在以前的匹配过程中S串最远的距离为 \(p\),故 \(p=\max(i+extend_i-1)\) ,其中 \(1\leq i\leq k\)
令在之前\(i...k\)的匹配中匹配到 \(p\) 的位置为 \(p_0\)
根据匹配的定义有 \(S_{p0,p}=T_{1,p-p_0+1}\)
为了方便讲解,定义 \(a=k-p_0+1,b=k-p_0+2\)(说白了就是当\(T_1\) 位置与 \(S_{p_0}\)位置对齐时候,\(T_a\) 与 \(S_k\) 对齐,而 \(b\) 是 \(a\) 的下一位)。再令 \(l=next_b\)。
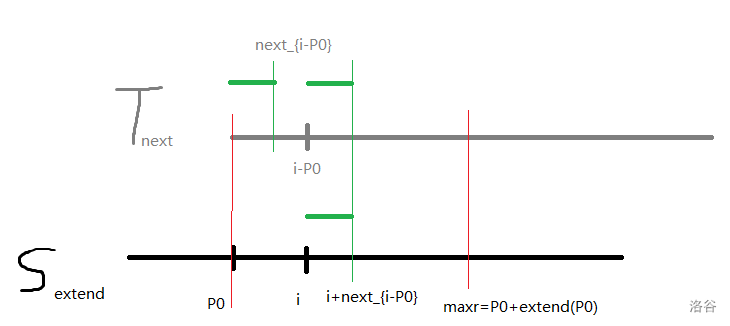
(原创图,完美阐述了情况一,情况二也可以参考该图很快得出,复习的话看这张图就懂了,不用看下面繁琐的说明。图中两红线中间的段和绿色的段中字符是相等的,灰色和黑色分别代表 \(T\) 和 \(S\) 的下标。)
有两种情况讨论
\(1^{\circ}\) \(k+l<p\)
根据 \(next\) 的定义 \(T_{1,l}=T_{b,b+l-1}\) 且 \(T_{l+1}\neq T_{b+l}\)
又 \(S_{p0,p}=T_{1,p-p_0+1}\)
∴ \(S_{k+1,k+l}=T_{1,l}\) 即 \(extend_{k+1}=l\)
if(i+next[i-p0]<extend[p0]+p0)//i相当于k+1,即现在匹配的位置
extend[i]=next[i-p0];
//因为从0开始记录字符串,所以本来应该在小于号左侧-1,但现在不用
\(2^{\circ}\) \(p\leq k+l\)
定义 \(k+l\) 到 \(p\) 的距离为 \(x\) ,即 \(x=k+l-p\)
由 \(next\) 定义,\(T_{1,l}=T_{b,b+l-1}\),而此时 \(k-p_0+2=b<l\),可以得到 \(T_{1,l-x+1}=T_{b,b+l-x}\)
又 \(S_{p0,p}=T_{1,p-p_0+1}\)
所以 \(T_{1,l-x+1}=T_{b,b+l-x}=S_{k+1,p}\)
这就是现在已经匹配成功的长度
所以接下来就像 KMP 一样从 \(S_{p+1}\) 和 \(T_{l-x+2}\) 开始暴力扩展
else{
int now=extend[p0]+p0-i;//现在开始暴力扩展的长度
now=max(now,0);//防止i>p
while(t[now]==s[i+now]&&now<(int)t.size()&&now+i<(int)s.size)
++now;
extend[i]=now;
p0=i;//更新位置
}
求next
我们发现 \(next\) 的定义和 \(extend\) 的定义十分相似,所不同的是 \(next\) 就是 \(T\) 自己匹配自己。要注意的一点是:求 \(next\) 时我们要从第 \(2\) 位(也就是代码中的第 \(1\) 位)开始暴力,这样能防止求 \(next\) 时引用自己 \(next\) 值的情况。
CODE
P5410 【模板】扩展 KMP(Z 函数)
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
const int N=2e7+7;
char s[N],t[N];int lens,lent;//字符串相关变量
int next[N],extend[N];//扩展KMP相关变量
void getnext(){//t自己匹配自己
next[0]=lent;//next[0]就是t本身的长度
int now=0,p0=1;
while(t[now]==t[1+now]&&now+1<lent)++now;//从1开始暴力
next[1]=now;
for(int i=2;i<lent;++i){
if(i+next[i-p0]<next[p0]+p0)next[i]=next[i-p0];
else{
now=max(next[p0]+p0-i,0);
while(t[now]==t[i+now]&&i+now<lent)++now;
next[i]=now;p0=i;
}
}
}
void extraKMP(){
getnext();//先获取一遍next数组
int now=0,p0=0;
while(s[now]==t[now]&&now<min(lens,lent))++now;//先暴力扩展一遍
extend[0]=now;
for(int i=1;i<lens;++i){
if(i+next[i-p0]<extend[p0]+p0)extend[i]=next[i-p0];
else{
now=max(extend[p0]+p0-i,0);
while(t[now]==s[i+now]&&i+now<lens&&now<lent)++now;
extend[i]=now;p0=i;
}
}
}
int main(){
scanf("%s%s",s,t);lens=strlen(s),lent=strlen(t);
extraKMP();
ll ans1=0,ans2=0;//题目要求输出的答案
for(int i=0;i<lent;++i)ans1^=1ll*(i+1)*(next[i]+1);
for(int i=0;i<lens;++i)ans2^=1ll*(i+1)*(extend[i]+1);
printf("%lld\n%lld\n",ans1,ans2);
return 0;
}// 6.33s / 191.63MB / 1.14KB C++
写法改进
鉴于大多数字符串从 \(1\) 开始存储,而且两个函数要写20多行并不美观,故采用核心原理相同但是大量缩短篇幅的写法。
其中 \(l\) 代表 \(p_0\),\(r\) 代表 \(p\)。许多加一减一从长度的角度理解即可。
int n,m,tot,nxt[N],ext[N];
char s[N],t[N];
int main(){
scanf("%s%s",s+1,t+1);//更现代化的写法(不是)
n=strlen(s+1),m=strlen(t+1);
nxt[1]=m;
for(int i=2,l=0,r=0;i<=m;++i){
if(i<=r)nxt[i]=min(r-i+1,nxt[i-l+1]);
else nxt[i]=0;
while(i+nxt[i]<=m&&t[1+nxt[i]]==t[i+nxt[i]])++nxt[i];
if(r<i+nxt[i]-1)l=i,r=i+nxt[i]-1;
}
for(int i=1,l=0,r=0;i<=n;++i){
if(i<=r)ext[i]=min(r-i+1,nxt[i-l+1]);
else ext[i]=0;
while(1+ext[i]<=m&&i+ext[i]<=n&&t[1+ext[i]]==s[i+ext[i]])++ext[i];
if(r<i+ext[i]-1)l=i,r=i+ext[i]-1;
}
ll ans1=0,ans2=0;
for(int i=1;i<=n;++i)ans1^=(ll)i*(ext[i]+1);
for(int i=1;i<=m;++i)ans2^=(ll)i*(nxt[i]+1);
printf("%lld\n%lld\n",ans2,ans1);
return 0;
}// 3.42s / 191.50MB / 810B C++14 (GCC 9) O2
例题
exKMP 的应用比较局限,相关的题目也较少,许多它能做的更简单的字符串算法也能做。
LG7114 [NOIP2020] 字符串匹配
我们可以定义 \(AB\) 表示两个字符串 \(A\),\(B\) 相连接,例如 \(A = \texttt{aab}\),\(B = \texttt{ab}\),则 \(AB = \texttt{aabab}\)。
并递归地定义 \(A^1=A\),\(A^n = A^{n - 1} A\)(\(n \ge 2\) 且为正整数)。例如 \(A = \texttt{abb}\),则 \(A^3=\texttt{abbabbabb}\)。
则小 C 的习题是求 \(S = {(AB)}^iC\) 的方案数,其中 \(F(A) \le F(C)\),\(F(S)\) 表示字符串 \(S\) 中出现奇数次的字符的数量。两种方案不同当且仅当拆分出的 \(A\)、\(B\)、\(C\) 中有至少一个字符串不同。
求解循环节长度
因为 \(S\) 可以表示成形如 \((AB)^kC\) 的形式,那么 \((AB)\) 毫无疑问是 \(S\) 去掉末尾 \(C\) 串后的循环节。
假设循环节的长度为 \(i\),容易发现为了满足题目限制 \(2\leq i\leq n-1\)。当循环长度为 \(i\) 时,他的最少循环次数为 \(1\),现在我们需要求最长的循环次数 \(k\) 。然后 \(C\) 串的最短取值长度就是 \(|S|-k\times i\)。
这个问题可以使用 \(\text{Z-algo}\) 轻松解决。
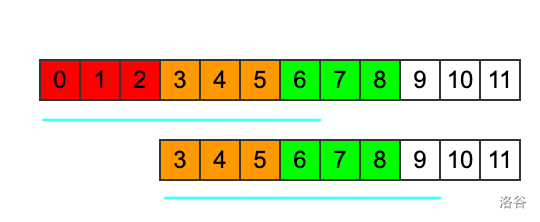
假设 \(next_i=x\),那么意味着 \(S_{i,|S|-1}\) 与 \(S\) 的最长公共前缀为 \(x\)(废话),也就意味着有 \(\lfloor x/i\rfloor\) 个在 \(i\) 之后且与 \(S_{0,i-1}\) 相等,如图。
(这里直接搬运了洛谷题解的图,果然还是图清晰)。
这样长度为 \(i\) 的循环串最多循环 \(\lfloor next_i/i\rfloor+1\) 次。
这也意味着每个长度为 \(i\) 的循环串,\(C\) 的取值长度有 \(t=\lfloor next_i/i\rfloor+1\) 种。其中 \(i\) 出现奇数次 \(t-t/2\) 种,偶数次 \(t/2\) 种。(反正没人看,这里就不写下取整了)
考虑字符出现次数
容易发现循环串出现次数为奇数时,循环串会在 \(C\) 中出现偶数次,也意味着循环串在 \(C\) 中的部分对 \(C\) 的贡献为 \(0\),所以每个不同的为奇数的字符出现次数,其满足的限制条件实质上是一样的。这里定义 \(f(l,r)\) 为字符串 \(S_{l,r}\) 中出现奇数次的字符的个数。假设 \(|A|=j(j\leq i-1)\)。那么只需要满足
假设满足这样条件的 \(j\) 的个数为 \(cnt\)。那么答案就是 \(cnt_1\times (t-t/2)\) 。
如果循环串出现次数为偶数,同理,其实不难得出 \(j\) 需要满足限制。
答案就是 \(cnt_2\times (t/2)\)。
实现
\(next\) 数组可以使用 Z 函数很快得出,至于 \(f\) 函数的取值,容易发现其要么是从 \(0\) 开始,要么是以 \(n-1\) 结束,所以完全可以开两个桶分别维护 \(f(0,i)\) 和 \(f(i,n-1)\)。每加入一个字符 \(c_i\),就在 \(f(0,i)\) 的桶加入 \(c_i\),\(f(i,n-1)\) 中删除字符,并且要在同时判断奇偶性。
又因为我们是要维护所有满足 \(j\) 的位置的数量,所以可以使用树状数组维护出现次数为奇数的字符的个数的前缀和。(没办法定语太多了,实际上就是树状数组在 \(f(0,j)\) 的位置 \(+1\))
这个树状数组需要维护的下标就是字符集的大小。(理解了这点上面的读不明白也就明白了)
同时因为树状数组的下标不能为 \(0\),无论加入还是查询的时候要将数 \(+1\)。
下面提供一个早期代码(还是树状数组非三行的时代)。
const int N=(1<<20)+5;
char s[N];int len,z[N];//字符串,字符串长度,z函数
int bot1[30],bot2[30];//两个桶记录当前位置左侧和右侧字符出现次数
int pre,suf,all;//当前位置前缀,后缀和整个字符数组中出现奇数次字符的个数
ll ans=0;
struct BIT{//树状数组Binary Indexed Tree
int c[30];
void clears(){memset(c,0,sizeof(c));}
ll lowbit(int x){return x&-x;}
ll getsum(int x){int ans=0;
for(;x>0;x-=lowbit(x))ans+=c[x];
return ans;
}
void update(int x){
for(;x<=25;x+=lowbit(x))++c[x];
}
}tree;
void extraKMP(){
z[0]=len;
int now=0,p0=1;
while(now+1<len&&s[now]==s[now+1])++now;
z[1]=now;p0=1;
for(int i=2;i<len;++i){
if(i+z[i-p0]<p0+z[p0])z[i]=z[i-p0];
else{
now=max(p0+z[p0]-i,0);
while(now+i<len&&s[now]==s[now+i])++now;
z[i]=now;p0=i;
}
}
}
int main(){
int T;scanf("%d",&T);
while(T--){
scanf("%s",s);len=strlen(s);
memset(bot1,0,sizeof(bot1));
memset(bot2,0,sizeof(bot2));
tree.clears();
all=pre=suf=0;ans=0;
extraKMP();
for(int i=0;i<len;++i)//如果循环节可以到结尾,-1,留一个空位给C
if(i+z[i]==len)--z[i];
for(int i=0;i<len;++i)++bot1[s[i]-'a'];
for(int i=0;i<26;++i)if(bot1[i]&1)++all;//统计奇数次字符
suf=all;//后缀暂时为总数
for(int i=0;i<len;++i){
if(bot1[s[i]-'a']&1)--suf;//由奇变偶
else ++suf;//由偶变奇
bot1[s[i]-'a']--;//总数-1
if(bot2[s[i]-'a']&1)--pre;
else ++pre;
bot2[s[i]-'a']++;//同样对后缀进行维护
if(i!=0&&i!=len-1){//循环节大于1且不到末尾
int t=z[i+1]/(i+1)+1;//循环节出现的次数
ans+=1ll*(t/2)*tree.getsum(all+1)+1ll*(t-t/2)*tree.getsum(suf+1);
}
tree.update(pre+1);
}
printf("%lld\n",ans);
}
return 0;
}
总结
这题本身考察面比较广,需要对各个环节的掌握都足够流畅,难度还是挺大的。同时将一个限制较多的复杂问题转化成多个限制较少的相对容易的问题,再结合起来,从这题中能得到很大启发。
UVA11475 Extend to Palindrome
对于字符串 \(S\),求出最短的一个串 \(S'\) 满足 \(S'\) 是回文串,且 \(S\) 是 \(S'\) 的一个前缀。
小清新字符串题,解法众多。
题解
抛开最短的限制不谈,可以发现去将 \(S\) 翻转后接在原 \(S\) 的后方,那么一定能满足回文串和前缀两个限制。
定义 \(T\) 为翻转后的串。
S : abbcb
T : bcbba
S': abbcbbcbba = S+T
会发现如果 \(T\) 的前缀和 \(S\) 的一段后缀相等,那么可以去掉 \(S\) 的这段后缀,这样去除的部分是一个回文串,而去除后的 \(S'\) 也是回文串。这个过程就是一个 \(Z\) 函数的过程。
其实如果发现了这一点的话,可以直接在原串中求最长的回文后缀,直接 manacher 搞就行了。。。
但是因为因为 \(Z\) 函数的题太少了,必须要找一题来凑数,所以我还使用 \(Z\) 函数写的(贼长,不如马拉车)。
char s[N],t[N];
int n,nxt[N],ext[N];
inline void init(){
for(int i=0;i<n;++i)nxt[i]=ext[i]=0;
}
void getnext(){
nxt[0]=n;int now=0,p0=1;
while(t[now]==t[now+1]&&now+1<n)++now;
nxt[1]=now;
for(int i=2;i<n;++i){
if(i+nxt[i-p0]<p0+nxt[p0])nxt[i]=nxt[i-p0];
else{
now=max(p0+nxt[p0]-i,0);
while(t[now]==t[i+now]&&i+now<n)++now;
nxt[i]=now;p0=i;
}
}
}
void funcZ(){
int now=0,p0=0;
while(s[now]==t[now]&&now<n)++now;
ext[0]=now;
for(int i=1;i<n;++i){
if(i+nxt[i-p0]<p0+ext[p0])ext[i]=nxt[i-p0];
else{
now=max(p0+ext[p0]-i,0);
while(t[now]==s[i+now]&&i+now<n)++now;
ext[i]=now;p0=i;
}
}
}
int main(){
while(scanf("%s",s)!=EOF){
n=strlen(s);
for(int i=0;i<n;++i)
t[i]=s[n-i-1];
init();
getnext();
funcZ();
for(int i=0;i<n;++i){
if(i+ext[i]==n){
for(i=0;i<n;++i)
putchar(t[i]);
break;
}
putchar(s[i]);
}putchar('\n');
}
return 0;
}
LG8112 [Cnoi2021]符文破译
给定两个串 \(T\),\(S\)。现在将 \(S\) 划分为多个为 \(T\) 前缀的子串。求最少划分的子串数,如果不能够划分,输出
Fake。数据范围:\(|S|,|T|\leq 10^7\)
题解
考虑使用动态规划,正着 dp 难以转移到后继状态复杂,考虑倒着 dp。设 \(dp_i\) 表示 \(S_{i,n}\) 的最少划分数,\(ext_i\) 为 \(S_{i,n}\) 与 \(T\) 的最长公共前缀。则
\(ext\) 直接 Z函数求。这样 \(O(n^2)\) 就暴力扫,\(O(n\log n)\) 就数据结构维护区间最小值。但均不足以通过。考虑 \(O(n)\) 的做法。
容易发现如果 \(i<i'\) 且 \(i+ext_i>i'+ext_{i'}\),那么从 \(i'\) 划分一定不优秀,可以直接不考虑 \(i'\)。这样子以后 \(f(i)=i+ext_i\) 实际上就是单调的了,然后使用单调队列优化即可。
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N=10000007,INF=0x3f3f3f3f;
int n,m,tot,nxt[N],ext[N],dp[N];
char s[N],t[N];
int q[N],head,tail;
int main(){
scanf("%d%d%s%s",&n,&m,t+1,s+1);
nxt[1]=n;
for(int i=2,l=0,r=0;i<=n;++i){
if(i<=r)nxt[i]=min(r-i+1,nxt[i-l+1]);
else nxt[i]=0;
while(i+nxt[i]<=n&&t[1+nxt[i]]==t[i+nxt[i]])++nxt[i];
if(r<i+nxt[i]-1)l=i,r=i+nxt[i]-1;
}
for(int i=1,l=0,r=0;i<=m;++i){
if(i<=r)ext[i]=min(r-i+1,nxt[i-l+1]);
else ext[i]=0;
while(t[1+ext[i]]==s[i+ext[i]]&&i+ext[i]<=m&&1+ext[i]<=n)++ext[i];
if(r<i+ext[i]-1)l=i,r=i+ext[i]-1;
}
memset(dp,0x3f,sizeof(dp));
dp[m+1]=0,q[head=tail=1]=m+1;
for(int i=1,j=0;i<=m;++i)j>i+ext[i]?ext[i]=INF:j=i+ext[i];
//这些一定不优的决策点必须去除,不然在单调队列中他们会将合法的q[head] pop 掉
for(int i=m;i>=1;--i){
if(ext[i]==INF)continue;
while(head<=tail&&q[head]>i+ext[i])++head;
dp[i]=dp[q[head]]+1;
while(head<=tail&&dp[q[tail]]>=dp[i])--tail;
q[++tail]=i;
}
if(dp[1]>=INF)puts("Fake");
else printf("%d\n",dp[1]);
return 0;
}
// 205ms / 128.32MB / 1.26KB C++14 (GCC 9) O2
本文作者:BigSmall_En
本文链接:https://www.cnblogs.com/BigSmall-En/p/16537930.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 一个费力不讨好的项目,让我损失了近一半的绩效!
· 实操Deepseek接入个人知识库
· CSnakes vs Python.NET:高效嵌入与灵活互通的跨语言方案对比
· 【.NET】调用本地 Deepseek 模型
· Plotly.NET 一个为 .NET 打造的强大开源交互式图表库