CF765F 题解
CF765F Solution
大牛逼分块线段树题。
给出 \(n\) 以及一个长为 \(n\) 的序列 \(a\)。给出 \(m\) 组询问。
每组询问给出一个 \(l,r\),需要求出对于 \(i,j\in[l,r]\),且满足 \(i\neq j,|a_i-a_j|\) 的最小值。
\(1\leq n\leq 10^5,1\leq m\leq 3\times10^5,0\leq a_i\leq 10^9\)
题解
做法来自神仙
不强制在线,考虑将询问离线。
发现按照右端点排序,对于每个右端点 \(r\),维护一个 \(ans_i=\min|a_i-a_j|,j\in[i,r]\)。
对于询问 \([l,r]\),答案就是 \(l\) 的后缀最小值。这个过程暴力做是 \(O(n^2)\) 的。
既然是后缀最小值,那么对于 \(ans_i\),它的值是否是 \(\min|a_i-a_j|\) 就没那么重要了,实际上,我们只需要保证 \(ans_{i\sim r}\) 中的答案是最优的即可。
考虑将右端点从 \(r-1\) 移动到 \(r\),已经维护好了右端点 \(r-1\) 时的 \(ans\) 满足 \([l,r]\) 的答案就是 \(ans\) 的一段后缀最小值。
证明:对于每个 \(ans_i\),只有 \(\log a_i\) 个位置让这个位置的答案必须被修改。
见图
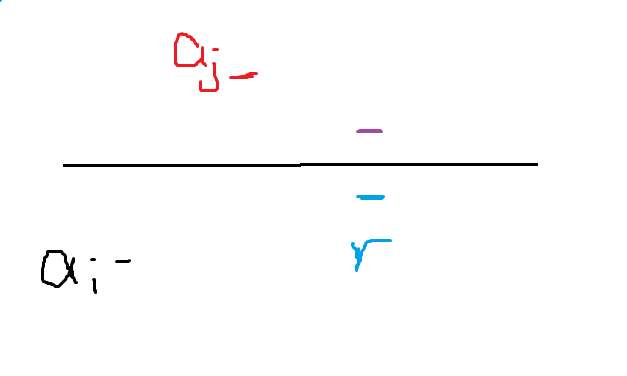
假设目前的答案最优是 \(a_j-a_r\),中间的黑线为 \((a_i+a_j)/2\)。
- \(a_r<mid\),那么最优答案更新为 \(a_r-a_i\),\(ans_i\) 的值减少到至少一半。
- \(a_r\geq mid\),那么最优答案仍然是 \(a_j-a_r\),\(ans_i\) 的值不用被修改,只需修改 \(ans_j\) 的值,同时 \(ans_j\) 的值也减半了。
对于其他的情况也是类似的。
至于如何实现修改时跳过的操作呢。
可以考虑用线段树处理区间信息,同时处理顺序从右往左(因为维护后缀最小值,如果左侧的区间的最优答案都没右侧小,那么左区间不用递归)。
至于如何得出区间最优答案,建树时用一个 vector 存下该区间的所有的数,并队 vector 排序,查找时只用二分即可。
建树的时间复杂度是 \(O(n\log^2 n)\),因为每个点最多被修改 \(\log_a\) 次,所以查询时总的时间复杂度 \(O(n\log n\log a)\)。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
inline int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||'9'<ch){if(ch=='-')f=-1;ch=getchar();}
while('0'<=ch&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*f;
}
const int N=300005,INF=0x3f3f3f3f;
int n,m,a[N];
struct querys{int l,r,id;}que[N];
inline bool cmp(querys x,querys y){
return x.r==y.r?x.l<y.l:x.r<y.r;
}
#define ls p<<1
#define rs p<<1|1
#define mid ((l+r)>>1)
vector<int>lis[N<<2];
int minv[N<<2],lim,ans[N];
inline void pushup(int p){minv[p]=min(minv[ls],minv[rs]);}
void build(int p,int l,int r){
minv[p]=INF;
for(int i=l;i<=r;++i)lis[p].push_back(a[i]);
sort(lis[p].begin(),lis[p].end());
if(l==r)return;
build(ls,l,mid);build(rs,mid+1,r);
pushup(p);
}
void update(int p,int l,int r,int R,int x){
if(1<=l&&r<=R){
auto it=lower_bound(lis[p].begin(),lis[p].end(),x);
if(it!=lis[p].end())minv[p]=min(minv[p],*it-x);
if(it!=lis[p].begin())minv[p]=min(minv[p],x-*(it-1));
if(minv[p]>=lim)return;
}
if(l==r){lim=min(lim,minv[p]);return;}
if(R>mid)update(rs,mid+1,r,R,x);//先改右区间再改左区间可以剪枝
update(ls,l,mid,R,x);
pushup(p);lim=min(lim,minv[p]);
}
int query(int p,int l,int r,int L){
if(L<=l&&r<=n)return minv[p];
int tmp=INF;
if(L<=mid)tmp=min(tmp,query(ls,l,mid,L));
tmp=min(tmp,query(rs,mid+1,r,L));
return tmp;
}
int main(){
n=read();
for(int i=1;i<=n;++i)a[i]=read();
m=read();
for(int i=1;i<=m;++i)que[i].l=read(),que[i].r=read(),que[i].id=i;
sort(que+1,que+1+m,cmp);
build(1,1,n);
int loc=1;
while(que[loc].r<=1)++loc;
for(int i=2;i<=n;++i){
lim=INF;
update(1,1,n,i-1,a[i]);
while(que[loc].r==i){
ans[que[loc].id]=query(1,1,n,que[loc].l);
++loc;
}
}
for(int i=1;i<=m;++i)printf("%d\n",ans[i]);
return 0;
}
本文作者:BigSmall_En
本文链接:https://www.cnblogs.com/BigSmall-En/p/16533543.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步