联机游戏玩家卡顿概率分析
比较联机游戏不同玩家数量时,卡顿的概率。
比如六人联机卡顿概率是三人联机的几倍(其实这是我思考这个问题的出发点。
问题简化:
假设一个玩家网络卡顿的概率为p, 且0<=p<=1。
那么n个玩家联机打一局游戏,遇到卡顿的概率是多少?
说明1:只要有一个玩家卡顿就算这局游戏卡顿。
说明2: n>=2,因为一人单机不用联网。
分析与求解
直接去计算卡顿是很麻烦的,
因为要考虑多种情况:
- 1个玩家卡顿
- 2个玩家卡顿
...... - n个玩家卡顿
正难则反
我们从该问题的反向情况思考,
即没有玩家卡顿的概率是多少,再用1一减。
那么就很简单,一个玩家不卡顿的概率是\(1-p\),
n个玩家都不卡顿的概率是\((1-p)^n\)
所以遇到卡顿的概率如下
\[P = 1 - (1-p)^n
\]
这个展开写的话,有点麻烦了,就不详细展开了。
接下来我们要探究的是不同人数的卡顿概率问题
深入探究
总体数据变化
对于固定的n,这个最终结果受到变量p的影响。
把这个写成函数形式如下
\[P_n(p) = 1 - (1-p)^n
\]
那么n取2,3,4,5,6时,对应的函数如下
\[P_2(p) = 1 - (1-p)^2\\
P_3(p) = 1 - (1-p)^3\\
P_4(p) = 1 - (1-p)^4\\
P_5(p) = 1 - (1-p)^5\\
P_6(p) = 1 - (1-p)^6\\
\]
我们首先看下,n在这些值时,
\(P_n\)与变量p的变化关系。
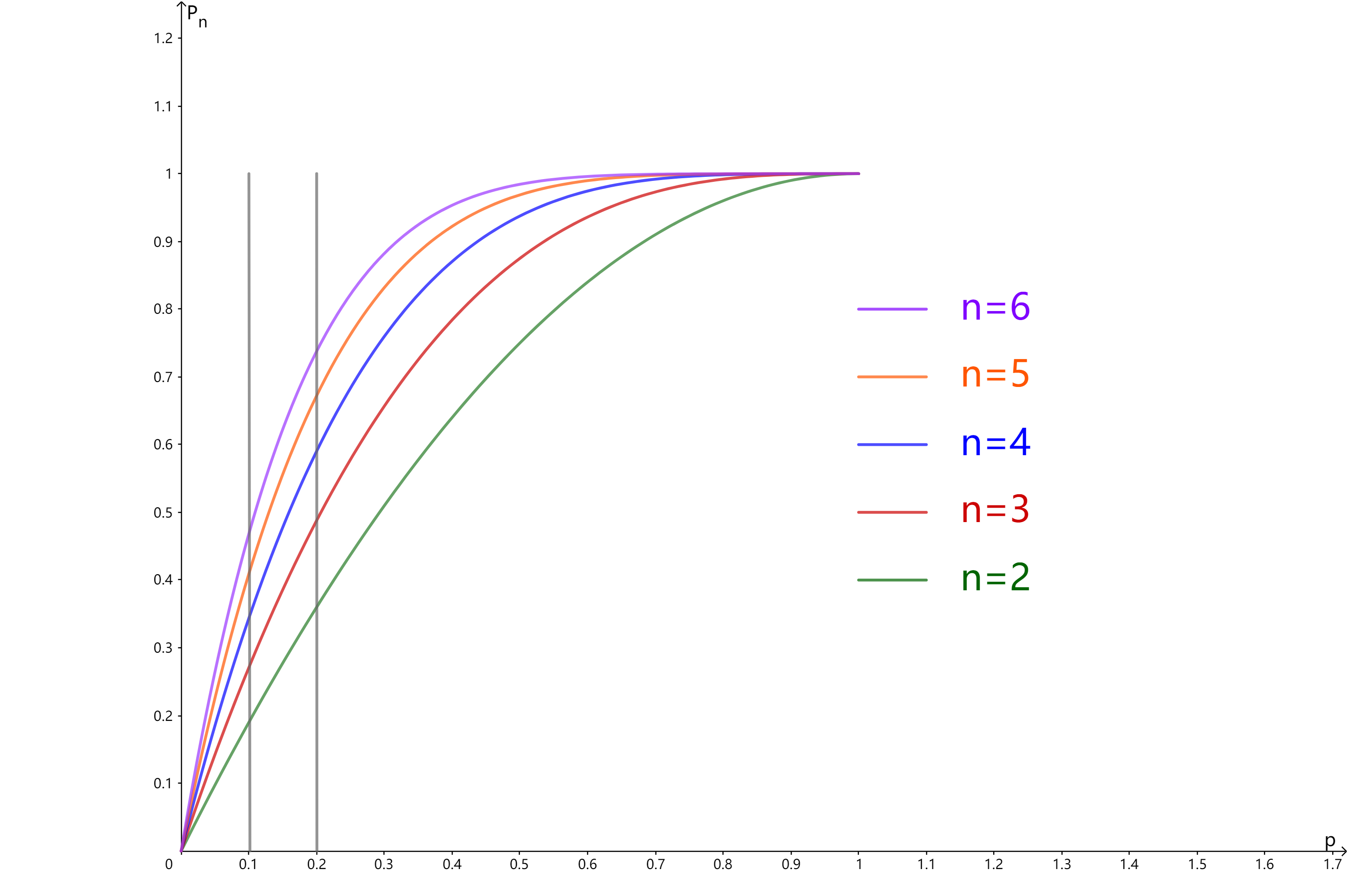
不同n值的差别在p比较小的时候很明显,但是差距好像也不是很大,起码比我预想中的要小。
以p=0.1为例,
\[P_2 = 0.19 \\
P_3 = 0.27 \\
P_4 = 0.34 \\
P_5 = 0.41 \\
P_6 = 0.47
\]
\(P_6\)约是\(P_2\)的2.5倍左右
不过数据比例关系在这个图中感觉还是不够直观,尤其是p<0.1时,太小看不清。
6v3
下面专门来看看六玩家卡顿概率是三玩家卡顿概率的多少倍。
\[\begin{aligned}
M_{6-3} &= \frac {P_6(p)} {P_3(p)} =
\frac {1 - (1-p)^6} {1 - (1-p)^3} \\
&= \frac {(1 - (1-p)^3)(1 + (1-p)^3)} {1 - (1-p)^3} &\text{平方差公式}\\
&= (1 + (1-p)^3)
\end{aligned}
\]
由于0<p<1,所以
这个倍数关系范围在1-2之间,
具体如下图

6v2
再来看看六玩家卡顿概率是二玩家卡顿概率的多少倍。
\[\begin{aligned}
M_{6-2} &= \frac {P_6(p)} {P_2(p)} =
\frac {1 - (1-p)^6} {1 - (1-p)^2} \\
&= \frac {(1 - (1-p)^2)(1 + (1-p)^2 + (1-p)^4 )} {1 - (1-p)^2} &\text{立方差公式} \\
&= 1 + (1-p)^2 + (1-p)^4
\end{aligned}
\]
由于0<p<1,所以
这个倍数关系范围在1-3之间,
其图像如下

结论
- 6玩家卡顿概率,最多是3玩家卡顿概率的两倍
- 6玩家卡顿概率,最多是2玩家卡顿概率的3倍
由于p=0时,P都为0, 所以实际上最大值达不到。


