数据结构(四十四)交换排序(1.冒泡排序(O(n²))2.快速排序(O(nlogn))))
一、交换排序的定义
利用交换数据元素的位置进行排序的方法称为交换排序。常用的交换排序方法有冒泡排序和快速排序算法。快速排序算法是一种分区交换排序算法。
二、冒泡排序
1.冒泡排序的定义
冒泡排序(Bubble Sort)是一种交换排序,它的基本思想是:两两比较相邻记录的关键字,如果反序则交换,直到没有反序的记录为止。
2.冒泡排序的实现
(1)非标准冒泡排序算法--最简单的交换排序

思想就是让每一个关键字,都和它后面的每一个关键字比较,如果大则交换,这样第一位置的关键字在一次循环后一定变成最小值。
然而缺陷就是,在排序号1和2之后,数字3反而到了最后一位。
// 不是标准的冒泡排序算法,因为它不满足"两两比较相邻记录"的冒泡排序思想,是最简单的交换排序而已。 public static void BubbleSort0(int[] L) { for (int i = 0; i < L.length; i++) { for (int j = i + 1; j < L.length; j++) { if (L[i] > L[j]) { Assistant_And_Test.swap(L, i, j); } } } }
int[] array2 = {9,1,5,8,3,7,4,6,2};
当i=0时,9与1交换,因为1比其他位置的数字都小,所以1在第0位
当i=1时,9与5交换,5与3交换,3与2交换,所以2在第1位
...
(2)标准冒泡排序算法

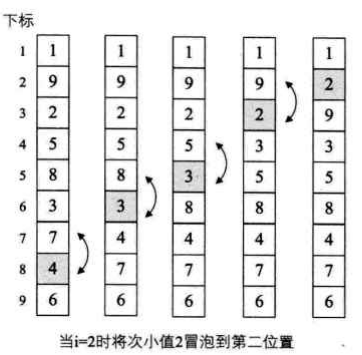
// 标准的冒泡排序算法 public static void BubbleSort1(int[] L) { for (int i = 0; i < L.length; i++) { for (int j = L.length - 2; j >= i; j--) { if (L[j] > L[j + 1]) { swap(L, j, j + 1); } } } }
int[] array2 = {9,1,5,8,3,7,4,6,2};
当i=0时,j从7开始,6与2交换,4与2交换,7与2交换,3与2交换,8与2交换,5与2交换,9与1交换,1排在第0位,2的位置也上升了
当i=1时,j从7开始,7与4交换,8与3交换,9与2交换,2排在第1位,3和4的位置也上升了
...
(3)改进的冒泡排序
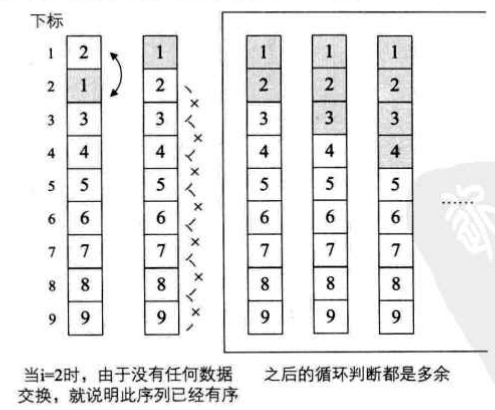
假设待排序的序列为{2,1,3,4,5,6,7,8,9},当i=0时,交换2和1,此时序列已经有序,但是算法仍然将i=1到8以及每个循环中的j循环都执行了一遍,尽管并没有交换数据,但是之后的大量比较还是大大多余了。因此,增加一个标记变量flag来实现这一算法的改进。
// 改进的冒泡排序算法,增加一个标记变量flag public static void BubbleSort2(int[] L) { boolean flag = true; // 用flag来做标记 for (int i = 0; i < L.length && flag; i++) { flag = false; // 初始值为false for (int j = L.length - 2; j >= i; j--) { if (L[j] > L[j + 1]) { swap(L, j, j + 1); flag = true;// 如果有数据交换,则flag为true } } } }
int[] array3 = {2,1,3,4,5,6,7,8,9};
i=0,flag=false,j=7开始,8和9不交换,7和8不交换,...2和1交换,flag=true,进入for循环
i=1,flag=false,j=7开始,没有交换的,所以flag仍然等于false,不进入for循环,
...
3.冒泡排序算法的性能分析
(1)时间复杂度O(n²)
对于改进的冒泡排序来说,最好的情况,如果待排序的序列本身就是有序的,那么需要比较n-1次,交换0次,时间复杂度为O(n)。
最坏的情况,即待排序的序列是逆序的情况下,此时需要比较1+2+3+...+(n-1) = n(n-1)/2次,并移动n(n-1)/2次,所以总的时间复杂度为O(n²)。
(2)空间复杂度为O(1)。
(3)是一种稳定的排序算法。
三、快速排序
一、快速排序算法的定义
快速排序算法的基本思想是:通过一趟排序将待排序记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,则可分别对这两部分进行排序,以达到整个序列有序的目的。
二、快速排序算法的设计
快速排序算法是一种二叉树结构的交换排序方法。设数组a存放了n个数据元素,low为数组的低端下标,high为数组的高端下标,从数组a中任取一个元素作为标准元素,以该标准元素调整数组a中其他各个元素的位置,使排在标准元素前面的元素均小于标准元素,使排在标准元素后面的元素均大于或等于标准元素。这样一次排序过程后,一方面将标准元素放在了未来排好序的数组中该标准元素应位于的位置上,另一方面将数组中的元素以标准元素为中心分成两个子数组,位于标准元素左边子数组中的元素均小于标准元素,位于标准元素右边子数组中的元素均大于或等于标准元素。对这两个子数组中的元素分别再进行方法类似的递归快速排序。算法递归出口条件是low≥high。
三、快速排序算法的实现
1.快速排序算法的实现
public static void quickSort(int[] a, int low, int high) { int i, j; int temp; i = low; j = high; temp = a[low]; while (i < j) { while (i < j && temp <= a[j]) { // 从上限high起,如果大于temp就位置不变 j--; // 寻找比temp小的数的数组下标 } if (i < j) { // 将比temp小的数放在temp坐标的i位置上 a[i] = a[j]; i++; } while (i < j && temp > a[i]) { // 从下限low起,如果小于temp就位置不变 i++; // 寻找比temp大的数的数组下标 } if (i < j) { // 将比temp的数放在temp坐标的i位置上 a[j] = a[i]; j--; } } a[i] = temp; // if (low < i) { quickSort(a, low, i - 1); } if (i < high) { quickSort(a, j+1, high); } }
2.结合代码分析执行过程
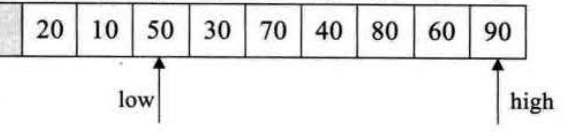
int[] array1 = {50,10,90,30,70,40,80,60,20}; temp=a0=50,
i=0,j=8,0<8进入while循环:temp=50,a8=20,不进while;0<8,a[0]=20,i=1;50>10,i=2,50<90,跳出while,a8=a2=90,j=7,数组为[20,10,90,30,70,40,80,60,90]
i=2,j=7,2<7进入while循环:temp=50,a7=60,进入while;j=5,2<5,a2=a5=40,i=3;temp=50>a3=30,i=4,4<5,a5=a4=70,j=4,跳出while,a4=50,数组为[20,10,40,30,50,70,80,60,90]
具体过程可以总结为:
首先将50取出放入temp中,
此时low为0,high为8,从high开始寻找比50小的数20,high为8,,然后将20放到0的位置上,即a0为20,并把low加上1为1,此时数组为[20,10,90,30,70,40,80,60,20]
此时low为1,high为8,从low开始寻找比50大的数90,low为2,然后将90放到8的位置上,即a8为90,并把high减去1为7,此时数组为[20,10,90,30,70,40,80,60,90]
此时low为2,high为7,从high开始寻找比50小的数,找到了40,则high为5,然后把40放到low的位置上,即a2为40,并把low加上1为3,此时数组为[20,10,40,30,70,40,80,60,90]
此时low为3,high为5,从low开始寻找比50大的数,找到了70,则low为4,然后把70放到high的位置上,即a5为70,并把high减1为4,此时数组为[20,10,40,30,70,70,80,60,90]
此时low为4,high为4,循环结束,a4=temp=50,此时数组为[20,10,40,30,50,70,80,60,90]
即此次过程实现了将50左右两个子数组分开,形成两个子数组{20,10,40,30}和{70,80,60,90},
然后执行quickSort(a,0,4);和quickSort(a,5,8);,即对{20,10,40,30}和{70,80,60,90}分别进行相同的操作。
用图片展示执行过程:
(1)
(2)
(3)
(4)
(5)
(6)
3.测试代码和输出
public static void main(String[] args) { int[] array1 = {50,10,90,30,70,40,80,60,20}; System.out.print("大顶堆创建前: "); print(array1); quickSort(array1, 0, array1.length - 1); System.out.print("大顶堆创建后: "); print(array1); } 快速排序前: 50 10 90 30 70 40 80 60 20 快速排序后: 10 20 30 40 50 60 70 80 90
四、快速排序算法的性能分析
(1)时间复杂度
- 最优情况下
快速排序算法的时间复杂度和各次标准数据元素的取法关系很大。
最好情况是,如果每次选取的标准元素都能均分两个子数组的长度,这样的快速排序算法过程就是一个完全二叉树结构(即每次标准元素都把当前数组分成两个大小相等的子数组)。
例如
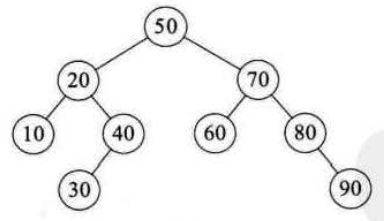
由于第一个关键字是50,正好是待排序序列的中间值,因此此时性能是最好的。
在最好的情况下,如果有n个关键字,那么其对应的完全二叉树的深度为【logn】+1,即仅需递归log2n次。
假设第一次递归需要T(n)的时间的话,那么将数组一分为二后各自还需要T(n/2)的时间。
同时,又由于不管如何分组,每次递归都需要比较n-1次,所以有:
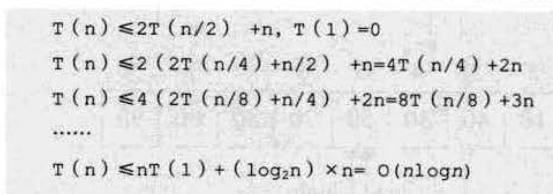
从而,在最优情况下,快速排序算法的时间复杂度为O(nlogn)。(简单来说可以这么记,需要递归log2n次,每次需要比较n次,总时间即为O(nlogn))。
- 最坏情况下
最坏情况就是待排序的序列为正序或者反序,每次划分只得到一个比上一次划分少一个记录的子序列,另一个为空。
此时对应的二叉树就是一颗斜树,需要执行n-1次递归调用,且第i次划分需要经过n-i次比较才能找到第i个记录,因此比较的次数为n-1 + n-2 +... +1=n(n-1)/2,因此时间复杂度为O(n²)。
- 平均情况下
平均情况下,数据元素的分布是随机的,数组分解构成的二叉树的深度接近于logn,所以平均时间复杂度为O(nlogn))。
(2)空间复杂度
快速排序算法的空间复杂度主要是由于需要堆栈空间临时保存递归调用参数,堆栈空间的使用个数和递归调用的次数,也就是二叉树的深度有关。
因此最好情况下空间复杂度为O(logn),最坏情况需要n-1次递归,即空间复杂度为O(n),同理,平均情况下空间复杂度为O(logn)。
(3)稳定性
由于关键字的比较和交换是跳跃进行的,因此,快速排序是一种不稳定的排序方法。
五、快速排序算法的优化分析
1.对于temp的选取,为了保证取到接近中间值的关键字。可以有三数取中法,即取三个关键字先进行排序,将中间数作为枢轴,一般是去左、中和右三个数,也可以随机选取。还有九数取中法,即先从数组中分三次取样,每次取三个数,三个样品各取出中数,然后从这三个数中再取出一个中数作为枢轴。
2.对于非常大量的数据,快速排序性能比直接插入排序要好;但是对于非常小的数组,快速排序反而不如直接插入排序性能好。这是因为快速排序用到了递归操作,在大量数据排序时,这点性能的影响相对于它的整体算法优势而言是可以忽略的,如果数组只有几个记录需要排序,就可以使用直接插入排序而不是快速排序。
可以这样设计:
if ((high - low)> 一个值){ 使用快速排序} else { 使用直接插入排序 }
3.优化递归操作,如果待排序的序列划分极其不平衡,就可以通过增加判断语句,将划分之后数量少的一部分使用直接插入排序,而数量多的那部分继续使用快速选择排序的递归算法。




