数据结构（三十九）二叉排序树

　　一、二叉排序树的定义

　　在静态查找的几种方法中，二分查找具有最高的查找效率，但是由于二分查找要求表中记录按关键字有序，且不能用链表做存储结构，因此，当表的插入、删除操作非常频繁时，为维护表的有序性，需要移动表中很多记录。这种由移动记录引起的额外时间开销，就会抵消二分查找的有限。而二叉排序树不仅具有二分查找的效率，同时又便于插入和删除操作。

　　二叉排序树（Binary Sort Tree），又称为二叉查找树。它或者是一棵空树，或者是具有下列性质的二叉树。

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若它的右子树不空，则右子树上所有节点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉排序树

　　对二叉排序树进行中序遍历就可以得到一个有序的序列{35,37,47,51,58,62,73,88,93,99}

 

　　二、二叉排序树的查找

　　若将查找表组织为一棵二叉排序树，则根据二叉排序树的特点，查找过程的主要步骤归纳如下：

• 若查找树为空，则查找失败；
• 若查找树为非空，则：

　　①若给定值key等于根结点的关键字值，则查找成功，结束查找过程，否则转②

　　②若给定值key小于根结点的关键字值，则继续在根结点的左子树上进行，否则转③

　　③若给定值key大于根结点的关键字值，则继续在根结点的右子树上进行。

    // 在二叉排序树p中查找key，若查找成功返回true，查找不成功返回false
    // 返回false有两种情况:1.二叉排序树p为空 2.二叉排序树p不为空但是没有查找到key
    public boolean searchBST(int key) {
        BiTreeNode current = root;
        while (current != null) {
            if (key == current.data) {
                return true;
            } else if (key < current.data) {
                current = current.lchild;
            } else {
                current = current.rchild;
            }
        }
        return false;
    }

 

　　三、二叉排序树的插入

　　假设待插入结点的关键字值为key，为了将其插入到表中，先要将它放入二叉排序树中进行查找，若查找成功，则按二叉排序树定义，带插入结点已存在，不用插入；否则，将新结点插入到表中。因此，新插入的结点一定是作为叶子结点添加到表中去的。

    public void insertBST(int key) {
        BiTreeNode p = root;        　　// 二叉树的根结点
        BiTreeNode prev = null;        　　// 二叉树的双亲结点
        while (p!=null) {            　　// 新插入的结点一定是作为叶子结点添加到树中的
            prev = p;                　　// 记录孩子为空的结点作为新插入结点的双亲
            if (key < p.data) {
                p = p.lchild;
            } else if (key > p.data) {
                p = p.rchild;
            } else {
                return ;
            }
        }
        if (root == null) {
            root = new BiTreeNode(key);
        } else if (key < prev.data) {    // 将新插入的结点作为叶子结点插入到树中
            prev.lchild = new BiTreeNode(key);
        } else {
            prev.rchild = new BiTreeNode(key);
        }
    }

　　以下面的示例分析代码实现过程：

　　

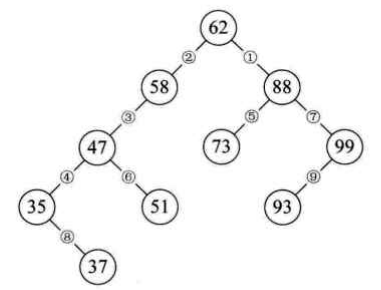
    public static void main(String[] args) {
        BinarySortTree bst = new BinarySortTree();
        int[] a = {62,88,58,47,35,73,51,99,37,93};
        System.out.print("是否插入成功: ");
        for (int i = 0; i < a.length; i++) {
            bst.insertBST(a[i]);
        }

p为null，prev也为null，while循环跳过，进入if循环，root为62
p为62，prev=null，进入while循环，prev=62,88>62，p为62的右孩子为空，进入if循环，62的右孩子为88
p为62，prev=null，进入whlie循环，prev=62,58<62,p为62的左孩子为空，进入if循环，62的左孩子为58
p为62，prev=null，进入while循环，prev=62,47<62,p为62的左孩子58，进入while循环，prev=58,47<58,p为58的左孩子为空，进入if循环，47<58,58的左孩子为47
...

 

　　四、二叉排序树的删除

　　二叉排序树的删除要分为4种情况分析：

• 删除叶子结点。做法是：直接删除该结点。

　　

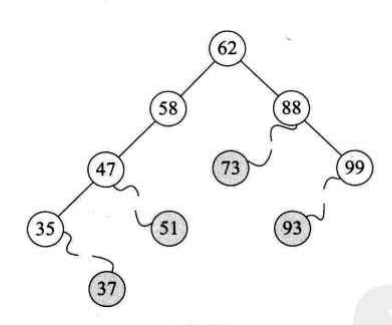
• 删除只有左孩子的结点。做法是：删除该结点且使被删除结点的双亲结点指向被删除节点的左孩子结点。
• 删除只有右孩子的结点。做法是：删除该结点且使被删除结点的双亲结点指向被删除节点的右孩子结点。

　　

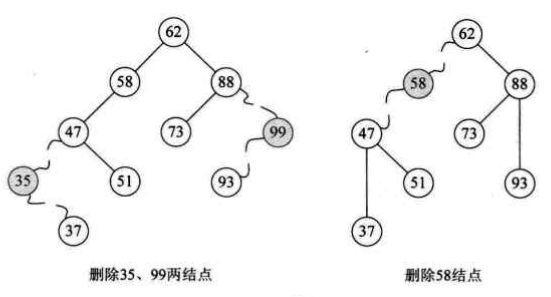
• 删除左孩子和右孩子都有的结点。做法是：首先寻找数据元素值大于要删除结点数据元素关键字的最小值，即寻找要删除结点右子树的最左结点，然后把右子树的最左结点的数据元素复制到要删除的结点上，最后删除右子树的最左结点。（或者左子树的最右结点）

　　

　　二叉树删除操作的实现：

    public boolean deleteBST(BiTreeNode node, int key) {
        if (node == null) {
            return false;
        } else {                            // 要删除的结点为node
            if (key == node.data) {
                return delete(node);
            } else if (key < node.data) {
                return deleteBST(node.lchild, key);
            } else {
                return deleteBST(node.rchild, key);
            }
        }
    }
    
    private boolean delete(BiTreeNode node) {
        BiTreeNode p = null;                // 要删除的结点p
        if (node.rchild == null) {            // 只有左子树
            node = node.lchild;                // 重连左子树
        } else if (node.lchild == null) {    // 只有右子树，
            node = node.rchild;                // 重连右子树
        } else {                            // 左右子树都不为空
            p = node;                        // p是要删除的结点
            BiTreeNode s = node.lchild;        // 寻找左子树
            while (s.rchild != null) {        // 找到左子树的最右结点
                p = s;
                s = s.rchild;
            }
            node.data = s.data;
            if (p != node) {
                p.rchild = s.lchild;
            } else {
                p.lchild = s.lchild;
            }
        }
        return true;
    }

　　结合示例分析删除47结点的执行流程：

　　

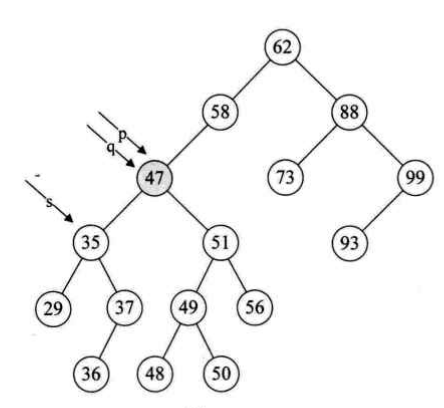
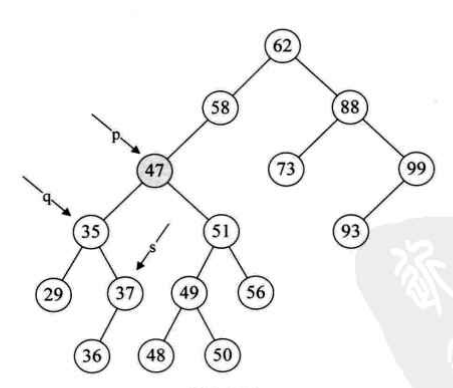
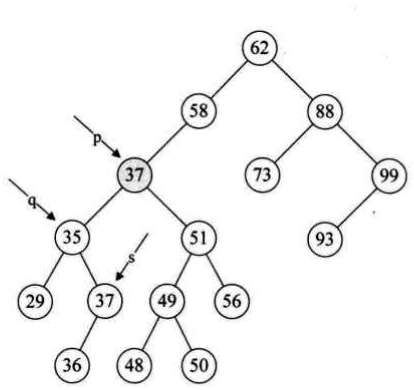
首先通过遍历得到要删除的结点：node=47
然后，p为47，s为47的左孩子35，s的右孩子不为空，此时p为35，s为37,37的右孩子为空，跳出whlie循环
47结点的数据域为37，p此时为35不等于node结点37，因此，35的右孩子此时为37的左孩子，即36，也就是说结点36把结点37顶替掉了，而结点47只是把数据域复制过去了

 

　　五、二叉排序树的查找、插入和删除操作的Java语言代码实现：

• 二叉排序树结点类：

package bigjun.iplab.binarySortTree;
/**
 * 二叉树的结点类
 */
public class BiTreeNode {
    
    public int data;                 // 结点的数据域
    public BiTreeNode lchild, rchild;   // 左孩子和右孩子域
    
    // 构造方法1:构造一个空结点
    public BiTreeNode() {
    }
    
    // 构造方法2:构造一个只有数据域，左、右孩子域都为空的结点
    public BiTreeNode(int data) {
        this(data, null, null);
    }
    
    // 构造方法3:构造一棵数据域和左、右孩子域都不为空的二叉树
    public BiTreeNode(int data, BiTreeNode lchild, BiTreeNode rchild) {
        this.data = data;
        this.lchild = lchild;
        this.rchild = rchild;
    }

}

• 二叉排序树实现类：

package bigjun.iplab.binarySortTree;

public class BinarySortTree {

    private BiTreeNode root = null;
        
    public static void inOrderTraverse(BiTreeNode T) {
        if (T != null) {
            inOrderTraverse(T.lchild);
            System.out.print(T.data + " ");
            inOrderTraverse(T.rchild);
        }
    }
    
    // 在二叉排序树p中查找key，若查找成功返回true，查找不成功返回false
    // 返回false有两种情况:1.二叉排序树p为空 2.二叉排序树p不为空但是没有查找到key
    public boolean searchBST(int key) {
        BiTreeNode current = root;
        while (current != null) {
            if (key == current.data) {
                return true;
            } else if (key < current.data) {
                current = current.lchild;
            } else {
                current = current.rchild;
            }
        }
        return false;
    }

    
    public void insertBST(int key) {
        BiTreeNode p = root;        // 二叉树的根结点
        BiTreeNode prev = null;        // 二叉树的双亲结点
        while (p!=null) {            // 新插入的结点一定是作为叶子结点添加到树中的
            prev = p;                // 记录孩子为空的结点作为新插入结点的双亲
            if (key < p.data) {
                p = p.lchild;
            } else if (key > p.data) {
                p = p.rchild;
            } else {
                return ;
            }
        }
        if (root == null) {
            root = new BiTreeNode(key);
        } else if (key < prev.data) {    // 将新插入的结点作为叶子结点插入到树中
            prev.lchild = new BiTreeNode(key);
        } else {
            prev.rchild = new BiTreeNode(key);
        }
    }
    
    public boolean deleteBST(BiTreeNode node, int key) {
        if (node == null) {
            return false;
        } else {                            // 要删除的结点为node
            if (key == node.data) {
                return delete(node);
            } else if (key < node.data) {
                return deleteBST(node.lchild, key);
            } else {
                return deleteBST(node.rchild, key);
            }
        }
    }
    
    private boolean delete(BiTreeNode node) {
        BiTreeNode p = null;                // 要删除的结点p
        if (node.rchild == null) {            // 只有左子树
            node = node.lchild;                // 重连左子树
        } else if (node.lchild == null) {    // 只有右子树，
            node = node.rchild;                // 重连右子树
        } else {                            // 左右子树都不为空
            p = node;                        // p是要删除的结点
            BiTreeNode s = node.lchild;        // 寻找左子树
            while (s.rchild != null) {        // 找到左子树的最右结点
                p = s;
                s = s.rchild;
            }
            node.data = s.data;
            if (p != node) {
                p.rchild = s.lchild;
            } else {
                p.lchild = s.lchild;
            }
        }
        return true;
    }
    
    public static void main(String[] args) {
        BinarySortTree bst = new BinarySortTree();
        int[] a = {62,88,58,47,35,73,51,99,37,93,29,36,37,48,49,50,56,89};
        System.out.print("插入前，遍历二叉排序树得到的序列为: ");
        inOrderTraverse(bst.root);
        for (int i = 0; i < a.length; i++) {
            bst.insertBST(a[i]);
        }
        System.out.println();
        System.out.print("插入后，中序遍历二叉排序树得到的序列为: ");
        inOrderTraverse(bst.root);
        System.out.println();
        System.out.print("查找二叉排序树中是否有73: ");
        System.out.println(bst.searchBST(73));
        bst.deleteBST(bst.root, 47);
        System.out.print("删除47后，中序遍历二叉排序树得到的序列为: ");
        inOrderTraverse(bst.root);
    }
}

• 输出：

插入前，遍历二叉排序树得到的序列为: 
插入后，中序遍历二叉排序树得到的序列为: 29 35 36 37 47 48 49 50 51 56 58 62 73 88 89 93 99 
查找二叉排序树中是否有73: true
删除47后，中序遍历二叉排序树得到的序列为: 29 35 36 37 48 49 50 51 56 58 62 73 88 89 93 99 

 

　　六、二叉排序树的查找、插入和删除操作的C语言代码实现：

#include "stdio.h"    
#include "stdlib.h"   
#include "io.h"  
#include "math.h"  
#include "time.h"

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 100 /* 存储空间初始分配量 */

typedef int Status;    /* Status是函数的类型,其值是函数结果状态代码，如OK等 */ 

/* 二叉树的二叉链表结点结构定义 */
typedef  struct BiTNode    /* 结点结构 */
{
    int data;    /* 结点数据 */
    struct BiTNode *lchild, *rchild;    /* 左右孩子指针 */
} BiTNode, *BiTree;


/* 递归查找二叉排序树T中是否存在key, */
/* 指针f指向T的双亲，其初始调用值为NULL */
/* 若查找成功，则指针p指向该数据元素结点，并返回TRUE */
/* 否则指针p指向查找路径上访问的最后一个结点并返回FALSE */
Status SearchBST(BiTree T, int key, BiTree f, BiTree *p) 
{  
    if (!T)    /*  查找不成功 */
    { 
        *p = f;  
        return FALSE; 
    }
    else if (key==T->data) /*  查找成功 */
    { 
        *p = T;  
        return TRUE; 
    } 
    else if (key<T->data) 
        return SearchBST(T->lchild, key, T, p);  /*  在左子树中继续查找 */
    else  
        return SearchBST(T->rchild, key, T, p);  /*  在右子树中继续查找 */
}


/*  当二叉排序树T中不存在关键字等于key的数据元素时， */
/*  插入key并返回TRUE，否则返回FALSE */
Status InsertBST(BiTree *T, int key) 
{  
    BiTree p,s;
    if (!SearchBST(*T, key, NULL, &p)) /* 查找不成功 */
    {
        s = (BiTree)malloc(sizeof(BiTNode));
        s->data = key;  
        s->lchild = s->rchild = NULL;  
        if (!p) 
            *T = s;            /*  插入s为新的根结点 */
        else if (key<p->data) 
            p->lchild = s;    /*  插入s为左孩子 */
        else 
            p->rchild = s;  /*  插入s为右孩子 */
        return TRUE;
    } 
    else 
        return FALSE;  /*  树中已有关键字相同的结点，不再插入 */
}

/* 从二叉排序树中删除结点p，并重接它的左或右子树。 */
Status Delete(BiTree *p)
{
    BiTree q,s;
    if((*p)->rchild==NULL) /* 右子树空则只需重接它的左子树（待删结点是叶子也走此分支) */
    {
        q=*p; *p=(*p)->lchild; free(q);
    }
    else if((*p)->lchild==NULL) /* 只需重接它的右子树 */
    {
        q=*p; *p=(*p)->rchild; free(q);
    }
    else /* 左右子树均不空 */
    {
        q=*p; s=(*p)->lchild;
        while(s->rchild) /* 转左，然后向右到尽头（找待删结点的前驱） */
        {
            q=s;
            s=s->rchild;
        }
        (*p)->data=s->data; /*  s指向被删结点的直接前驱（将被删结点前驱的值取代被删结点的值） */
        if(q!=*p)
            q->rchild=s->lchild; /*  重接q的右子树 */ 
        else
            q->lchild=s->lchild; /*  重接q的左子树 */
        free(s);
    }
    return TRUE;
}

/* 若二叉排序树T中存在关键字等于key的数据元素时，则删除该数据元素结点, */
/* 并返回TRUE；否则返回FALSE。 */
Status DeleteBST(BiTree *T,int key)
{ 
    if(!*T) /* 不存在关键字等于key的数据元素 */ 
        return FALSE;
    else
    {
        if (key==(*T)->data) /* 找到关键字等于key的数据元素 */ 
            return Delete(T);
        else if (key<(*T)->data)
            return DeleteBST(&(*T)->lchild,key);
        else
            return DeleteBST(&(*T)->rchild,key);
         
    }
}

int main(void)
{    
    int i;
    int a[10]={62,88,58,47,35,73,51,99,37,93};
    BiTree T=NULL;
    
    for(i=0;i<10;i++)
    {
        InsertBST(&T, a[i]);
    }
    DeleteBST(&T,93);
    DeleteBST(&T,47);
    printf("本样例建议断点跟踪查看二叉排序树结构");
    return 0;
}

 

　　七、二叉排序树的时间复杂度

　　二叉排序树是以链表的方式存储，保持了链式存储结构在执行插入或删除操作时不用移动数据元素的优点，只要找到合适的插入和删除的位置后，仅需要修改链接指针即可，插入和删除的时间性能比较好。二叉排序树的查找走的就是根结点到要查找的结点的路径，其比较次数等于给定值的结点在二叉排序树的成熟。

　　

　　如果按照{62,88,58,47,35,73,51,99,37,93}这样的数组，可以构建上图左图中的二叉排序树。但是，如果数组元素的次序从小到大排序，如{35,37,47,51,58,62,73,88,93,99}，则二叉排序树就成了极端的右斜树，同样是查找99，左图只需要两次比较，而右图要10次比较才行。

　　理想的二叉树是比较平衡的，其深度与完全二叉树相同，均为【log2N】+1，那么查找的时间复杂度也就是O(logn)，近似于二分查找。不平衡的极端情况就是斜树，查找时间复杂度为O(n)，等同于顺序查找。如何让二叉树平衡就成为了需要考虑的问题。