数据结构(三十三)最小生成树(Prim、Kruskal)
一、最小生成树的定义
一个连通图的生成树是一个极小的连通子图,它含有图中全部的顶点,但只有足以构成一棵树的n-1条边。
在一个网的所有生成树中,权值总和最小的生成树称为最小代价生成树(Minimum Cost Spanning Tree),简称为最小生成树。
构造最小生成树的准则有以下3条:
- 只能使用该图中的边构造最小生成树
- 当且仅当使用n-1条边来连接图中的n个顶点
- 不能使用产生回路的边
对比两个算法,Kruskal算法主要是针对边来展开,边数少时效率会非常高,所以对于稀疏图有很大的优势;而Prim算法对于稠密图,即边数非常多的情况会更好一些。
二、普里姆(Prim)算法
1.Prim算法描述
假设N={V,{E}}是连通网,TE是N上最小生成树中边的集合。算法从U={u0,u0属于V},TE={}开始。重复执行下面的操作:在所有u属于U,v属于V-U的边(u,v)中找一条代价最小的边(u0,v0)并加入集合TE,同时v0加入U,直到U=V为止。此时TE中必有n-1条边,则T=(V,{TE})为N的最小生成树。
2.Prim算法的C语言代码实现

/* Prim算法生成最小生成树 */ void MiniSpanTree_Prim(MGraph G) { int min, i, j, k; int adjvex[MAXVEX]; /* 保存相关顶点下标 */ int lowcost[MAXVEX]; /* 保存相关顶点间边的权值 */ lowcost[0] = 0;/* 初始化第一个权值为0,即v0加入生成树 */ /* lowcost的值为0,在这里就是此下标的顶点已经加入生成树 */ adjvex[0] = 0; /* 初始化第一个顶点下标为0 */ for(i = 1; i < G.numVertexes; i++) /* 循环除下标为0外的全部顶点 */ { lowcost[i] = G.arc[0][i]; /* 将v0顶点与之有边的权值存入数组 */ adjvex[i] = 0; /* 初始化都为v0的下标 */ } for(i = 1; i < G.numVertexes; i++) { min = INFINITY; /* 初始化最小权值为∞, */ /* 通常设置为不可能的大数字如32767、65535等 */ j = 1;k = 0; while(j < G.numVertexes) /* 循环全部顶点 */ { if(lowcost[j]!=0 && lowcost[j] < min)/* 如果权值不为0且权值小于min */ { min = lowcost[j]; /* 则让当前权值成为最小值 */ k = j; /* 将当前最小值的下标存入k */ } j++; } printf("(%d, %d)\n", adjvex[k], k);/* 打印当前顶点边中权值最小的边 */ lowcost[k] = 0;/* 将当前顶点的权值设置为0,表示此顶点已经完成任务 */ for(j = 1; j < G.numVertexes; j++) /* 循环所有顶点 */ { if(lowcost[j]!=0 && G.arc[k][j] < lowcost[j]) {/* 如果下标为k顶点各边权值小于此前这些顶点未被加入生成树权值 */ lowcost[j] = G.arc[k][j];/* 将较小的权值存入lowcost相应位置 */ adjvex[j] = k; /* 将下标为k的顶点存入adjvex */ } } } }
3.Prim算法的Java语言代码实现
package bigjun.iplab.adjacencyMatrix; /** * 最小生成树之Prim算法 */ public class MiniSpanTree_Prim { private static class CloseEdge{ Object adjVex; // 顶点符号 int lowCost; // 顶点对应的权值 public CloseEdge(Object adjVex, int lowCost) { this.adjVex = adjVex; this.lowCost = lowCost; } } private static int getMinMum(CloseEdge[] closeEdges) { int min = Integer.MAX_VALUE; // 初始化最小权值为正无穷 int v = -1; // 顶点数组下标 for (int i = 0; i < closeEdges.length; i++) { // 遍历权值数组,找到最小的权值以及对应的顶点数组的下标 if (closeEdges[i].lowCost != 0 && closeEdges[i].lowCost < min) { min = closeEdges[i].lowCost; v = i; } } return v; } // Prim算法构造图G的以u为起始点的最小生成树 public static void Prim(AdjacencyMatrixGraphINF G, Object u) throws Exception{ // 初始化一个二维最小生成树数组minSpanTree,由于最小生成树的边是n-1,所以数组第一个参数是G.getVexNum() - 1,第二个参数表示边的起点和终点符号,所以是2 Object[][] minSpanTree = new Object[G.getVexNum() - 1][2]; int count = 0; // 最小生成树得到的边的序号 // 初始化保存相关顶点和相关顶点间边的权值的数组对象 CloseEdge[] closeEdges = new CloseEdge[G.getVexNum()]; int k = G.locateVex(u); for (int j = 0; j < G.getVexNum(); j++) { if (j!=k) { closeEdges[j] = new CloseEdge(u, G.getArcs()[k][j]);// 将顶点u到其他各个顶点权值写入数组中 } } closeEdges[k] = new CloseEdge(u, 0); // 加入u到自身的权值0 for (int i = 1; i < G.getVexNum(); i++) { // 注意,这里从1开始, k = getMinMum(closeEdges); // 获取u到数组下标为k的顶点的权值最短 minSpanTree[count][0] = closeEdges[k].adjVex; // 最小生成树第一个值为u minSpanTree[count][1] = G.getVexs()[k]; // 最小生成树第二个值为k对应的顶点 count++; closeEdges[k].lowCost = 0; // 下标为k的顶点不参与最小权值的查找了 for (int j = 0; j < G.getVexNum(); j++) { if (G.getArcs()[k][j] < closeEdges[j].lowCost) { closeEdges[j] = new CloseEdge(G.getVex(k), G.getArcs()[k][j]); } } } System.out.print("通过Prim算法得到的最小生成树序列为: {"); for (Object[] Tree : minSpanTree) { System.out.print("(" + Tree[0].toString() + "-" + Tree[1].toString() + ")"); } System.out.println("}"); } }
4.举例说明Prim算法实现过程
以下图为例:

测试类:
// 手动创建一个用于测试最小生成树算法的无向网 public static AdjacencyMatrixGraphINF createUDNByYourHand_ForMiniSpanTree() { Object vexs_UDN[] = {"V0", "V1", "V2", "V3", "V4", "V5", "V6", "V7", "V8"}; int arcsNum_UDN = 15; int[][] arcs_UDN = new int[vexs_UDN.length][vexs_UDN.length]; for (int i = 0; i < vexs_UDN.length; i++) // 构造无向图邻接矩阵 for (int j = 0; j < vexs_UDN.length; j++) if (i==j) { arcs_UDN[i][j]=0; } else { arcs_UDN[i][j] = arcs_UDN[i][j] = INFINITY; } arcs_UDN[0][1] = 10; arcs_UDN[0][5] = 11; arcs_UDN[1][2] = 18; arcs_UDN[1][6] = 16; arcs_UDN[1][8] = 12; arcs_UDN[2][3] = 22; arcs_UDN[2][8] = 8; arcs_UDN[3][4] = 20; arcs_UDN[3][6] = 24; arcs_UDN[3][7] = 16; arcs_UDN[3][8] = 21; arcs_UDN[4][5] = 26; arcs_UDN[4][7] = 7; arcs_UDN[5][6] = 17; arcs_UDN[6][7] = 19; for (int i = 0; i < vexs_UDN.length; i++) // 构造无向图邻接矩阵 for (int j = i; j < vexs_UDN.length; j++) arcs_UDN[j][i] = arcs_UDN[i][j]; return new AdjMatGraph(GraphKind.UDN, vexs_UDN.length, arcsNum_UDN, vexs_UDN, arcs_UDN); } public static void main(String[] args) throws Exception { AdjMatGraph UDN_Graph = (AdjMatGraph) createUDNByYourHand_ForMiniSpanTree(); MiniSpanTree_Prim.Prim(UDN_Graph, "V0"); }
输出为:
通过Prim算法得到的最小生成树序列为: {(V0-V1)(V0-V5)(V1-V8)(V8-V2)(V1-V6)(V6-V7)(V7-V4)(V7-V3)}
分析算法执行过程:

从V0开始: -count为0,k为0,closeEdges数组的
-lowCost为{0 10 INF INF INF 11 INF INF INF},adjVex数组为{V0,V0,V0,V0,V0,V0,V0,V0,V0}
-比较lowCost,于是k为1,adjVex[1]为V0,minSpanTree[0]为(V0,V1),lowCost为{0 0 INF INF INF 11 INF INF INF}
-k为1,与V1的权值行比较,得到新的
-lowCost为:{0 0 18 INF INF 11 16 INF 12},adjVex数组为{V0,V0,V1,V0,V0,V0,V1,V0,V1}
-比较lowCost,于是k为5,adjVex[5]为V0,minSpanTree[1]为(V0,V5),lowCost为{0 0 18 INF INF 0 16 INF 12}
-k为5,与V5的权值行比较,得到新的
-lowCost为{0 0 18 INF 26 0 16 INF 12},adjVex数组为{V0,V0,V1,V0,V5,V0,V1,V0,V1}
-比较lowCost,于是k为8,adjVex[8]为V1,minSpanTree[2]为(V1,V8),lowCost为{0 0 18 INF INF 0 16 INF 0}
...
三、克鲁斯卡尔(Kruskal)算法
1.Kruskal算法描述
Kruskal算法是根据边的权值递增的方式,依次找出权值最小的边建立的最小生成树,并且规定每次新增的边,不能造成生成树有回路,直到找到n-1条边为止。
Kruskal算法的基本思想是:假设图G=(V,{E})是一个具有n个顶点的连通无向网,T=(V,{TE}是图G的最小生成树,其中,V是T的顶点集,TE是T的边集,则构造最小生成树的步骤是:
- T的初始状态为T=(V,{空}),即开始时,最小生成树T是图G的生成零图。
- 将图G中的边按照权值从小到大的顺序依次选取,若选取的边未使生成树T形成回路,则加入TE中,否则舍弃,直至TE中包含了n-1条边为止。
2.Kruskal算法的C语言代码实现

#include "stdio.h" #include "stdlib.h" #include "io.h" #include "math.h" #include "time.h" #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ #define MAXEDGE 20 #define MAXVEX 20 #define INFINITY 65535 typedef struct { int arc[MAXVEX][MAXVEX]; int numVertexes, numEdges; }MGraph; typedef struct { int begin; int end; int weight; }Edge; /* 对边集数组Edge结构的定义 */ /* 构件图 */ void CreateMGraph(MGraph *G) { int i, j; /* printf("请输入边数和顶点数:"); */ G->numEdges=15; G->numVertexes=9; for (i = 0; i < G->numVertexes; i++)/* 初始化图 */ { for ( j = 0; j < G->numVertexes; j++) { if (i==j) G->arc[i][j]=0; else G->arc[i][j] = G->arc[j][i] = INFINITY; } } G->arc[0][1]=10; G->arc[0][5]=11; G->arc[1][2]=18; G->arc[1][8]=12; G->arc[1][6]=16; G->arc[2][8]=8; G->arc[2][3]=22; G->arc[3][8]=21; G->arc[3][6]=24; G->arc[3][7]=16; G->arc[3][4]=20; G->arc[4][7]=7; G->arc[4][5]=26; G->arc[5][6]=17; G->arc[6][7]=19; for(i = 0; i < G->numVertexes; i++) { for(j = i; j < G->numVertexes; j++) { G->arc[j][i] =G->arc[i][j]; } } } /* 交换权值 以及头和尾 */ void Swapn(Edge *edges,int i, int j) { int temp; temp = edges[i].begin; edges[i].begin = edges[j].begin; edges[j].begin = temp; temp = edges[i].end; edges[i].end = edges[j].end; edges[j].end = temp; temp = edges[i].weight; edges[i].weight = edges[j].weight; edges[j].weight = temp; } /* 对权值进行排序 */ void sort(Edge edges[],MGraph *G) { int i, j; for ( i = 0; i < G->numEdges; i++) { for ( j = i + 1; j < G->numEdges; j++) { if (edges[i].weight > edges[j].weight) { Swapn(edges, i, j); } } } printf("权排序之后的为:\n"); for (i = 0; i < G->numEdges; i++) { printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight); } } /* 查找连线顶点的尾部下标 */ int Find(int *parent, int f) { while ( parent[f] > 0) { f = parent[f]; } return f; } /* 生成最小生成树 */ void MiniSpanTree_Kruskal(MGraph G) { int i, j, n, m; int k = 0; int parent[MAXVEX];/* 定义一数组用来判断边与边是否形成环路 */ Edge edges[MAXEDGE];/* 定义边集数组,edge的结构为begin,end,weight,均为整型 */ /* 用来构建边集数组并排序********************* */ for ( i = 0; i < G.numVertexes-1; i++) { for (j = i + 1; j < G.numVertexes; j++) { if (G.arc[i][j]<INFINITY) { edges[k].begin = i; edges[k].end = j; edges[k].weight = G.arc[i][j]; k++; } } } sort(edges, &G); /* ******************************************* */ for (i = 0; i < G.numVertexes; i++) parent[i] = 0; /* 初始化数组值为0 */ printf("打印最小生成树:\n"); for (i = 0; i < G.numEdges; i++) /* 循环每一条边 */ { n = Find(parent,edges[i].begin); m = Find(parent,edges[i].end); if (n != m) /* 假如n与m不等,说明此边没有与现有的生成树形成环路 */ { parent[n] = m; /* 将此边的结尾顶点放入下标为起点的parent中。 */ /* 表示此顶点已经在生成树集合中 */ printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight); } } } int main(void) { MGraph G; CreateMGraph(&G); MiniSpanTree_Kruskal(G); return 0; }
3.Kruskal算法的Java语言代码实现
package bigjun.iplab.adjacencyMatrix; /** * 最小生成树之Kruskal算法 */ public class MiniSpanTree_Kruskal { private final static int INFINITY = Integer.MAX_VALUE; // 表示正无穷 private static class Edge{ int begin; // 边的起点 int weight; // 边的权值 int end; // 边的终点 public Edge(int begin, int weight, int end) { this.begin = begin; this.weight = weight; this.end = end; } } // 交换两条边的各个属性,包括起点,终点和权值 private static void Swap_edges(Edge[] edges, int i, int j) { int temp; temp = edges[i].begin; edges[i].begin = edges[j].begin; edges[j].begin = temp; temp = edges[i].weight; edges[i].weight = edges[j].weight; edges[j].weight = temp; temp = edges[i].end; edges[i].end = edges[j].end; edges[j].end = temp; } // 对边集数组按照权值进行排序 private static void Sorted_Edge(Edge[] edges) { for (int i = 0; i < edges.length; i++) { for (int j = i + 1; j < edges.length; j++) { if (edges[i].weight > edges[j].weight) { Swap_edges(edges, i, j); } } } } // 查找顶点的尾部下标 private static int Find_indexOfParent(int[] parent, int f) { while (parent[f] > 0) { f = parent[f]; } return f; } public static void Kruskal(AdjacencyMatrixGraphINF G) throws Exception { Edge[] edges = new Edge[G.getArcNum()]; // 定义边集数组 int[] parent = new int[G.getVexNum()]; // 定义一组数组用来判断边与边是否形成回路 int k = 0; for (int i = 0; i < G.getVexNum() - 1; i++) { // 将邻接矩阵G转化为边集数组edges for (int j = i + 1; j < G.getVexNum(); j++) { if (G.getArcs()[i][j] < INFINITY) { edges[k] = new Edge(i, G.getArcs()[i][j], j); k++; } } } Sorted_Edge(edges); // 对边集数组按照权值从小到大排序 for (int i = 0; i < G.getVexNum(); i++) { // 初始化判断边与边是否形成回路数组 parent[i] = 0; } System.out.print("通过Kruskal算法得到的最小生成树序列为: {"); for (int i = 0; i < edges.length; i++) { // 遍历每一条边 int n = Find_indexOfParent(parent, edges[i].begin); int m = Find_indexOfParent(parent, edges[i].end); if (n!=m) { // 如果不构成回路的话 parent[n] = m; // 将此边的结尾项放在下标为起点的parent中,表示此顶点已经在生成树集合中 System.out.print("(" + G.getVex(edges[i].begin) + "-" + G.getVex(edges[i].end) + ")"); } } System.out.println("}"); } }
4.Kruskal算法的距离说明实现过程
以下图为例:
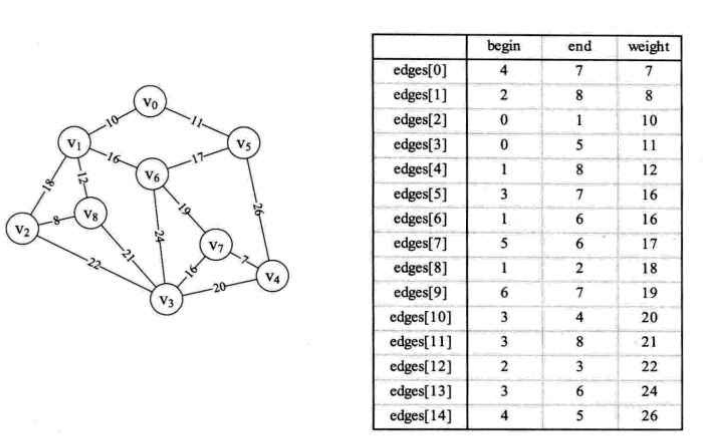
测试代码:
// 手动创建一个用于测试最小生成树算法的无向网 public static AdjacencyMatrixGraphINF createUDNByYourHand_ForMiniSpanTree() { Object vexs_UDN[] = {"V0", "V1", "V2", "V3", "V4", "V5", "V6", "V7", "V8"}; int arcsNum_UDN = 15; int[][] arcs_UDN = new int[vexs_UDN.length][vexs_UDN.length]; for (int i = 0; i < vexs_UDN.length; i++) // 构造无向图邻接矩阵 for (int j = 0; j < vexs_UDN.length; j++) if (i==j) { arcs_UDN[i][j]=0; } else { arcs_UDN[i][j] = arcs_UDN[i][j] = INFINITY; } arcs_UDN[0][1] = 10; arcs_UDN[0][5] = 11; arcs_UDN[1][2] = 18; arcs_UDN[1][6] = 16; arcs_UDN[1][8] = 12; arcs_UDN[2][3] = 22; arcs_UDN[2][8] = 8; arcs_UDN[3][4] = 20; arcs_UDN[3][6] = 24; arcs_UDN[3][7] = 16; arcs_UDN[3][8] = 21; arcs_UDN[4][5] = 26; arcs_UDN[4][7] = 7; arcs_UDN[5][6] = 17; arcs_UDN[6][7] = 19; for (int i = 0; i < vexs_UDN.length; i++) // 构造无向图邻接矩阵 for (int j = i; j < vexs_UDN.length; j++) arcs_UDN[j][i] = arcs_UDN[i][j]; return new AdjMatGraph(GraphKind.UDN, vexs_UDN.length, arcsNum_UDN, vexs_UDN, arcs_UDN); } public static void main(String[] args) throws Exception { AdjMatGraph UDN_Graph = (AdjMatGraph) createUDNByYourHand_ForMiniSpanTree(); MiniSpanTree_Prim.Prim(UDN_Graph, "V0"); MiniSpanTree_Kruskal.Kruskal(UDN_Graph); }
输出为:
通过Kruskal算法得到的最小生成树序列为: {(V4-V7)(V2-V8)(V0-V1)(V0-V5)(V1-V8)(V3-V7)(V1-V6)(V6-V7)}
分析算法执行过程(重点分析如何利用parent数组来判断新加入的边是否构成回路):

i=0,parent[]={0,0,0,0,0,0,0,0,0},edge[0].begin=4,edge[0].end=7,n=4,m=7,parent[4]=7,打印(V4,V7)
i=1,parent[]={0,0,0,0,7,0,0,0,0},edge[1].begin=2,edge[1].end=8,n=2,m=8,parent[2]=8,打印(V2,V8)
i=2,parent[]={0,0,8,0,7,0,0,0,0},edge[2].begin=0,edge[2].end=1,n=0,m=1,parent[0]=1,打印(V0,V1)
i=3,parent[]={1,0,8,0,7,0,0,0,0},edge[3].begin=0,edge[3].end=5,n=1,m=5,parent[1]=5,打印(V0,V5)
i=4,parent[]={1,5,8,0,7,0,0,0,0},edge[4].begin=1,edge[4].end=8,n=5,m=8,parent[5]=8,打印(V1,V8)
i=5,parent[]={1,5,8,0,7,8,0,0,0},edge[5].begin=3,edge[5].end=7,n=3,m=7,parent[3]=7,打印(V3,V7)
i=6,parent[]={1,5,8,7,7,8,0,0,0},edge[6].begin=1,edge[6].end=6,n=8,m=6,parent[8]=6,打印(V1,V6)
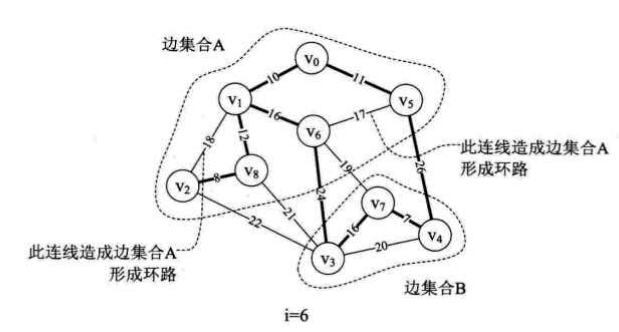
i=6时,parent[]={1,5,8,7,7,8,0,0,6},如上右图,有两个连通的边集合A与B共同被纳入到最小生成树中,其中,对于集合A来说,
parent[0]=1表示V0和V1已经在生成树的边集合A中,
parent[1]=5表示V1和V5也在边集合A中,
同理parent[5]=8表示V5和V8在边集合A中,parent[8]=6表示V8和V6在边集合A中
此时,parent[6]=0表示集合A暂时到头,所以要重点关注的就是parent[6]的值
同理,边集合B中,parent[3]=7,parent[4]=7,parent[7]=0,表示V3、V4、V7在另一个边集合B中并且暂时到头,所以要重点关注的就是parent[7]的值
i=7时,parent[]={1,5,8,7,7,8,0,0,6},edge[7].begin=5,edge[7].end=6, parent[5]=8,parent[8]=6,parent[6]=0,即n=6,而parent[6]=0即m=7,
此时n=m=6,所以不能打印,实际上也就是如果parent[6]=6就表示V6到V6,这就是环路了!另一方面,直观来看(V5,V6)这条边加上去之后会构成环路,所以就不行。跳出循环。
i=8,同理
i=9,parent[]={1,5,8,7,7,8,0,0,6,edge[9].begin=6,edge[9].end=7,n=6,m=7,parent[6]=7,打印(V6,V7)
i=10~14,同理。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号