数据结构（三十）图的邻接矩阵存储结构

　　一、邻接矩阵的Java语言代码实现：

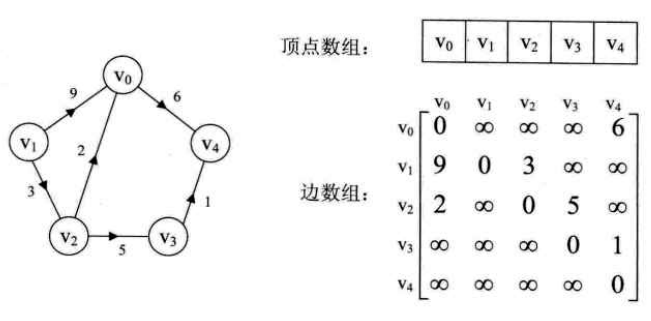
　　以有向网为例，无向网中矩阵对称，而有向图和无向图原理类似，只是把正无穷换成0，有连接的地方为1即可：

　　

• 类的四种类型枚举类

package bigjun.iplab.adjacencyMatrix;
/**
 * 图的四种主要类型的枚举类
 */
public enum GraphKind {

    UDG,    // 无向图
    DG,        // 有向图
    UDN,    // 无向网
    DN,        // 有向网
}

• 接口类

package bigjun.iplab.adjacencyMatrix;
/**
 * 图的邻接矩阵存储结构接口类
 */
public interface AdjacencyMatrixGraphINF {
    
    // 创建一个图
    public void createGraph();
    // 返回图中的顶点数
    public int getVexNum();
    // 返回图中的边数
    public int getArcNum();
    // 给定顶点的位置v，返回其对应的顶点值
    public Object getVex(int x) throws Exception;
    // 给定顶点的值vex，返回其在图中的位置
    public int locateVex(Object vex);
    // 返回顶点v的第一个邻接点
    public int firstAdjvex(int v) throws Exception;
    // 返回v相对于w的下一个邻接点
    public int nextAdjvex(int v, int w) throws Exception;
    
}

• 实现类：

package bigjun.iplab.adjacencyMatrix;

import java.util.Scanner;

public class AdjMatGraph implements AdjacencyMatrixGraphINF{
    
    private final static int INFINITY = Integer.MAX_VALUE;    // 表示正无穷
    private GraphKind kind;            // 图的种类标志
    private int vexNum, arcNum;        // 顶点数，边数
    private Object[] vexs;            // 顶点一维数组
    private int[][] arcs;            // 邻接矩阵
    
    // 构造方法1: 构造一个空图
    public AdjMatGraph() {
        this(null, 0, 0, null, null);
    }
    
    // 构造方法2: 构造一个非空图
    public AdjMatGraph(GraphKind kind, int vexNum, int arcNum, Object[] vexs, int[][] arcs) {
        this.kind = kind;
        this.vexNum = vexNum;
        this.arcNum = arcNum;
        this.vexs = vexs;
        this.arcs = arcs;
    }

    // 创建图的四种类型中的一种
    public void createGraph() {
        @SuppressWarnings("resource")
        Scanner scanner = new Scanner(System.in);
        System.out.println("请输入图的类型代号(UDG(无向图)、DG(有向图)、UDN(无向网)、DN(有向网)):");
        GraphKind kind = GraphKind.valueOf(scanner.next());
        switch (kind) {
        case UDG:
            createUnDirecedGraph();
            return;
        case DG:
            createDirectedGraph();
            return;
        case UDN:
            createUnDirectedNet();
            return;
        case DN:
            createDirectedNet();
            return;
        }
        System.out.println("图已创建完成！");
    }
    
    // 创建无向图
    private void createUnDirecedGraph() {
        @SuppressWarnings("resource")
        Scanner sc = new Scanner(System.in);
        System.out.println("请分别输入图的顶点数，图的边数: ");
        vexNum = sc.nextInt();
        arcNum = sc.nextInt();
        vexs = new Object[vexNum];
        System.out.println("请分别输入图的各个顶点: ");
        for (int i = 0; i < vexNum; i++) {                // 初始化顶点一维数组
            vexs[i] = sc.next();
        }
        arcs = new int[vexNum][vexNum];
        for (int v = 0; v < vexNum; v++) {                // 初始化邻接矩阵，在每个位置都放上0
            for (int u = 0; u < vexNum; u++) {
                arcs[v][u] = 0;                            
            }
        }
        System.out.println("请输入各个边的两个顶点: ");
        for (int k = 0; k < arcNum; k++) {                // 填入对应位置上的1
            int v = locateVex(sc.next());
            int u = locateVex(sc.next());
            arcs[v][u] = arcs[u][v] = 1;        
        }
    }
    
    // 创建有向图
    private void createDirectedGraph() {
        @SuppressWarnings("resource")
        Scanner sc = new Scanner(System.in);
        System.out.println("请分别输入图的顶点数，图的边数: ");
        vexNum = sc.nextInt();
        arcNum = sc.nextInt();
        vexs = new Object[vexNum];
        System.out.println("请分别输入图的各个顶点: ");
        for (int i = 0; i < vexNum; i++) {                // 初始化顶点一维数组
            vexs[i] = sc.next();
        }
        arcs = new int[vexNum][vexNum];
        for (int v = 0; v < vexNum; v++) {                // 初始化邻接矩阵，在每个位置都放上0
            for (int u = 0; u < vexNum; u++) {
                arcs[v][u] = 0;
            }
        }
        System.out.println("请输入各个边的两个顶点: ");
        for (int k = 0; k < arcNum; k++) {                // 填入对应的权值
            int v = locateVex(sc.next());
            int u = locateVex(sc.next());
            arcs[v][u] = 1;                                
        }
    }
    
    // 创建无向网
    private void createUnDirectedNet() {
        @SuppressWarnings("resource")
        Scanner sc = new Scanner(System.in);
        System.out.println("请分别输入图的顶点数，图的边数: ");
        vexNum = sc.nextInt();
        arcNum = sc.nextInt();
        vexs = new Object[vexNum];
        System.out.println("请分别输入图的各个顶点: ");
        for (int i = 0; i < vexNum; i++) {                // 初始化顶点一维数组
            vexs[i] = sc.next();
        }
        arcs = new int[vexNum][vexNum];
        for (int v = 0; v < vexNum; v++) {                // 初始化邻接矩阵，在每个位置都放上正无穷
            for (int u = 0; u < vexNum; u++) {
                arcs[v][u] = INFINITY;
                arcs[u][u] = 0;
            }
        }
        System.out.println("请输入各个边的两个顶点及其权值: ");
        for (int k = 0; k < arcNum; k++) {                // 填入对应的权值
            int v = locateVex(sc.next());
            int u = locateVex(sc.next());
            arcs[v][u] = arcs[u][v] = sc.nextInt();        // 由于无向网是矩阵对称的，所以在对称的位置填上对应的值
        }
    }
    
    // 创建有向网
    private void createDirectedNet() {
        @SuppressWarnings("resource")
        Scanner sc = new Scanner(System.in);
        System.out.println("请分别输入图的顶点数，图的边数: ");
        vexNum = sc.nextInt();
        arcNum = sc.nextInt();
        vexs = new Object[vexNum];
        System.out.println("请分别输入图的各个顶点: ");
        for (int i = 0; i < vexNum; i++) {                // 初始化顶点一维数组
            vexs[i] = sc.next();
        }
        arcs = new int[vexNum][vexNum];
        for (int v = 0; v < vexNum; v++) {                // 初始化邻接矩阵，在每个位置都放上正无穷
            for (int u = 0; u < vexNum; u++) {
                arcs[v][u] = INFINITY;
                arcs[u][u] = 0;
            }
        }
        System.out.println("请输入各个边的两个顶点及其权值: ");
        for (int k = 0; k < arcNum; k++) {                // 填入对应的权值
            int v = locateVex(sc.next());
            int u = locateVex(sc.next());
            arcs[v][u] = sc.nextInt();                    // 有向网不对称
        }
    }

    // 返回顶点数
    public int getVexNum() {
        return vexNum;
    }

    // 返回边数
    public int getArcNum() {
        return arcNum;
    }

    // 返回v表示结点的值
    public Object getVex(int x) throws Exception{
        if (x < 0 && x >= vexNum ) 
            throw new Exception("给定的顶点不存在");
        return vexs[x];
    }

    // 返回顶点的值为vex的顶点在顶点数组的位置下标，如果图中不包含值为vex的顶点，则返回-1
    public int locateVex(Object vex) {
        for (int v = 0; v < vexNum; v++) {
            if (vexs[v].equals(vex)) {
                return v;
            }
        }
        return -1;
    }

    // 返回下标为v的顶点的第一个邻接点，即遍历邻接矩阵的第v行,找到之后，返回第v行对应的下标
    public int firstAdjvex(int v) throws Exception {
        if (v < 0 && v >= vexNum ) 
            throw new Exception("给定的顶点不存在");
        for (int j = 0; j < vexNum; j++) {
            if (arcs[v][j] != 0 && arcs[v][j] < INFINITY) {
                return j;
            }
        }
        return -1;
    }

    // 返回下标为v的顶点相对于下标为w的顶点的下一个邻接点，若w是v的最后一个邻接点，则返回-1
    public int nextAdjvex(int v, int w) throws Exception {
        if (v < 0 && v >= vexNum ) 
            throw new Exception("给定的顶点不存在");
        for (int j = w + 1; j < vexNum; j++) {
            if (arcs[v][j] != 0 && arcs[v][j] < INFINITY) {
                return j;
            }
        }
        return -1;
    }    

    public static void main(String[] args) throws Exception {
        AdjMatGraph aMatGraph = new AdjMatGraph();
        aMatGraph.createGraph();
        System.out.println("该类型的图已经创建完成！");
        System.out.println("顶点2的第一个邻接点是: " + aMatGraph.firstAdjvex(2));
        System.out.println("顶点2的相对于顶点0的下一个邻接点是: " + aMatGraph.nextAdjvex(2, 0));
    }
}

• 输出：

请输入图的类型代号(UDG(无向图)、DG(有向图)、UDN(无向网)、DN(有向网)):
DN
请分别输入图的顶点数，图的边数: 
5 6
请分别输入图的各个顶点: 
0 1 2 3 4
请输入各个边的两个顶点及其权值: 
2 0 2
1 0 9
1 2 3
2 3 5
3 4 1
0 4 6
该类型的图已经创建完成！
顶点2的第一个邻接点是: 0
顶点2的相对于顶点0的下一个邻接点是: 3

　　

　　二、邻接矩阵的创建C语言代码实现：

#include "stdio.h"    
#include "stdlib.h"   
#include "io.h"  
#include "math.h"  
#include "time.h"

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXVEX 100 /* 最大顶点数，应由用户定义 */
#define INFINITY 65535

typedef int Status;    /* Status是函数的类型,其值是函数结果状态代码，如OK等 */
typedef char VertexType; /* 顶点类型应由用户定义  */
typedef int EdgeType; /* 边上的权值类型应由用户定义 */
typedef struct
{
    VertexType vexs[MAXVEX]; /* 顶点表 */
    EdgeType arc[MAXVEX][MAXVEX];/* 邻接矩阵，可看作边表 */
    int numNodes, numEdges; /* 图中当前的顶点数和边数  */
}MGraph;

/* 建立无向网图的邻接矩阵表示 */
void CreateMGraph(MGraph *G)
{
    int i,j,k,w;
    printf("输入顶点数和边数:\n");
    scanf("%d,%d",&G->numNodes,&G->numEdges); /* 输入顶点数和边数 */
    for(i = 0;i <G->numNodes;i++) /* 读入顶点信息,建立顶点表 */
        scanf(&G->vexs[i]);
    for(i = 0;i <G->numNodes;i++)
        for(j = 0;j <G->numNodes;j++)
            G->arc[i][j]=INFINITY;    /* 邻接矩阵初始化 */
    for(k = 0;k <G->numEdges;k++) /* 读入numEdges条边，建立邻接矩阵 */
    {
        printf("输入边(vi,vj)上的下标i，下标j和权w:\n");
        scanf("%d,%d,%d",&i,&j,&w); /* 输入边(vi,vj)上的权w */
        G->arc[i][j]=w; 
        G->arc[j][i]= G->arc[i][j]; /* 因为是无向图，矩阵对称 */
    }
}

int main(void)
{    
    MGraph G;    
    CreateMGraph(&G);
    
    return 0;
}