数据结构(二十六)树、森林与二叉树的转换
一、树、森林与二叉树转换的意义
二叉树由于每个结点最多只能有左孩子和右孩子,而在树中一个结点可以包括任意数目的子结点,因此二叉树的很多性质和算法被研究了出来。如果所有的树都向二叉树一样方便就好了。树与二叉树、森林与二叉树之间可以相互转换,而且这种转换是一一对应的。
二、树转换为二叉树
为了操作方便,假设树是一棵有序树,也就是说将树中每一个结点的孩子按从左到右的顺序进行编号,
将树转换为二叉树的步骤为:
- 加线:将树中所有相邻的兄弟之间加一条连线。
- 去线:将树中的每一个结点,只保留它与第1个孩子结点之间的连线,删去它与其他孩子结点之间的连线。
- 旋转:以树的根结点为轴心,将整棵树顺时针旋转一定的角度并做适当的调整,使之结构分明。
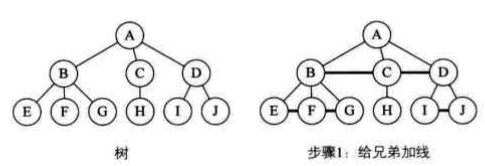
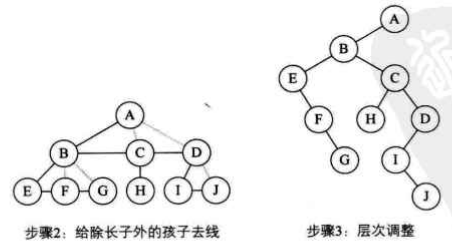
由转换过程可知,树与由它转换成的二叉树是一一对应的,树中的任意一个结点都对应着二叉树中的每一个结点,树中每一个结点的第1个孩子结点在二叉树中是对应结点的左孩子,而树中每一结点的右邻兄弟在二叉树中是对应结点的右孩子(E的右邻兄弟是F,所以F是E的右孩子;F的右邻兄弟是G,所以G是F的右孩子)。也就是说,在二叉树中,左分支上的每个结点在原来的树中是父子关系,而右分支上的各个结点在原来的树中是兄弟关系。由于树中的根结点没有兄弟,所以由树转换成的二叉树永远都是一颗根结点的右子树为空的二叉树。
三、二叉树转换为树
二叉树转换为树是树转换为二叉树的逆过程,具体步骤为:
- 加线:若某结点是其双亲结点的左孩子,则将该结点沿着右分支向下的所有结点(该结点的右孩子结点,右孩子结点的右孩子结点,...)与该结点的双亲结点用线连接。
- 删线:将树中所有双亲结点与右孩子结点的连线删除。
- 旋转:以树的根结点为轴心,将整棵树逆时针旋转一定的角度并做适当的调整,使之结构分明。
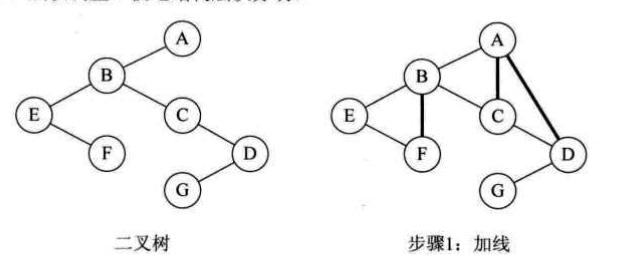
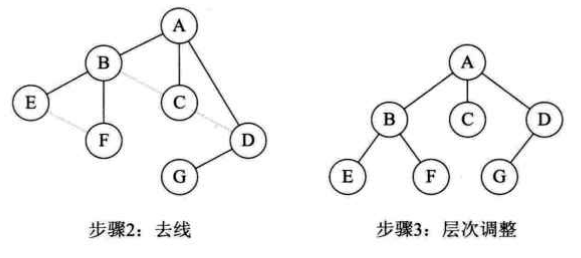
四、森林转换为二叉树
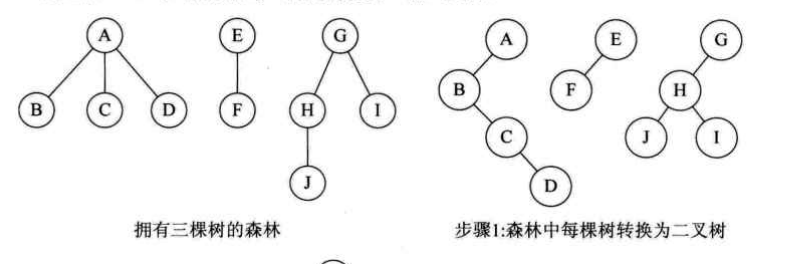
森林是若干棵树的集合,而任何一颗和树对应的二叉树的右子树一定为空,则可以得到将森林转换为二叉树的步骤为:
- 把每棵树转换为二叉树
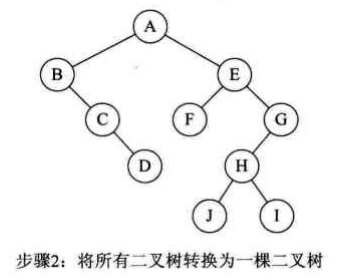
- 按照森林中树的先后顺序,将后一棵二叉树视为前一棵二叉树的右子树依次连接,从而构成一颗二叉树
五、二叉树转换为森林
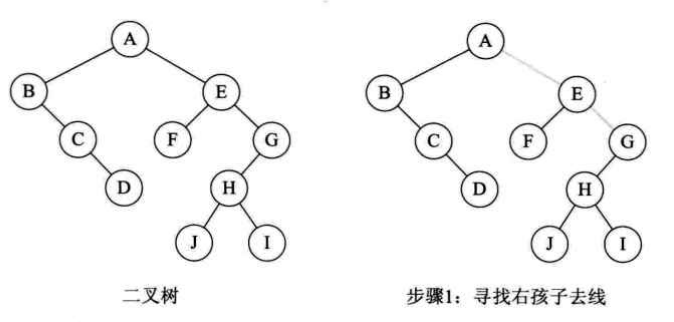
判断一颗二叉树能够转换成一颗树还是森林,只要看这棵二叉树的根结点有没有右孩子,如果有右孩子就是森林,没有右孩子就是一棵树。二叉树转换为森林的步骤为:
- 从根结点开始,若右孩子存在,则把右孩子结点的连线删除,再查看分离后的二叉树,若右孩子存在,则把右孩子结点的连线删除...直到所有右孩子连线都删除为止
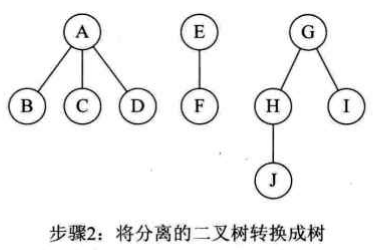
- 将每棵分离后的二叉树转换为树
六、树的遍历
树可以被看成由树的根结点和根结点的所有子树所构成的森林两部分构成,因此树的遍历操作主要有前序遍历、后序遍历和层次遍历三种方式。
1.前序遍历:
若树为非空,则
- 访问根结点
- 从左到右依次先序遍历根结点的每一棵子树
2.后序遍历
若树为非空,则
- 从左到右依次后序遍历根结点的每一棵子树
- 访问根结点
3.层次遍历
若树为非空,则
- 从上到下依次访问每一层的各个结点,在同一层中的结点,则按从左到右的顺序依次进行访问(使用队列实现)。


- 前序遍历:ABEFCDG
- 后序遍历:EFBCGDA
- 层次遍历:ABCDEFG
七、森林的遍历
森林也可以看成是由第一棵树的根结点、第一棵树的根结点的子树所构成的森林和除第一棵树之外的其余树所构成的森林三部分构成。
1.前序遍历
若森林为非空,则
- 访问森林中第一棵树的根结点
- 前序遍历第一棵树中根结点的子树所构成的森林
- 前序遍历森林中除第一棵树之外的其他树所构成的森林
2.后序遍历
若森林为非空,则
- 后序遍历第一棵树中根结点的子树所构成的森林
- 访问森林中第一棵树的根结点
- 后序遍历森林中除第一棵树之外的其他树所构成的森林
3.层次遍历
若森林为非空,则
- 按从左到右的顺序对森林中的每一棵树进行层次遍历


- 前序遍历:ABCDEFGHJI
- 后序遍历:BCDAFEJHIG
- 层次遍历:ABCDEFGHIJ




