数据结构(二十二)二叉树遍历算法的应用与二叉树的建立
一、二叉树遍历算法的应用
1.二叉树的查找:在以T为根结点的二叉树中查找值为x的结点,若找到,则返回该结点;否则,返回空值。
(1)主要思想:可在二叉树的先序遍历过程中进行,并且在遍历时将访问根结点的操作视为是将根结点的值与x进行比较的操作。
复习一下二叉树的先序递归遍历的实现为:
// 先序递归遍历算法 public void preOrderTraverse(BiTreeNode T) { if (T != null) { System.out.print(T.data); preOrderTraverse(T.lchild); preOrderTraverse(T.rchild); } }
(2)主要操作步骤:
- 若二叉树为空;则不存在这个结点,返回控制;否则,将根结点的值与x进行比较,若相等,则返回该结点
- 若根结点的值与x不相等,则在左子树中进行查找,若找到,则返回找到的结点
- 若在左子树中没找到值为x的结点,则继续在右子树中进行查找,并返回查找结果
(3)代码实现
// (先序递归遍历算法)在二叉树中查找值为x的结点,若找到,则返回该结点;否则,返回null public BiTreeNode searchBTNode(BiTreeNode T, Object x) { if (T != null) { if (T.data == x) { // 判断根结点 return T;// 注意这里的return语句,只要查找到了就不用再继续往下查找了,不同于先序递归遍历算法要遍历完全部结点才结束。 } else { // 查找左子树 BiTreeNode lResult = searchBTNode(T.lchild, x); // 若在左子树中查找到x的结点,则返回该结点;否则,查找右子树并返回结果 return lResult != null ? lResult : searchBTNode(T.rchild, x); } } return null; }
2.二叉树中结点的个数统计:返回二叉树中结点的个数
(1)主要思想:二叉树中结点的个数等于1个根结点再分别加上它的左、右子树中结点的个数,同样可以以先序遍历为基础。在二叉树的先序遍历递归算法中,引入一个计数变量count,count初值设定为0;将访问根结点的操作视为对count加1的操作,同时,将每一个对结点的访问打印都执行count加1操作
复习一下二叉树的先序递归遍历的实现为:
// 先序递归遍历算法 public void preOrderTraverse(BiTreeNode T) { if (T != null) { System.out.print(T.data); preOrderTraverse(T.lchild); preOrderTraverse(T.rchild); } }
(2)主要操作过程:
- count赋初值为0
- 若二叉树非空,则:①count值加1;②统计根结点的左子树的结点个数,并加入到count变量中;③统计根结点的右子树的结点个数,并加入到count变量中;
- 返回count值
(3)代码实现:
// (先序递归遍历算法)统计二叉树中结点的个数并返回 public int countBTNode(BiTreeNode T) { int count = 0; if (T != null) { ++count; count += countBTNode(T.lchild); count += countBTNode(T.rchild); } return count; }
3.求二叉树的深度:求二叉树的深度并返回
(1)主要思想;二叉树的深度就是左子树的深度和右子树的深度中的最大值加1。这个时候,很自然就想到使用后序遍历的递归算法,因为后序遍历最后访问根结点。
复习一下后序遍历递归算法的实现为:
// 后序递归遍历算法 public void postOrderTraverse(BiTreeNode T) { if (T != null) { postOrderTraverse(T.lchild); postOrderTraverse(T.rchild); System.out.print(T.data); } }
(2)主要操作步骤:
- 若二叉树为空,则返回0,否则:①求左子树的深度;②求右子树的深度;③将左、右子树深度的最大值加1并返回
(3)代码实现:
// (后序递归遍历算法)求二叉树的深度 public int getBTDepth(BiTreeNode T) { if (T != null) { int lDepth = getBTDepth(T.lchild); int rDepth = getBTDepth(T.rchild); return 1 + (lDepth > rDepth ? lDepth : rDepth); } return 0; }
4.判断两棵二叉树是否相等:若相等,则返回true;否则,返回false
(1)主要思想:两棵二叉树相等只有两种情况:①两棵二叉树都为空;②两棵二叉树的根结点、左子树和右子树分别对应相等。判断结点是否相等只用判断结点的数据域是否相等即可,因此,可以使用先序遍历的思路来判断两棵二叉树的结点是否相等。
复习一下先序遍历递归算法的实现为:
// 先序递归遍历算法 public void preOrderTraverse(BiTreeNode T) { if (T != null) { System.out.print(T.data); preOrderTraverse(T.lchild); preOrderTraverse(T.rchild); } }
(2)主要操作步骤:
- 若两棵二叉树都为空,则它们相等,返回true;
- 若两棵二叉树都非空,则:①若根结点的值相等,则继续判断它们的左子树是否相等;②若左子树相等,则继续判断它们的右子树是否相等;③若右子树也相等,则这两棵二叉树相等,返回true
- 其他任何情况都返回false
(3)代码实现
// (先序递归遍历算法) 判断两棵二叉树是否相等,若相等,返回true;否则,返回false public boolean isEqual(BiTreeNode T1, BiTreeNode T2) { if (T1 == null && T2 == null) return true; if (T1 != null && T2 != null) { if (T1.data.equals(T2.data)) { if (isEqual(T1.lchild, T2.lchild)) { if (isEqual(T1.rchild, T2.rchild)) { return true; } } } } return false; }
二、二叉树的建立
首先复习一下二叉树遍历的性质:前序遍历或后序遍历序列能反应双亲与孩子结点之间的层次关系,而中序遍历序列能反应兄弟结点之间的左右次序关系。所以,仅仅已知一种二叉树的遍历序列是不能唯一确定一棵二叉树的。只有以下两种情况:
- 已知前序遍历序列和中序遍历序列,可以唯一确定一棵二叉树。
- 已知后序遍历序列和中序遍历序列,可以唯一确定一棵二叉树。
1.由前序和中序遍历序列建立一棵二叉树
(1)主要思想:由于二叉树是具有层次关系的结点所构成的非线性结构,而且二叉树中的每个结点的两棵子树具有左、右次序之分,所以要建立一棵二叉树,就必须明确的是:结点与双亲结点和孩子结点之间的层次关系;兄弟结点的左右次序关系。而根据前序和中序遍历序列就能确定结点之间的这两种关系。
(2)主要操作步骤:
- 取前序遍历序列中的第一个结点作为根结点;
- 在中序遍历序列中寻找根结点,确定根结点再中序遍历序列中的位置,假设为i(0<=i<=count-1),其中count为二叉树遍历序列中结点的个数;
- 在中序遍历中确定:根结点之前的i个结点序列构成左子树的中序遍历序列,根结点之后的count-i-1个结点序列构成右子树的中序遍历序列;
- 在先序遍历序列中确定:根结点之后i个结点序列构成左子树的先序遍历序列,剩下的count-i-1个结点序列构成右子树的先序遍历序列;
- 用第3步和第4步,确定左、右子树的根结点,通过递归就可以建立唯一的一棵二叉树。
(3)代码实现
1 // 构造方法3:由前序遍历序列和中序遍历序列建立一棵二叉树 2 public LinkBiTree(String preOrder, String inOrder, int preIndex, int inIndex, int count) { 3 // 如果前序和中序遍历序列不为空 4 if (count > 0) { 5 // 取前序遍历序列的第一个结点作为根结点 6 char rChar = preOrder.charAt(preIndex); 7 int i = 0; 8 // 确定根结点在中序遍历序列的第i(从0开始)个位置 9 for ( ; i < count; i++) { 10 if (rChar == inOrder.charAt(i + inIndex)) { 11 break; 12 } 13 } 14 // 创建根结点对应的二叉树链式存储结构的结点 15 root = new BiTreeNode(rChar); 16 // 确定左子树的根结点 17 root.lchild = new LinkBiTree(preOrder, inOrder, preIndex + 1, inIndex, i).root; 18 // 确定右子树的根结点 19 root.rchild = new LinkBiTree(preOrder, inOrder, preIndex + i + 1, inIndex + i + 1, count - i - 1).root; 20 } 21 }
以 String preOrder = "ABDHKECFIGJ";
String inOrder = "HKDBEAIFCGJ";
LinkBiTree biTreeByPreAndIn = new LinkBiTree(preOrder, inOrder, 0, 0, preOrder.length());分析实现过程:
实现过程为:
-cuont值为11-根结点为A-中序遍历中i=5的位置是根结点-创建A-
-进入17创建A的左孩子:count为5,根结点为B,中序遍历中i=4的位置是根结点-创建B
-进入17创建B的左孩子:count为4,根结点为D,中序遍历中i=3的位置是根结点-创建D
-进入17创建D的左孩子:count为3,根结点为H,中序遍历中i=0的位置是根结点-创建H
-进入17创建H的左孩子:count为0,跳出,进入18创建H的右孩子,..
2.由中序和后序遍历序列建立一棵二叉树
(1)主要思想和由前序和中序遍历序列建立一棵二叉树一致。
(2)按照之前的思路可以设计主要的操作步骤
- 取后序遍历序列中的最后一个结点作为根结点;
- 在中序遍历序列中寻找根结点,确定根结点再中序遍历序列中的位置,假设为i(0<=i<=count-1),其中count为二叉树遍历序列中结点的个数;
- 在中序遍历中确定:根结点之前的i个结点序列构成左子树的中序遍历徐磊,根结点之后的count-i-1个结点序列构成右子树的中序遍历序列;
- 在后序遍历序列中确定:0到i-1个结点序列构成左子树的后序遍历序列,i到count-2个结点序列构成右子树的后序遍历序列;
- 用第3步和第4步,确定左、右子树的根结点,通过递归就可以建立唯一的一棵二叉树。
3.由标明空子树的前序遍历序列建立一棵二叉树
(1)已知二叉树的前序遍历序列是不能唯一确定一棵二叉树的,如果能够在前序遍历序列中接入每一个结点的空子树信息,则可以明确二叉树中结点与双亲、孩子与兄弟间的关系,因此就可以唯一确定一棵二叉树。例如,以下面的二叉树为例:
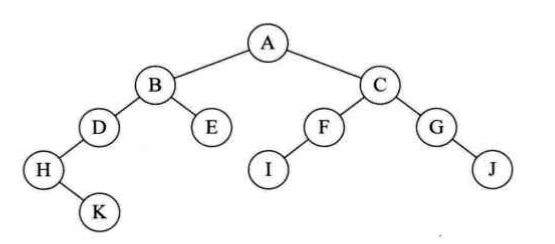
标明空子树“#”的前序遍历序列为:ABDH#K###E##CFI###G#J##
(2)主要操作步骤:
- 从标明空子树信息的前序遍历序列中依次读入字符,若读入的字符是“#”,则建立空树;否则
- 建立根结点
- 继续建立树的左子树
- 继续建立树的右子树
(3)代码实现
// 构造方法4:由标明空子树的前序遍历序列建立一棵二叉树 // static修饰的变量叫静态变量或类变量,JVM只分配一次内存,在对象之间共享值时要用static修饰 private static int index = 0;// 这里要注意的是index要加staic关键字,否则每次new LinkBiTree(preStr)出新对象的时候index都是0,那样就会陷入死递归 public LinkBiTree(String preStr) { char c = preStr.charAt(index++); if (c != '#') { root = new BiTreeNode(c); root.lchild = new LinkBiTree(preStr).root; root.rchild = new LinkBiTree(preStr).root; } else root = null; }
4.由完全二叉树的顺序存储结构建立其二叉树链式存储结构
(1)主要思想:根据二叉树的性质5:完全二叉树中编号为i的结点其左、右孩子的编号分别为2i+1、2i+2(根结点编号为0)
(2)代码实现:
//由顺序存储的完全二叉树建立一棵连式存储的二叉树结点 public BiTreeNode createBiTreeNodeBySeqBiTree(String seqBiTree, int index) { BiTreeNode root = null; // 根结点 if (index < seqBiTree.length()) { // 位置不超过字符串长度 root = new BiTreeNode(seqBiTree.charAt(index)); // 从下标为0开始,建立二叉链表根结点 root.lchild = createBiTreeNodeBySeqBiTree(seqBiTree, 2 * index + 1);// 建立左子树 root.rchild = createBiTreeNodeBySeqBiTree(seqBiTree, 2 * index + 2);// 建立右子树 } return root; // 返回二叉链表根结点对象 } // 由顺序存储的完全二叉树建立一棵连式存储的二叉树 public LinkBiTree createBiTreeBySeqBiTree(String seqBiTree, int index) { BiTreeNode root = createBiTreeNodeBySeqBiTree(seqBiTree, index); return new LinkBiTree(root); }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号