最大子数组问题
1. 问题描述
对于数组(如下),求解其最大子数组.

结果为: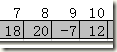
2. 算法设计
采用递归的方法求解
A. 求解数组左半部分的最大子数组
B. 求解数组右半部分的最大子数组
C. 求解整个数组的最大子数组
D. 比较A,B,C求出的结果,选出一个最大值,即为最终结果.
3. 数据结构设计
A. 中间结果的三元组,(子数组下标,子数组上标,子数组和)
1 class Tuple 2 { 3 public: 4 int low, high, sum; 5 Tuple(int l = 0, int h = 0, int s = 0):low(l), high(h), sum(s) { } 6 };
B. 数组元素
1 std::vector<int> m_array;
4. 算法实现
算法实现文件: calc_max_subarray.h
1 #include <iostream> 2 #include <vector> 3 #include <cassert> 4 #include <fstream> 5 6 using namespace std; 7 8 namespace nsp_subarray 9 { 10 class Tuple 11 { 12 public: 13 int low, high, sum; 14 Tuple(int l = 0, int h = 0, int s = 0):low(l), high(h), sum(s) { } 15 }; 16 17 class SubArray 18 { 19 private: 20 std::vector<int> m_array; 21 public: 22 SubArray() { m_array.clear(); } 23 24 virtual ~SubArray(){} 25 26 void init_data(string fileName) 27 { 28 ifstream in(fileName.c_str()); 29 while(!in.eof()) 30 { 31 int e = 0; 32 in >> e; 33 m_array.push_back(e); 34 } 35 } 36 37 inline int get_array_size() { return m_array.size(); } 38 39 Tuple find_max_crossing_subarray(int low, int mid, int high) 40 { 41 int m_leftSum = INT_MIN; 42 int m_rightSum = INT_MIN; 43 44 int m_maxLeft = mid; 45 int m_maxRight = mid + 1; 46 47 int sum = 0; 48 49 for (int i = mid; i >= low; i--) 50 { 51 sum += m_array[i]; 52 if (sum > m_leftSum) 53 { 54 m_leftSum = sum; 55 m_maxLeft = i; 56 } 57 } 58 59 sum = 0; 60 for (int i = mid + 1; i <= high; i++) 61 { 62 sum += m_array[i]; 63 if (sum > m_rightSum) 64 { 65 m_rightSum = sum; 66 m_maxRight = i; 67 } 68 } 69 70 return Tuple(m_maxLeft, m_maxRight, m_leftSum + m_rightSum); 71 } 72 73 Tuple find_maximum_subarray(int low, int high) 74 { 75 if (low == high) 76 { 77 return Tuple(low, high, m_array[low]); 78 } 79 else if (low < high) 80 { 81 int mid = (low + high) / 2.0; 82 Tuple tLeft = find_maximum_subarray(low, mid); 83 84 Tuple tRight = find_maximum_subarray(mid + 1, high); 85 86 Tuple tCross = find_max_crossing_subarray(low, mid, high); 87 88 if (tLeft.sum >= tRight.sum && tLeft.sum >= tCross.sum) 89 { 90 return tLeft; 91 } 92 else if (tRight.sum >= tLeft.sum && tRight.sum >= tCross.sum) 93 { 94 return tRight; 95 } 96 else 97 { 98 return tCross; 99 } 100 } 101 } 102 }; 103 };
main.cpp
1 #include<iostream> 2 #include "calc_max_subarray.h" 3 4 using namespace std; 5 using namespace nsp_subarray; 6 7 int main() 8 { 9 SubArray a; 10 Tuple t; 11 12 a.init_data("A.txt"); 13 14 t = a.find_maximum_subarray(0, a.get_array_size() - 1); 15 16 return 0; 17 }
6. 文件内容
文件为: A.txt,内容如下.
13 -3 -25 20 -3 -16 -23 18 20 -7 12 -5 -22 15 -4 7
链接:http://pan.baidu.com/s/1gdz35gn 密码:0id2




