LUP分解法求解线性方程组
本节我们讨论如何用LUP分解法求解线性方程组,对于含有n个未知变量x1,x2,x3,…,xn的线性方程组:
同时满足方程组中所有方程的一个数值集:x1,x2,…,xn称为方程组的解。
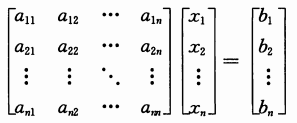
将方程组改写成矩阵向量等式:
记为:
Ax=b
如果A为非奇异矩阵,那么A存在逆矩阵,亦即方程组有解。
LUP分解的思想是找出三个n*n的矩阵,L、U和P,满足
PA=LU
其中,L是一个单位下三角矩阵,U是一个上三角矩阵,P是一个置换矩阵。则称满足上述等式的L、U和P为矩阵A的LUP分解。
等式Ax=b两边同乘以P,变形为PAx=Pb,亦即:
LUx=Pb
设y=Ux,其中x就是我们要求的向量解。我们首先通过正向替换求解下三角系统:
Ly=Pb
得到未知变量y。然后,通过正向替换求解上三角系统:
Ux=y
得到未知变量x。
由于置换矩阵P是可逆的,等式PA=LU两边同乘以P-1,得:
A=P-1LU
=P-1Ly
=P-1Pb
=b
于是x就是Ax=b的解。
调用方法:
linear::CLinearEqualtion l(3); l.init_A("A.txt"); l.init_b("b.txt"); l.lu_decomposition(); l.lup_solve(); l.show_y(); l.show_x(); l.save_solution();
C++实现:
#include <iostream> #include <vector> #include <cassert> #include <fstream> using namespace std; namespace linear { #define array_1(__type) std::vector<__type> #define array_2(__type) std::vector<array_1(__type)> class CLinearEqualtion { /* 使用方法: 1. 定义计算方程组的类对象,并初始化其系数矩阵的大小 linear::CLinearEqualtion l(3); 2. 读取系数阵 A l.init_A("A.txt"); 3. 读取 b l.init_b("b.txt"); 4. 对系数矩阵进行lu分解 l.lu_decomposition(); 5. 求解方程组 l.lup_solve(); 6. 显示反向替换的解 l.show_y(); 7. 显示正向替换的解 l.show_x(); 8. 保存方程的解 l.save_solution(); A.txt 1 5 4 2 0 3 5 8 2 b.txt 12 9 5 x[0] = -0.157895 x[1] = -0.0526316 x[2] = 3.10526 */ private: array_2(double) A; array_2(double) L; array_2(double) U; array_1(double) b; array_1(int) p; array_1(double) x; array_1(double) y; public: CLinearEqualtion(int n) { assert(n>1); A = array_2(double)(n); L = array_2(double)(n); U = array_2(double)(n); for (int i= 0; i < n;i++) { A[i] = array_1(double)(n); L[i] = array_1(double)(n); U[i] = array_1(double)(n); } b = array_1(double)(n); x = array_1(double)(n); y = array_1(double)(n); p = array_1(int)(n); } // !CLinearEqualtion(int n) virtual ~CLinearEqualtion(){} // !virtual ~CLinearEqualtion() public: void init_A(array_2(double) _A) { for (int i = 0; i < _A.size(); i++) A[i].assign(_A[i].begin(), _A[i].end()); } // !void init_A(array_2(double) _A) void init_A(std::string _fileName) { std::ifstream in(_fileName.c_str()); int i = 0; int j = 0; while(!in.eof()) { double e = 0; in>>e; std::cout<<e<<std::endl; A[i][j] = e; if (j==A.size() - 1) { i++; j = 0; } else { j++; } } } // !void init_A(std::string _fileName) void init_b(std::string _fileName) { std::ifstream in(_fileName.c_str()); int i = 0; while(!in.eof()) { double e = 0; in>>e; std::cout<<e<<std::endl; b[i++] = e; } } // !void init_b(std::string _fileName) void lu_decomposition() { int n = A.size(); // get array size for (int i = 0; i < n; i++) p[i] = i; for (int k = 0; k < n; k++) { int max = 0; int k_ = k; // get max e in col k. for (int i = k; i < n; i++) { if (fabs(A[i][k]) > max) { max = fabs(A[i][k]); k_ = i; } } // make sure not all is zero. if (max == 0) assert("singular matrix"); // swap cur row,max row. if (k != k_) { swap(p[k], p[k_]); for (int i = 0; i < n; i++) swap(A[k][i], A[k_][i]); } for (int i = k + 1; i < n; i++) { // gen v A[i][k] /= A[k][k]; for (int j = k + 1; j < n; j++) { A[i][j] -= A[i][k] * A[k][j]; } } } init_LU(); } // !void lu_decomposition() void init_LU() { int n = A.size(); // get array size for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { if (i > j) { L[i][j] = A[i][j]; } else { U[i][j] = A[i][j]; if (i == j) L[i][i] = 1; } } } } // !void init_LU() void lup_solve() { int n = A.size(); int i = 0, j = 0; for (i = 0; i < n; i++) { x[i] = 0; y[i] = 0; } for (i = 0; i < n; i++) { y[i] = b[p[i]]; for (j = 0; j < i; j++) y[i] -= L[i][j] * y[j]; } for (i = n - 1; i >= 0; i--) { double delt = y[i]; for (j = n - 1; j > i; j--) delt -= U[i][j] * x[j]; x[i] = delt / U[i][j]; } } // !void lup_solve() void show_y() { int n = A.size(); std::cout << "###" << std::endl; for (int i = 0; i < n; i++) { std::cout << "y[" << i << "]=" << y[i] << std::endl; } } // !void show_y() void show_x() { int n = A.size(); std::cout << "###" << std::endl; for (int i = 0; i < n; i++) std::cout << "x[" << i << "]=" << x[i] << std::endl; } // !void show_x() void save_solution() { int n = A.size(); ofstream out("result.txt", ios::out); out << "-------------------------------------" << std::endl; std::cout << "-------------------------------------" << std::endl; for (int i = 0; i < n; i++) { out << "x[" << i << "] = " << x[i]<< std::endl; std::cout << "x[" << i << "] = " << x[i]<< std::endl; } out << "-------------------------------------" << std::endl; std::cout << "-------------------------------------" << std::endl; out.close(); } }; }
链接:http://pan.baidu.com/s/1hqJes4k 密码:elwz


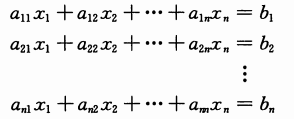



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· winform 绘制太阳,地球,月球 运作规律
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 上周热点回顾(3.3-3.9)