八大排序之交换类排序
冒泡排序#
依次比较两个相邻的两个记录的关键字,若两个记录是反序的(即前一个记录的关键字大于后一个记录的关键字),进行交换,直到没有反序的记录为止。
一趟冒泡排序#
对a[0]与a[1]的关键字比较大小,若反序,交换位置;然后比较a[1]与a[2]的关键字大小,若反序,交换位置。
以此类推,直到比较到最后两个关键字为止,称为一趟冒泡排序。
示例#
对序列:6,5,8,4,3,1 进行一趟冒泡排序
- 图中灰色部分代表需要比较的元素
参考网址:https://www.geeksforgeeks.org/bubble-sort/
Example:
First Pass:
( 5 1 4 2 8 ) –> ( 1 5 4 2 8 ), Here, algorithm compares the first two elements, and swaps since 5 > 1.
( 1 5 4 2 8 ) –> ( 1 4 5 2 8 ), Swap since 5 > 4
( 1 4 5 2 8 ) –> ( 1 4 2 5 8 ), Swap since 5 > 2
( 1 4 2 5 8 ) –> ( 1 4 2 5 8 ), Now, since these elements are already in order (8 > 5), algorithm does not swap them.
Second Pass:
( 1 4 2 5 8 ) –> ( 1 4 2 5 8 )
( 1 4 2 5 8 ) –> ( 1 2 4 5 8 ), Swap since 4 > 2
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
Now, the array is already sorted, but our algorithm does not know if it is completed. The algorithm needs one whole pass without any swap to know it is sorted.
Third Pass:
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
// C++ program for implementation of Bubble sort #include <bits/stdc++.h> using namespace std; void swap(int *xp, int *yp) { int temp = *xp; *xp = *yp; *yp = temp; } // A function to implement bubble sort void bubbleSort(int arr[], int n) { int i, j; for (i = 0; i < n-1; i++) // Last i elements are already in place for (j = 0; j < n-i-1; j++) if (arr[j] > arr[j+1]) swap(&arr[j], &arr[j+1]); } /* Function to print an array */ void printArray(int arr[], int size) { int i; for (i = 0; i < size; i++) cout << arr[i] << " "; cout << endl; } // Driver code int main() { int arr[] = {64, 34, 25, 12, 22, 11, 90}; int n = sizeof(arr)/sizeof(arr[0]); bubbleSort(arr, n); cout<<"Sorted array: \n"; printArray(arr, n); return 0; }
记法:#
- 先做一趟冒泡排序,第一个元素依次与后面的元素比较,大于(前小后大)则交换位置,最后一个元素不用比较
- 逐渐缩小一趟冒泡排序的范围,从最后一个元素开始依次缩小
时间复杂度分析#
O(n²)#
- 最好的情况,O(n)
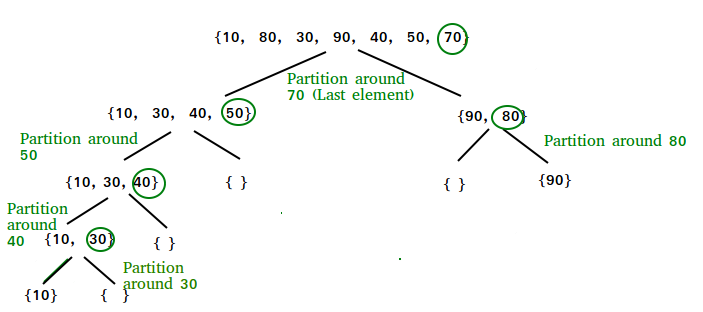
快速排序#
-
首先设定一个分界值(枢轴),通过该分界值将数组分成左右两部分
-
将大于或等于分界值的数据集中到数组右边,小于分界值的数据集中到数组的左边
-
此时,左边部分中各元素都小于或等于分界值,而右边部分中各元素都大于或等于分界值
-然后,左边和右边的数据可以独立排序 -对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值 -右侧的数组数据也可以做类似处理
-
重复上述过程,可以看出,这是一个递归定义
-
通过递归将左侧部分排好序后,再递归排好右侧部分的顺序
-
当左、右两个部分各数据排序完成后,整个数组的排序也就完成了
#
快排例述#
-
通过划分操作实现排序,以升序为例
-
每一趟选择当前所有子序列中的一个关键字作为枢轴(通常是第一个),将子序列中比枢轴小的移到枢轴前面,比枢轴大的移到枢轴后面
#
一趟快速排序#
- 对序列:6,5,8,4,3,1 进行快速排序,写出第一趟划分的过程。
| 0 | 1 | 2 | 3 | 4 | 5 | ▢ |
|---|---|---|---|---|---|---|
| 6 | 5 | 8 | 4 | 3 | 1 | 枢轴:6 |
| i | j | ▢ |
使用j,从序列最右端开始扫描,直到遇到比枢轴6小的数1,停下,将1交换到序列前端i的位置。
| 0 | 1 | 2 | 3 | 4 | 5 | ▢ |
|---|---|---|---|---|---|---|
| 1 | 5 | 8 | 4 | 3 | 枢轴:6 | |
| i | j | ▢ |
使用i,从序列最左端开始扫描,直到遇到比枢轴6大的数8,停下,将8交换到序列后端j的位置。
| 0 | 1 | 2 | 3 | 4 | 5 | ▢ |
|---|---|---|---|---|---|---|
| 1 | 5 | 4 | 3 | 8 | 枢轴:6 | |
| i | j | ▢ |
使用j,从右端往左扫描,直到遇到比枢轴6小的数3,停下,将3交换到序列前端i的位置。
| 0 | 1 | 2 | 3 | 4 | 5 | ▢ |
|---|---|---|---|---|---|---|
| 1 | 5 | 3 | 4 | 8 | 枢轴:6 | |
| i | j | ▢ |
使用i,从左端往右扫描,找不到比枢轴6大的数,直到i与j重合,停下,将枢轴6放到该位置。
| 0 | 1 | 2 | 3 | 4 | 5 | ▢ |
|---|---|---|---|---|---|---|
| 1 | 5 | 3 | 4 | 6 | 8 | 枢轴:6 |
| ij | ▢ |
第一趟划分结束
- 按同样的方法,将序列{1,5,3,4}和序列{8}进行划分,经过几趟划分,最终得到确定的有序序列。
参考网址:https://www.geeksforgeeks.org/quick-sort/
/* low --> Starting index, high --> Ending index */ quickSort(arr[], low, high) { if (low < high) { /* pi is partitioning index, arr[pi] is now at right place */ pi = partition(arr, low, high); quickSort(arr, low, pi - 1); // Before pi quickSort(arr, pi + 1, high); // After pi } }
/* C++ implementation of QuickSort */ #include <bits/stdc++.h> using namespace std; // A utility function to swap two elements void swap(int* a, int* b) { int t = *a; *a = *b; *b = t; } /* This function takes last element as pivot, places the pivot element at its correct position in sorted array, and places all smaller (smaller than pivot) to left of pivot and all greater elements to right of pivot */ int partition (int arr[], int low, int high) { int pivot = arr[high]; // pivot int i = (low - 1); // Index of smaller element for (int j = low; j <= high - 1; j++) { // If current element is smaller than the pivot if (arr[j] < pivot) { i++; // increment index of smaller element swap(&arr[i], &arr[j]); } } swap(&arr[i + 1], &arr[high]); return (i + 1); } /* The main function that implements QuickSort arr[] --> Array to be sorted, low --> Starting index, high --> Ending index */ void quickSort(int arr[], int low, int high) { if (low < high) { /* pi is partitioning index, arr[p] is now at right place */ int pi = partition(arr, low, high); // Separately sort elements before // partition and after partition quickSort(arr, low, pi - 1); quickSort(arr, pi + 1, high); } } /* Function to print an array */ void printArray(int arr[], int size) { int i; for (i = 0; i < size; i++) cout << arr[i] << " "; cout << endl; } // Driver Code int main() { int arr[] = {10, 7, 8, 9, 1, 5}; int n = sizeof(arr) / sizeof(arr[0]); quickSort(arr, 0, n - 1); cout << "Sorted array: \n"; printArray(arr, n); return 0; }
时间复杂度分析#
-
快速排序最好情况下的时间复杂度为O(nlog2n),待排序列越接近无序,该算法效率越高
-
最坏情况下的时间复杂度O(n^2),待排序序列越有序,该算法效率越低
-
平均情况下时间复杂度为O(nlog2n)
-
快速排序的排序趟数,与初始序列有关
空间复杂度分析#
- 该算法空间复杂度为O(log2n),快速排序是递归进行的,递归需要栈的辅助
作者:BigBender
出处:https://www.cnblogs.com/BigBender/p/13388819.html
版权:本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议进行许可。






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!