一元函数微分概念与计算（二）

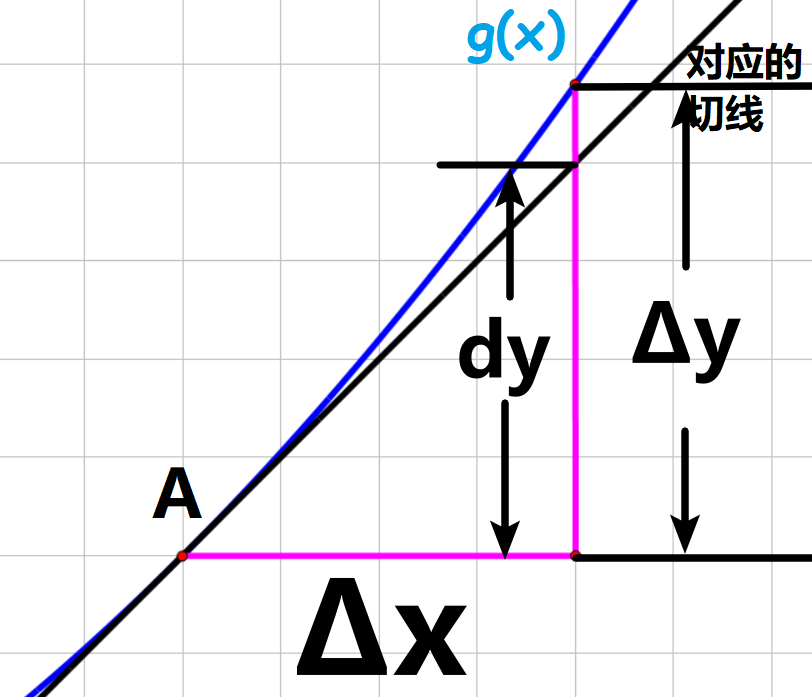
微分及其误差

 

分段函数的导数

 

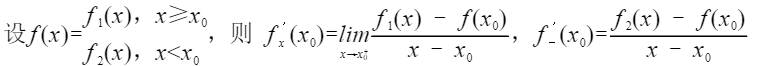
 根据左导数 是否等于 右导数，判定 f '(x₀) 

例题，y = ln|x|，求y'

一阶微分形式不变

df(u) = f ' (u)du，用链式求导法则，求到底

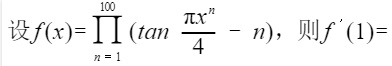
常见的导数

 

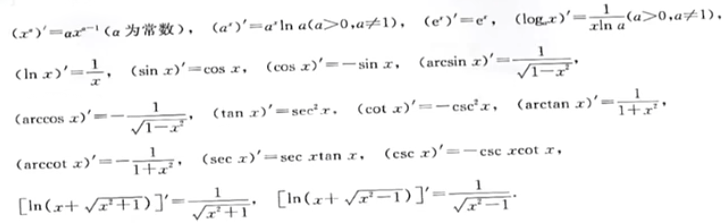
(ln |x|)' = 1/x   （ln |u(x)|)' = u'(x)/u(x)

 

反函数的导数

• 设y = f(x)可导，且f'(x)≠0，则 f'(x)必保号（恒正或者恒负），f(x)必单调 （单调递增或单调递减）
• 互为反函数的导数互为倒数

利用反函数求导数

 

 参数方程二阶导

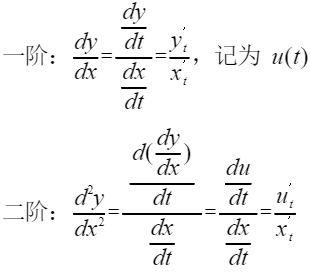
隐函数求导法

对数求导法则

• 多项相乘，相除，乘方，开方，取对数，再进行运算
• 取对数时要注意绝对值

幂指函数求导

 

高阶导数 

 

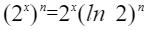
高阶求导公式

 

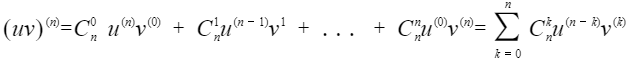
用泰勒公式（在非零点展开）

麦克劳林公式（在零点展开）

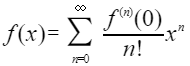
麦克劳林公式与级数展开式结合求高阶导数

诱导公式

 

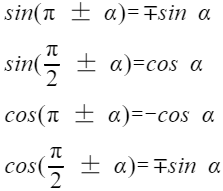
常用的级数