机器学习可解释性--LIME

A Unified Approach to Interpreting Model Predictions
trusting a prediction or trusting a model

如果⼀个机器学习模型运⾏良好，为什么我们仅仅信任该模型⽽忽略为什么做出特定的决策呢？
诸如分类准确性之类的单⼀指标⽆法完整地描述⼤多数实际任务。当涉及到预测模型时，需要作出权衡：你是只想知道预测是什么？例如，客户流失的概率或某种药物对病⼈的疗效。还是想知道为什么做出这样的预测？这种情况下可能为了可解释性付出预测性能下降的代价。在某些情况下，你不必关⼼为什么要做出这样的预测，只要知道模型在测试数据集的预测性能良好就⾜够了。但是在其他情况下，了解 “为什么” 可以帮助你更多地了解问题、数据以及模型可能失败的原因。有些模型可能不需要解释，因为它们是在低风险的环境中使⽤的，这意味着错误不会造成严重后果 (例如，电影推荐系统)，或者该⽅法已经被⼴泛研究和评估 (例如，光学字符识别 OCR)。对可解释性的需求来⾃问题形式化的不完整性，这意味着对于某些问题或任务，仅仅获得预测结果是不够的。该模型还必须解释是怎么获得这个预测的，因为正确的预测只部分地解决了你的原始问题。

机器学习可解释性

需要建立一个解释器来解释黑盒模型，并且这个解释器必须满足以下特征：
可解释性
要求解释器的模型与特征都必须是可解释的，像决策树、线性模型都是很适合拿来解释的模型；而可解释的模型必须搭配可解释的特征，才是真正的可解释性，让不了解机器学习的人也能通过解释器理解模型。
局部保真度
既然我们已经使用了可解释的模型与特征，就不可能期望简单的可解释模型在效果上等同于复杂模型（比如原始CNN分类器）。所以解释器不需要在全局上达到复杂模型的效果，但至少在局部上效果要很接近，而此处的局部代表我们想观察的那个样本的周围。
与模型无关
这里所指的是与复杂模型无关，换句话说无论多复杂的模型，像是SVM或神经网络，该解释器都可以工作。
除了传统的特征重要性排序外，ICE、PDP、SDT、LIME、SHAP都是揭开机器学习模型黑箱的有力工具。

  • 特征重要性计算依据某个特征进行决策树分裂时，分裂前后的信息增益（基尼系数）；
  • ICE和PDP考察某项特征的不同取值对模型输出值的影响；
  • SDT用单棵决策树解释其它更复杂的机器学习模型；
  • LIME的核心思想是对于每条样本，寻找一个更容易解释的代理模型解释原模型；
  • SHAP的概念源于博弈论，核心思想是计算特征对模型输出的边际贡献；

1、机器学习可解释性--LIME
2、机器学习可解释性--SHAP

机器学习可解释性--LIME

目录

机器学习的解释性

Trusting a prediction, i.e. whether a user trusts an individual prediction sufficiently to take some action based on it, and trusting a model, i.e. whether the user trusts a model to behave in reasonable ways if deployed.” (Ribeiro 等, 2016, p. 1135)

信任一个预测，即用户是否充分信任一个个体的预测，并在此基础上采取行动；信任一个模型，即用户是否信任一个模型在部署后的行为是否合

LIME, an algorithm that can explain the predictions of any classifier or regressor in a faithful way, by approximating it locally with an interpretable model.” (Ribeiro 等, 2016, p. 1135)

LIME是一种算法，通过用可解释的模型对其进行局部近似，可以忠实地解释任何分类器或回归器的预测。

所谓机器学习可解释性就是：我们建立了一个模型预测得到了一个结果，但是你这个结果真的可以让人信服吗（从实际生产角度考虑，不从模型的准确率的角度考虑）？这个模型的影响因素又是什么呢？如下图[1]：
机器学习可解释性--LIME[^2]

我们通过模型预测流感（flu），通过LIME得到的解释是：喷嚏（sneeze）、头疼（headche）对流感预测是“支持”，而没有疲劳（no fatigue）是“反对”。我们将模型结果交给决策者（human make decision）让她对模型结果做判断。机器学习只能作为我们辅助决策的工具，对于实际决策还是依靠人类。而我们的决策的依据就是解释（explainer），我们根据给出的解释来判别模型是否可作为我们的决策依据。

LIME原理

LIME（Local Interpretable Model-agnostic Explanations）。该模型是一个局部可解释模型，并且是一个与模型自身的无关的可解释方法。使用训练的局部代理模型来对单个样本进行解释。假设对于需要解释的黑盒模型，取关注的实例样本，在其附近进行扰动生成新的样本点，并得到黑盒模型的预测值，使用新的数据集训练可解释的模型（如线性回归、决策树），得到对黑盒模型良好的局部近似[2]。

“The overall goal of LIME is to identify an interpretable model over the interpretable representation that is locally faithful to the classifier.” (Ribeiro 等, 2016, p. 1137)

LIME的总体目标是基于局部可解释性模型 在局部忠实于分类器的可解释表示上识别一个可解释模型。

LIME特点如下：

  • Local：局部保证度，即我们希望解释真实反映的分类器

LIME计算

假设\(f\)作为我们需要解释的模型，那么我们定义解释模型\(g \in G\) ，\(G\)作为解释族函数（一系列可能的解释模型（线性模型、决策树模型等）），因为并不是每一个\(g\in G\)都可能是简单到可以解释的，因此定义\(\Omega(g)\)作为复杂形测度，\(\pi_{x}\)作为实例\(z\)到\(x\)之间的邻近度量，从而定义\(x\)周围的局部性。最后定义\(L(f,g,\pi_{x})\)作为不忠实\(g\)在\(\pi_{x}\)定义的局部中逼近\(f\)，为了保证可解释性和局部忠实性计算公式：

\[\xi(s)= argmin_{g\in G} L(f,g,\pi_{x})+\Omega(g) \]

局部探索

前面提及到了LIME是一种局部探索可解释模型，那么其局部探索功能如何实现呢？在论文中的3.3 Sampling for Local Exploration作者给出解释如下：
如公式1所示我们需要最小化\(L(f,g,\pi_{x})\)，我们在\(x\)周围生成扰动样本（perturbed sample）设生成的扰动样本为\(Z\)，那么我们可以根据我们的\(f\)对我们所生成的扰动样本进行处理即：\(f(Z)\)，我们对扰动样本进行加权（距离\(x\)近的赋予较大权重，反之则较小权重）

“where we sample instances both in the vicinity of \(x\) (which have a high weight due to \(\pi_{x}\)) and far away from x (low weight from \(\pi_{x}\)).” ([Ribeiro 等, 2016, p. 1137]
其中，我们分别在\(x\) (由于\(\pi_{x}\)而具有很高的权重)附近和远离\(x\) (来自\(\pi_{x}\)的低权重)的地方采样实例。

作者在论文中提到即使原始模型（\(f\)）很难全局进行解释，但是LIME能够在局部进行合理解释

ven though the original model may be too complex to explain globally, LIME presents an explanation that is locally faithful

稀疏线性解释

论文作者设置解释族函数\(G\)为线性模型（\(g(Z)=w_{g}z\)），设置\(L\)为$ \underset{z,z^{'}\in Z}{\sum}\pi_{x}(z)(f(z)-g(z{'})\(，\)\pi_{x}\(为\)exp(\frac{-D(x,z){2}}{\sigma{2}})\(，上面提及到的扰动样本\)Z\(，对于扰动样本设计线性函数去对扰动样本进行区分（已分类算法为例）那么我们所赋予的不同的权重\)w_{g}$就是不同的样本中不同特征的影响。

LIME步骤

  • 对整个数据进行训练，模型可以是Lightgbm，XGBoost等复杂的模型（本身不可解释）;
  • 选择我们想要解释的变量\(x\);
  • 对数据集中的数据进行可解释的N次扰动，生成扰动样本;
  • 对这些新的样本求出权重，这个权重是这些数据点与我们要解释的数据之间的距离;
  • 根据上面新的数据集，拟合一个简单的模型\(g\)，比如Lasso Regression得到模型的权重;
  • 通过简单模型\(g\)来对原复杂模型在\(x\)点附近进行解释;

LIME直观解释

1、分类算法

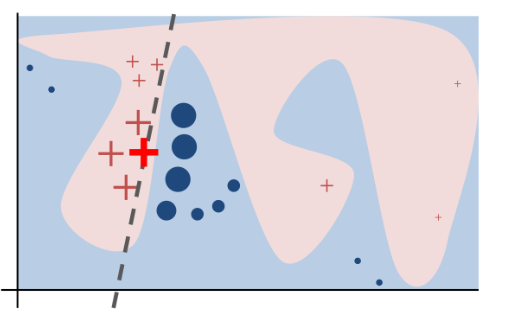
202306052009422

如上图不同的颜色块代表不同的类别（蓝色和粉色），很难通过线性模型进行近似。因此输入样本（加重红色×）在其周围生成不同的扰动样本（×和·，其大小代表距离），我们可以对所生成的扰动样本构建线性函数进行区分。具体步骤如下图所示：

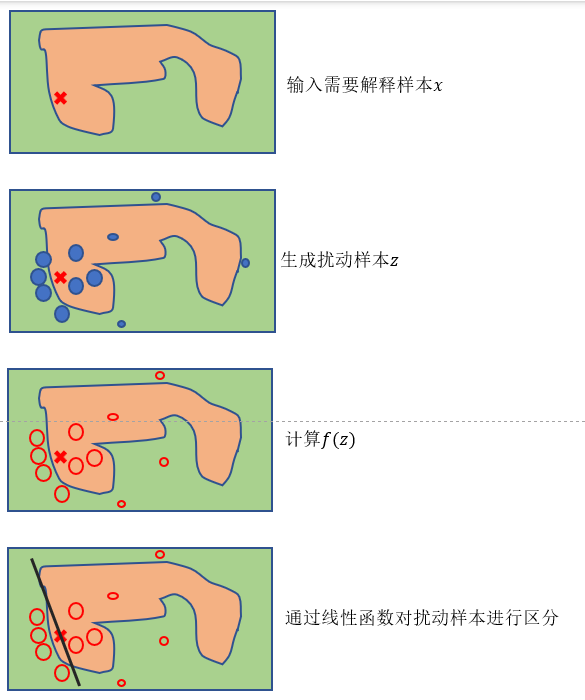
202306052008339

2、图像识别

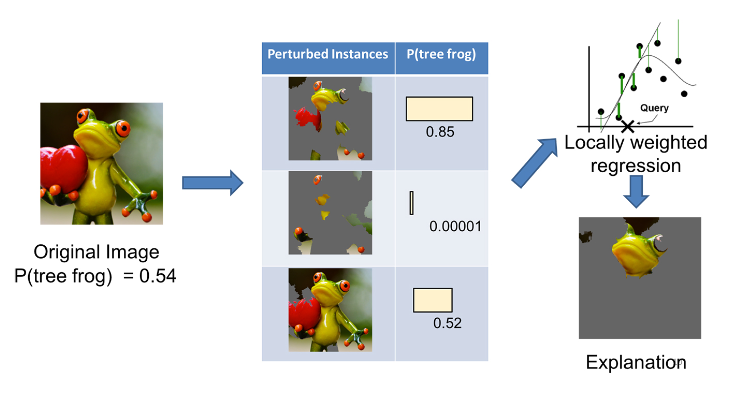
在Local Interpretable Model-Agnostic Explanations (LIME): An Introduction[3]中作者对图像识别做出了解释。对一只树蛙进行分类：

202306052008339

将一些可解释的成分 "关闭"（在这种情况下，使它们变成灰色）来生成一组扰乱实例的数据。对于每个被扰乱的实例，我们根据模型得到树蛙在图像中的概率。然后我们在这个数据集上学习一个简单的（线性）模型，这个模型是局部加权的--也就是说，我们更关心在与原始图像更相似的扰动实例中犯错误。最后，我们将具有最高正向权重的超级像素作为解释，而将其他的东西涂成灰色。

202306052008339

我们在任意图像上解释谷歌的 Inception 神经网络。在这种情况下，如下图 所示，分类器将“树蛙”预测为最有可能的类别，其次是概率较低的“台球桌”和“气球”。解释表明分类器主要关注青蛙的脸作为对预测类别的解释。它还阐明了为什么“台球桌”的概率不为零：青蛙的手和眼睛与台球很相似，尤其是在绿色背景下。同样，爱心也很像一个红色的气球。

202306052008339

LIME优缺点

1、LIME算法有很强的通用性，效果好。LIME除了能够对图像的分类结果进行解释外，还可以应用到自然语言处理的相关任务中，如主题分类、词性标注等。因为LIME本身的出发点就是模型无关的，具有广泛的适用性。

2、LIME算法速度慢，LIME在采样完成后，每张采样出来的图片都要通过原模型预测一次结果，所以在速度上没有明显优势。

3、LIME算法拓展方向，本文的作者在18年新提出了Anchors的方法，指的是复杂模型在局部所呈现出来的很强的规则性的规律，注意和LIME的区别，LIME是在局部建立一个可理解的线性可分模型，而Anchors的目的是建立一套更精细的规则系统。在和文本相关的任务上有不错的表现。有待我们继续研究。

优点：

  • 表格型数据、文本和图片均适用；
  • 解释对人友好，容易明白；
  • 给出一个忠诚性度量，判断可解释模型是否可靠；
  • LIME可以使用原模型所用不到的一些特征数据，比如文本中一个词是否出现。

缺点：

  • 表格型数据中，相邻点很难定义，需要尝试不同的kernel来看LIME给出的可解释是否合理；
  • 扰动时，样本服从高斯分布，忽视了特征之间的相关性；
  • 稳定性不够好，重复同样的操作，扰动生成的样本不同，给出的解释可能会差别很大。

参考

  1. https://doi.org/10.1145/2939672.2939778 ↩︎

  2. https://blog.csdn.net/iqdutao/article/details/108397239 ↩︎

  3. https://www.oreilly.com/content/introduction-to-local-interpretable-model-agnostic-explanations-lime/ ↩︎

posted @ 2024-02-24 21:32  Big-Yellow-J  阅读(61)  评论(0)  编辑  收藏  举报