R1(下)—数据挖掘—关联规则理论介绍与R实现
Apriori algorithm是关联规则里一项基本算法。是由Rakesh Agrawal和Ramakrishnan Srikant两位博士在1994年提出的关联规则挖掘算法。关联规则的目的就是在一个数据集中找出项与项之间的关系,也被称为购物蓝分析 (Market Basket analysis),因为"购物蓝分析"很贴切的表达了适用该算法情景中的一个子集。
关于这个算法有一个非常有名的故事:"尿布和啤酒"。故事是这样的:美国的妇女们经常会嘱咐她们的丈夫下班后为孩子买尿布,而丈夫在买完尿布后又要顺 手买回自己爱喝的啤酒,因此啤酒和尿布在一起被购买的机会很多。这个举措使尿布和啤酒的销量双双增加,并一直为众商家所津津乐道。
-
图解



-
关联规则概念介绍
资料库(Transaction Database):存储着二维结构的记录集。定义为:D
所有项集(Items):所有项目的集合。定义为:I。
记录 (Transaction ):在资料库里的一笔记录。定义为:T,T ∈ D
项集(Itemset):同时出现的项的集合。定义为:k-itemset(k项集),k-itemset ? T。除非特别说明,否则下文出现的k均表示项数。
支持度(Support):定 义为 supp(X) = occur(X) / count(D) = P(X)。
1. 解释一:比如选秀比赛,那个支持和这个有点类似,那么多人(资料库),其中有多少人是选择(支持)你的,那个就是支持度;
2. 解释二:在100个人去超市买东西的,其中买苹果的有9个人,那就是说苹果在这里的支持度是 9,9/100;
3. 解释三:P(X),意思是事件X出现的概率;
4. 解释四:关联规则当中是有绝对支持度(个数)和相对支持度(百分比)之分的。
置信度(Confidence/Strength): 定义为 conf(X->Y) = supp(X ∪ Y) / supp(X) = P(Y|X)。
候选 集(Candidate itemset):通过向下合并得出的项集。定义为C[k]。
频繁集(Frequent itemset):支持度大于等于特定的最小支持度(Minimum Support/minsup)的项集。表示为L[k]。注意,频繁集的子集一定是频繁集。
提升比率(提升度Lift):lift(X -> Y) = lift(Y -> X) = conf(X -> Y)/supp(Y) = conf(Y -> X)/supp(X) = P(X and Y)/(P(X)P(Y))
经过关联规则分析后,针对某些人推销(根据某规则)比盲目推销(一般来说是整个数据)的比率,这个比率越高越好,我们称这个规则为强规则;
剪枝步
只有当子集都是频繁集的候选集才是频繁集,这个筛选的过程就是剪枝步;
• More information about the concepts of arules!
1、项集(Itemset):是一组项,而每一个项都是一个属性值。在购物篮分析示例中,项集包含一组产品,例如Cake、Pepsi、Milk。在研究客户的人口统计信息示例中,项集包含一组属性值,比如{Gender='Male',Education='Bachelor'}。每个项集都有一个大小,该大小表示项集中包含的项的数目。项集{Cake、Pepsi、Milk}的大小是3。
频繁项集是在数据集中出现频率相当高的那些项集。项集出现频率的阈值是用"支持度"来定义的。
2、支持度(Support):支持度用来度量一个项集的出现频率。项集{A,B}的支持度是同时包含A和B的事务的总个数。即:
Support({A,B})=NumberofTransactions(A,B)
Minimum_Support是一个阈值参数,必须在处理关联模型之前指定该参数。该参数表示用户只对某些项集和规则感兴趣,这些规则表示数据集的最低支持度。它是用于对项集进行限制,而不是对规则进行限制。
3、概率(Probability):也叫置信度(Confidence),是关联规则的属性。规则A=>B要概率是使用{A}的支持度除项集{A,B}的支持度来计算的。公式如下:
Probability(A=>B)=Probability(B|A)=Support(A,B)/Support(A)
也等于NumberofTransactions(A,B)/TotalNumberofTransactions
Minimum_Probability是一个阈值参数,必须在运行算法之前指定该参数.它表用户只对某些规则感兴趣,这些规则摇拥有比较高的概率,而不是最小的概率.Minimum_Probability对项集没有任何影响,它影响的是规则.
3、重要性(Importance):在一些文献中也称为兴趣度分数或者增益。重要性可以用于度量项集和规则。
项集的重要性是使用以下公式来定义的:
如果Importance=1,刚A和B是独立的项,它表示购买A和购买B是两个独立的事件。如果Importance<1,刚A和B是负相关的,这表求如果一个客户购买A了,刚他购买B是不太可能发生的。如果Importance>1,刚A和B是正相关的。这表示如果一个客户购买了A,刚他也可能购买B。
规则的重要性是使用以下公式计算的:
Importance(A=>B)=Log(P(B|A)/P(B|not A))
重要性为0,表示A和B之间没有任何关联。正的重要性分数表示当A为真时,B的概率会上升。负的重要性分数表示,当A为真时,B的概率会下降。
-
简单例子

-
R实现

纲要(Outline)
介绍(Introduction)
关联规则挖掘(Association Rule Mining)
去除冗余(Removing Redundancy)
关联规则解读(Interpreting Rules)
关联规则可视化(Visualizing Association Rules)
补充阅读和在线资源(Further Reading and Online Resources)

介绍
一句话关联规则:关联规则是展现项集(itemsets)间关联(association)与相关性(correlation)的规则!
几个重要公式:
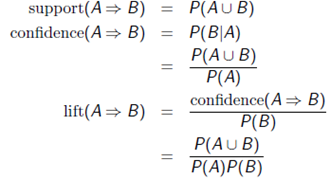
P(A)是包含A项的case(这里的cases即为数据库中的transaction每笔交易记录)百分比或概率!
R中的关联规则挖掘算法:APRIORI和ECLAT算法
APRIORI是一种计算交易记录(transaction)来发现频繁项集,然后从这些频繁项集中导出(derive)关联规则的逐层(level-wise)、宽度优先(breadth-first)算法、也是最有影响的挖掘布尔关联规则频繁项集的算法。其核心是基于两阶段频集思想的递推算法!
Apriori()算法在arules包中已实现!
ECLAT算法的特点是发现具有等价类的频繁项集(equivalence class),深度优先搜索,集合相交(set intersection)而不是计数(counting)
Eclat()算法也在arules包中!
关联规则挖掘
泰坦尼克号数据集(The Titanic Dataset):
在数据集包中的泰坦尼克号数据集是一个四维表,它根据社会地位(social class)、性别、年龄、和是否幸存(survival)汇总了在泰坦尼克号上的乘客命运的信息!
为了使得该数据集适用于关联规则挖掘,我们对原始数据进行了一下简答的重构,命名为Titanic.raw,其中每一行代表一个人!重构后的数据集可以在http://www.rdatamining.com/data/titanic.raw.rdata 进行下载!
Step1:加载数据集查看统计描述信息
> library(arules)
> path.package(package = 'arules')
[1] "C:/Users/wb-tangyang.b/Documents/R/win-library/3.1/arules" #查看arules包所在路径
> load(file = 'E:/文档/2015/校外/tangyang/学习/R笔记/1-数据分析与挖掘/数据挖掘算法-R运用/01-关联规则(市场篮子分析!)/datasets/titanic.raw.rdata') #这个数据集是通过上面上面那个链接先下载下来,然后在这儿进行加载,导入到R中!
> idx<-sample(1:nrow(titanic.raw),5)
> titanic.raw[idx,]
Class Sex Age Survived
1699 Crew Male Adult Yes
1977 1st Female Adult Yes
2200 Crew Female Adult Yes
1457 3rd Female Adult No
2170 3rd Female Adult Yes
> summary(titanic.raw)
Class Sex Age Survived
1st :325 Female: 470 Adult:2092 No :1490
2nd :285 Male :1731 Child: 109 Yes: 711
3rd :706
Crew:885
Step2:apriori()函数
使用Aprior算法挖掘频繁项集,关联规则或者关联超边(hyperedge),Aprior算法运用逐层(level-wise)方法搜索频繁项集。
其关于支持度、置信度、最大规则长度的默认设置如下:
-
minimum support: supp=0.1
-
minimum condence: conf=0.8
-
maximum length of rules: maxlen=10

#####用法说明
apriori(data, parameter = NULL, appearance = NULL, control = NULL)
#####参数说明
Data:交易数据(transactions)类对象或任何能够被转化成transaction的数据结构
Parameter:APparameter类对象或命名列表。挖掘规则默认的行为是:支持度=0.1;置信度=0.8;输出的最大规则长度;
Appearance:APappearance类对象或命名列表。
Control:APcontrol类对象或命名列表。控制挖掘算法的性能!
####细节说明
APparameter中minlen(最小规则数)默认的值是1,这意味着将会产生只有一项(item:比如,先前项/LHS)的规则:{}=>{beer}—这项规则说明,no matter what other items are involved the item in the RHS will appear with the probability given by the rule's confidence (which equals the support)。如果想要避免这些规则,可以使用参数:parameter=list(minlen=2)!
####返回值说明:返回一个rules类对象或itemsets类对象。

step3:运用apriori函数进行关联规则分析
1)关联规则—默认参数
> rules.all<-apriori(titanic.raw)
 > inspect(rules.all)
> inspect(rules.all)

<注> lhs=left hand side;rhs=right hand side.
2)关联规则—调整参数
#如果只想检查其它变量和乘客是否幸存的关系,那么需要提前设置变量rhs=c("Survived=No", "Survived=Yes")
######rules with rhs containing "Survived" only!
rules <- apriori(titanic.raw,
control = list(verbose=F),
parameter = list(minlen=2, supp=0.005, conf=0.8),
appearance = list(rhs=c("Survived=No","Survived=Yes"),
#现在生成的关联规则结果只包含("Survived=No", "Survived=Yes")
default="lhs"))
@结果
> rules
set of 12 rules
> quality(rules)
support confidence lift
1 0.010904134 1.0000000 3.095640
2 0.042253521 0.8773585 2.715986
3 0.069968196 0.8603352 1.270871
4 0.064061790 0.9724138 3.010243
5 0.009086779 0.8695652 2.691861
6 0.191731031 0.8274510 1.222295
7 0.005906406 1.0000000 3.095640
8 0.036347115 0.8602151 2.662916
9 0.069968196 0.9166667 1.354083
10 0.063607451 0.9722222 3.009650
11 0.009086779 0.8695652 2.691861
12 0.175829169 0.8376623 1.237379
######keep three decimal places
> quality(rules) <- round(quality(rules), digits=3)
> quality(rules)
support confidence lift
1 0.011 1.000 3.096
2 0.042 0.877 2.716
3 0.070 0.860 1.271
4 0.064 0.972 3.010
5 0.009 0.870 2.692
6 0.192 0.827 1.222
7 0.006 1.000 3.096
8 0.036 0.860 2.663
9 0.070 0.917 1.354
10 0.064 0.972 3.010
11 0.009 0.870 2.692
12 0.176 0.838 1.237
####order rules by lift(根据关联结果中的提升度(life)进行降序排序)
> rules.sorted <- sort(rules, by="lift")
####检查排序后的变量
> inspect(rules.sorted)

去除冗余(Removing Redundancy)
> inspect(rules.sorted[1:2])

规则#2未能在规则#1之上提供更多的信息,因为规则#1已经告诉我们:所有的2nd-class children都幸存啦!也就是说实际上规则2只是规则1的超集!!!
请记住去除冗余的一项规则:当一个规则(比如:规则#2)是另一个规则(比如#1)的父规则。前者有相同或更低的lift(提升度),前面的规则(规则#2)就被认为是冗余(redundant)的,即留下子规则child rules!
由此可见,上述其他冗余规则还有是#4、#7和#8,与只对应的是规则#3、#6、#5!
#####发现冗余规则!

插播—函数介绍:
- Is.subset(x,y=NULL, proper=FALSE, sparse=FALSE,...) #is.subset和is.superset函数用于在关联和项集矩阵对象中发现子集或父集!
- Lower.tri(x,diag=FALSE) #返回一个与给定矩阵(在上三角或下三角中TRUE)相同大小的逻辑矩阵

#####哪一个规则是冗余的?
#####生成一个关联规则的子集矩阵
> subset.matrix <- is.subset(rules.sorted, rules.sorted)
> subset.matrix #####注释:从结果中可以看到矩阵中对角线上的位置的TRUE表示12个规则,而其它行位置上TRUE则表示行坐标值代表的规则是纵坐标值代表的规则的子集。例如[2,1],[2,5]上面的TRUE,就表示规则2是规则1和规则5的子集。这个从上面的排序后的规则列表中就可以看出啦!
#####注释:从结果中可以看到矩阵中对角线上的位置的TRUE表示12个规则,而其它行位置上TRUE则表示行坐标值代表的规则是纵坐标值代表的规则的子集。例如[2,1],[2,5]上面的TRUE,就表示规则2是规则1和规则5的子集。这个从上面的排序后的规则列表中就可以看出啦!
####将矩阵对角线以下的元素置为空,这样只包含TRUE的元素列就是子规则,需要去除
> lower.tri(subset.matrix, diag = T)

> subset.matrix[lower.tri(subset.matrix, diag = T)] <- NA
> subset.matrix

####将子集矩阵中每列元素和大于等于1的列找出来
> redundant <- colSums(subset.matrix, na.rm = T) >= 1
> redundant
[1] FALSE TRUE FALSE TRUE FALSE FALSE TRUE TRUE FALSE FALSE FALSE FALSE
#####移除冗余规则!
> which(redundant)
[1] 2 4 7 8
#####从规则矩阵中去掉这些列
> rules.pruned <- rules.sorted[! redundant]
## remove redundant rules
> rules.pruned
set of 8 rules
###Remaining Rules
#####检查最终生成的结果集
> inspect(rules.pruned)

关联规则解读(Interpreting Rules)、
> inspect(rules.pruned[1])

这条规则告诉了我们什么呢?难道2nd class(二等舱)的孩子比其他孩子的幸存率更高??!
需要注意的是:这条规则仅仅讲述了所有二等舱的孩子都幸存了下来,并没有其他舱位幸存率的比较信息!
#######进一步优化(Rules about Children):
rules <- apriori(titanic.raw, control = list(verbose=F),
parameter = list(minlen=3, supp=0.002, conf=0.2),
appearance = list(default="none", rhs=c("Survived=Yes"),
lhs=c("Class=1st", "Class=2nd", "Class=3rd",
"Age=Child", "Age=Adult")))
> rules
set of 6 rules
> rules.sorted <- sort(rules, by="confidence")
> inspect(rules.sorted)

关联规则可视化(Visualizing Association Rules):使用arulesViz包!
#####加载包arulesViz, 画出关联规则的图形表示方法
> plot(rules)
> plot(rules.pruned)

> plot(rules.pruned, method = "grouped")

> plot(rules.pruned, method = "graph")

> plot(rules.pruned, method = "graph", control = list(type = "items"))

> plot(rules.pruned, method = "paracoord", control = list(reorder = TRUE))

补充阅读和在线资源(Further Reading and Online Resources)
####further readings
I More than 20 interestingness measures, such as chi-square,
conviction, gini and leverage
Tan, P.-N., Kumar, V., and Srivastava, J. (2002). Selecting the right
interestingness measure for asso ciation patterns. In Pro c. of KDD '02,
pages 32-41, New York, NY, USA. ACM Press.
I Post mining of association rules, such as selecting interesting
association rules, visualization of association rules and using
association rules for classification
Yanchang Zhao, Chengqi Zhang and Longbing Cao (Eds.). "Post-Mining
of Asso ciation Rules: Techniques for Effective Knowledge Extraction",
ISBN 978-1-60566-404-0, May 2009. Information Science Reference.
I Package arulesSequences: mining sequential patterns
http://cran.r- project.org/web/packages/arulesSequences
####online resources
I Chapter 9: Association Rules, in book
R and Data Mining: Examples and Case Studies
http://www.rdatamining.com/docs/RDataMining.pdf
I R Reference Card for Data Mining
http://www.rdatamining.com/docs/R- refcard- data- mining.pdf
I Free online courses and documents
http://www.rdatamining.com/resources/
I RDataMining Group on LinkedIn (8,000+ members)
http://group.rdatamining.com
I RDataMining on Twitter (1,800+ followers)
@RDataMining


附录 1
数据挖掘是指以某种方式分析数据源,从中发现一些潜在的有用的信息,所以数据挖掘又称作知识发现,而关联规则挖掘则是数据挖掘中的一个很重要的课题,顾名思义,它是从数据背后发现事物之间可能存在的关联或者联系。举个最简单的例子,比如通过调查商场里顾客买的东西发现,30%的顾客会同时购买床单和枕套,而购买床单的人中有80%购买了枕套,这里面就隐藏了一条关联:床单—>枕套,也就是说很大一部分顾客会同时购买床单和枕套,那么对于商场来说,可以把床单和枕套放在同一个购物区,那样就方便顾客进行购物了。下面来讨论一下关联规则中的一些重要概念以及如何从数据中挖掘出关联规则。
关联规则挖掘中的几个概念
先看一个简单的例子,假如有下面数据集,每一组数据ti表示不同的顾客一次在商场购买的商品的集合:
t1: 牛肉、鸡肉、牛奶
t2: 牛肉、奶酪
t3: 奶酪、靴子
t4: 牛肉、鸡肉、奶酪
t5: 牛肉、鸡肉、衣服、奶酪、牛奶
t6: 鸡肉、衣服、牛奶
t7: 鸡肉、牛奶、衣服
假如有一条规则:牛肉—>鸡肉,那么同时购买牛肉和鸡肉的顾客比例是3/7,而购买牛肉的顾客当中也购买了鸡肉的顾客比例是3/4。这两个比例参数是很重要的衡量指标,它们在关联规则中称作支持度(support)和置信度(confidence)。对于规则:牛肉—>鸡肉,它的支持度为3/7,表示在所有顾客当中有3/7同时购买牛肉和鸡肉,其反应了同时购买牛肉和鸡肉的顾客在所有顾客当中的覆盖范围;它的置信度为3/4,表示在买了牛肉的顾客当中有3/4的人买了鸡肉,其反应了可预测的程度,即顾客买了牛肉的话有多大可能性买鸡肉。其实可以从统计学和集合的角度去看这个问题, 假如看作是概率问题,则可以把"顾客买了牛肉之后又多大可能性买鸡肉"看作是条件概率事件,而从集合的角度去看,可以看下面这幅图:

上面这副图可以很好地描述这个问题,S表示所有的顾客,而A表示买了牛肉的顾客,B表示买了鸡肉的顾客,C表示既买了牛肉又买了鸡肉的顾客。那么C.count/S.count=3/7,C.count/A.count=3/4。
在数据挖掘中,例如上述例子中的所有商品集合I={牛肉,鸡肉,牛奶,奶酪,靴子,衣服}称作项目集合,每位顾客一次购买的商品集合ti称为一个事务,所有的事务T={t1,t2,....t7}称作事务集合,并且满足ti是I的真子集。一条关联规则是形如下面的蕴含式:
X—>Y,X,Y满足:X,Y是I的真子集,并且X和Y的交集为空集
其中X称为前件,Y称为后件。
对于规则X—>Y,根据上面的例子可以知道它的支持度(support)=(X,Y).count/T.count,置信度(confidence)=(X,Y).count/X.count 。其中(X,Y).count表示T中同时包含X和Y的事务的个数,X.count表示T中包含X的事务的个数。
关联规则挖掘则是从事务集合中挖掘出满足支持度和置信度最低阈值要求的所有关联规则,这样的关联规则也称强关联规则。
对于支持度和置信度,我们需要正确地去看待这两个衡量指标。一条规则的支持度表示这条规则的可能性大小,如果一个规则的支持度很小,则表明它在事务集合中覆盖范围很小,很有可能是偶然发生的;如果置信度很低,则表明很难根据X推出Y。根据条件概率公式P(Y|X)=P(X,Y)/P(X),即P(X,Y)=P(Y|X)*P(X)
P(Y|X)代表着置信度,P(X,Y)代表着支持度,所以对于任何一条关联规则置信度总是大于等于支持度的。并且当支持度很高时,此时的置信度肯定很高,它所表达的意义就不是那么有用了。这里要注意的是支持度和置信度只是两个参考值而已,并不是绝对的,也就是说假如一条关联规则的支持度和置信度很高时,不代表这个规则之间就一定存在某种关联。举个最简单的例子,假如X和Y是最近的两个比较热门的商品,大家去商场都要买,比如某款手机和某款衣服,都是最新款的,深受大家的喜爱,那么这条关联规则的支持度和置信度都很高,但是它们之间没有必然的联系。然而当置信度很高时,支持度仍然具有参考价值,因为当P(Y|X)很高时,可能P(X)很低,此时P(X,Y)也许会很低。
END
关联规则挖掘的原理和过程
从上面的分析可知,关联规则挖掘是从事务集合中挖掘出这样的关联规则:它的支持度和置信度大于最低阈值(minsup,minconf),这个阈值是由用户指定的。根据支持度=(X,Y).count/T.count,置信度=(X,Y).count/X.count ,要想找出满足条件的关联规则,首先必须找出这样的集合F=X U Y ,它满足F.count/T.count ≥ minsup,其中F.count是T中包含F的事务的个数,然后再从F中找出这样的蕴含式X—>Y,它满足(X,Y).count/X.count ≥ minconf,并且X=F-Y。我们称像F这样的集合称为频繁项目集,假如F中的元素个数为k,我们称这样的频繁项目集为k-频繁项目集,它是项目集合I的子集。所以关联规则挖掘可以大致分为两步:
1)从事务集合中找出频繁项目集;
2)从频繁项目集合中生成满足最低置信度的关联规则。
最出名的关联规则挖掘算法是Apriori算法,它主要利用了向下封闭属性:如果一个项集是频繁项目集,那么它的非空子集必定是频繁项目集。它先生成1-频繁项目集,再利用1-频繁项目集生成2-频繁项目集。。。然后根据2-频繁项目集生成3-频繁项目集。。。依次类推,直至生成所有的频繁项目集,然后从频繁项目集中找出符合条件的关联规则。

附录 2:Introduction to arules
- 数据结构概述
在arules(http://CRAN.R-Project.org)包中,对于输入数据集:可以是transactions类和tidLists类(交易事物表ID列表,是表示交易事物数据的另一种方式!) ;对于挖掘算法的输出:有itemsets类和rules类,分别代表项集合规则的集合。arules包中实施的S4类结构如下:

itemsets类和rules类是对提供了一个通用接口的通用虚拟类associations的扩展。在这个结构中,很容易通过添加一个扩展associations接口的新类来添加一种新的关联类型!
associations和transactions中的项(iterms)是通过itemMatrix类来实现的。ASparameter和 AScontrol两个类是用来控制挖掘算法行为的。因为每一个算法都可以使用其他特定算法的参数,我们为每一个接口算法实现了各自的控制类集。这里使用前缀"AP"来表示Apriori算法,"EC"表示Eclat算法!
#####表示项集集合(represent collection of itemsets)
事物数据库中的一条交易记录包括了一个交易ID,一个项集.挖掘到的关联规则集中,一条规则包括两个项集,一个是LHS(left hand side),一个是RHS(right hand side),以及其他优质信息(quality information),比如各种相关度量(interest measures)的值!
交易数据库使用的项集集合和关联集可以被表示成二元关联矩阵(binary incidence matrices),列对应项(items),行对应项集(itemsets)。矩阵元素/条目(entries)表示在一个特定的项集中某一项的有无(presence (1) or absence(0))
例如:将图1中的交易数据库表示成图3中的包含项集的二元关联矩阵,如下!


对于这类数据的自然表示是用一个稀疏矩阵格式。对于代码实现,我们选择了定义在Matrix包中的ngCMatrix类。
将上述稀疏矩阵的数据变成如下List格式的数据,

- 更多的例子(一大波例子来袭)
#####例子1:分析和准备一个交易数据集
该例主要说明在进行关联挖掘之前,如何分析和处理(manipulate)一个数据集。这对于发现可能会影响后续关联规则质量的问题非常重要!例如,这里使用arules包中的Epub交易数据,该数据集包括了从Vienna University of Economics and Business的Elaectronic Publication平台上的2003年1月到2008年12月的文件下载量!(http://epub.wu-wien.ac.at )
先加载arules包和Epub数据集
> library("arules")
> data(Epub)
> Epub
transactions in sparse format with
15729 transactions (rows) and
936 items (columns)
可以看到,Epub数据集包括了15729条交易记录,并用一个15729行和代表项的936列的稀疏矩阵表示!下一步,使用summary()函数来获取更多信息.
> summary(Epub)

Summary显示了数据集中最频繁项(most frequent items),交易记录长度分布的信息以及包含了一些扩展交易信息的数据集!下一步,我们使用POSIXct类来查看包含了交易IDs和时间戳的数据集,这些额外的信息可以用于分析数据集。
> year <- strftime(as.POSIXlt(transactionInfo(Epub)[["TimeStamp"]]), "%Y") #strftime进行日期和字符转化!
> table(year)
year
2003 2004 2005 2006 2007 2008 2009
986 1376 1610 3010 4052 4692 3
对于2003年,数据集中的第一年,总共有987比交易(即下载记录).下一步,选择相应的交易记录,使用level-plot来查看(inspect)其结构!
注:Epub数据集的格式如下
>transactionInfo(Epub)

> Epub2003 <- Epub[year == "2003"]
> length(Epub2003)
[1] 986
> image(Epub2003)

这幅图是二元关联矩阵的一个直接可视化,其中黑色的点(dark dots)代表对应矩阵中的值。从这幅图中,可知:数据集中的项分布不均匀(not evenly distributed).事实上,图中右边最空白的区域暗示,在2003年初,仅仅有少量的项可用(少于50)。在这一年间,更多的项被添加进来,最终到了300项左右的数量。同样,还可知:数据集中的有一些交易记录中,包含了非常高的项数(number of items)【密度较大的水平线】,这些交易记录需要进一步检查,因为他们可能是由于数据收集时产生的问题而引起(例如,一个网络机器人,从pub网站上下载了很多文档!!!)。下一步,使用size函数来选择非常长的交易记录,并从中选择非常长的交易记录(包括了超过20项!)
> transactionInfo(Epub2003[size(Epub2003) > 20])
transactionID TimeStamp
11092 session_56e2 2003-04-30 01:30:38
11371 session_6308 2003-08-18 06:16:12
我们发现了两个长交易记录(即这条交易记录包括了很多项),并打印出了响应的交易信息。当然,size()还可以用于移除长或短的交易记录!下一步,使用inspect()函数检查交易记录。因为上面识别出来的长交易记录将会导入非常长的输入,因此,我们来仅看2003年的前五个交易!
> inspect(Epub2003[1:5])
items transactionID TimeStamp
1 {doc_154} session_4795 2003-01-02 09:59:00
2 {doc_3d6} session_4797 2003-01-02 20:46:01
3 {doc_16f} session_479a 2003-01-02 23:50:38
4 {doc_11d,
doc_1a7,
doc_f4} session_47b7 2003-01-03 07:55:50
5 {doc_83} session_47bb 2003-01-03 10:27:44
大多数的交易记录只包含一项,只有交易4包含了3项。进一步查看(以列表的方式)
> as(Epub2003[1:5], "list")
$session_4795
[1] "doc_154"
$session_4797
[1] "doc_3d6"
$session_479a
[1] "doc_16f"
$session_47b7
[1] "doc_11d" "doc_1a7" "doc_f4"
$session_47bb
[1] "doc_83"
最后,使用coercion,水平布局的交易数据可以被转化成垂直布局的交易ID列表
> EpubTidLists <- as(Epub, "tidLists")
> EpubTidLists
tidLists in sparse format with
936 items/itemsets (rows) and
15729 transactions (columns)
处于性能的原因,交易ID列表也可以被存储在一个稀疏矩阵中。如下:
$doc_11d
[1] "session_47b7" "session_47c2" "session_47d8"
[4] "session_4855" "session_488d" "session_4898"
[7] "session_489b" "session_489c" "session_48a1"
[10] "session_4897" "session_48a0" "session_489d"
[13] "session_48a5" "session_489a" "session_4896"
[16] "session_48aa" "session_48d0" "session_49de"
[19] "session_4b35" "session_4bac" "session_4c54"
[22] "session_4c9a" "session_4d8c" "session_4de5"
[25] "session_4e89" "session_5071" "session_5134"
[28] "session_51e6" "session_5227" "session_522a"
[31] "session_5265" "session_52e0" "session_52ea"
[34] "session_53e1" "session_5522" "session_558a"
[37] "session_558b" "session_5714" "session_5739"
[40] "session_57c5" "session_5813" "session_5861"
[43] "session_wu48452" "session_5955" "session_595a"
[46] "session_5aaa" "session_5acd" "session_5b5f"
[49] "session_5bfc" "session_5f3d" "session_5f42"
[52] "session_5f69" "session_5fcf" "session_6044"
[55] "session_6053" "session_6081" "session_61b5"
[58] "session_635b" "session_64b4" "session_64e4"
[61] "session_65d2" "session_67d1" "session_6824"
[64] "session_68c4" "session_68f8" "session_6b2c"
[67] "session_6c95" "session_6e19" "session_6eab"
[70] "session_6ff8" "session_718e" "session_71c1"
[73] "session_72d6" "session_7303" "session_73d0"
[76] "session_782d" "session_7856" "session_7864"
[79] "session_7a9b" "session_7b24" "session_7bf9"
[82] "session_7cf2" "session_7d5d" "session_7dae"
[85] "session_819b" "session_8329" "session_834d"
[88] "session_84d7" "session_85b0" "session_861b"
[91] "session_867f" "session_8688" "session_86bb"
[94] "session_86ee" "session_8730" "session_8764"
[97] "session_87a9" "session_880a" "session_8853"
[100] "session_88b0" "session_8986" "session_8a08"
[103] "session_8a73" "session_8a87" "session_8aad"
[106] "session_8ae2" "session_8db4" "session_8e1f"
[109] "session_wu53a42" "session_8fad" "session_8fd3"
[112] "session_9083" "session_90d8" "session_9128"
[115] "session_9145" "session_916e" "session_9170"
[118] "session_919e" "session_91df" "session_9226"
[121] "session_9333" "session_9376" "session_937e"
[124] "session_94d5" "session_9539" "session_9678"
[127] "session_96a0" "session_9745" "session_97b3"
[130] "session_985b" "session_9873" "session_9881"
[133] "session_9994" "session_9a20" "session_9a2f"
[136] "session_wu54edf" "session_9af9" "session_9b69"
[139] "session_9ba4" "session_9c27" "session_9c99"
[142] "session_9ce8" "session_9de3" "session_9e8a"
[145] "session_9ebc" "session_a051" "session_a16e"
[148] "session_a19f" "session_a229" "session_a24a"
[151] "session_a328" "session_a340" "session_a3ab"
[154] "session_a3ee" "session_a43a" "session_a4b2"
[157] "session_a515" "session_a528" "session_a555"
[160] "session_a5bb" "session_a62d" "session_a77a"
[163] "session_ab9c" "session_abe9" "session_ac0e"
[166] "session_ad30" "session_adc9" "session_af06"
[169] "session_af4a" "session_af8d" "session_b0b7"
[172] "session_b391" "session_b6d3" "session_b807"
[175] "session_b8c7" "session_b91f" "session_bb0b"
[178] "session_bb8a" "session_bc3d" "session_bc40"
[181] "session_bceb" "session_bea7" "session_bf9f"
[184] "session_c359" "session_c3c2" "session_c442"
[187] "session_c62d" "session_c6ba" "session_c936"
[190] "session_ca81" "session_cad3" "session_cbd4"
[193] "session_cbe1" "session_cd63" "session_d14f"
[196] "session_d370" "session_d69f" "session_d815"
[199] "session_d82e" "session_d849" "session_d8b5"
[202] "session_da68" "session_db51" "session_db75"
[205] "session_dbcd" "session_dde2" "session_deac"
[208] "session_dfb7" "session_dfe9" "session_e00a"
[211] "session_e2ad" "session_e3c7" "session_e7d2"
[214] "session_e7e5" "session_e7f2" "session_ea38"
[217] "session_edbc" "session_edf9" "session_edfc"
[220] "session_f0be" "session_f2d9" "session_f2fe"
[223] "session_f39b" "session_f5e9" "session_f650"
[226] "session_f853" "session_f989" "session_fab1"
[229] "session_fcef" "session_fd0e" "session_fe49"
[232] "session_fe4f" "session_ffa0" "session_10057"
[235] "session_1019a" "session_1028a" "session_10499"
[238] "session_10513" "session_105e3" "session_10b03"
[241] "session_10b53" "session_10c0c" "session_10cb2"
[244] "session_10e4d" "session_10e67" "session_10e92"
[247] "session_10fbd" "session_10fcc" "session_114f1"
[250] "session_116fb" "session_11822" "session_1185e"
[253] "session_118d0" "session_11b0d" "session_12182"
[256] "session_121af" "session_121ee" "session_12405"
[259] "session_126db" "session_12825" "session_12896"
[262] "session_12a0b" "session_12c7c" "session_12e21"
[265] "session_1346d" "session_13622" "session_13886"
[268] "session_13d33" "session_140bd" "session_14428"
[271] "session_14b8a" "session_14e58" "session_14fdc"
[274] "session_1517f" "session_151b2" "session_15549"
[277] "session_155a9" "session_1571b" "session_15b18"
[280] "session_15b99" "session_15d2c" "session_15e0c"
[283] "session_15f75" "session_15fbf" "session_16621"
[286] "session_16691" "session_16f0d" "session_17027"
[289] "session_173fe" "session_17eaf" "session_17ecd"
[292] "session_180dd" "session_18641" "session_187ae"
[295] "session_18a0b" "session_18b18" "session_18db4"
[298] "session_19048" "session_19051" "session_19510"
[301] "session_19788" "session_197ee" "session_19c04"
[304] "session_19c7a" "session_19f0c" "session_1a557"
[307] "session_1ac3c" "session_1b733" "session_1b76a"
[310] "session_1b76b" "session_1ba83" "session_1c0a6"
[313] "session_1c11c" "session_1c304" "session_1c4c3"
[316] "session_1cea1" "session_1cfb9" "session_1db2a"
[319] "session_1db96" "session_1dbea" "session_1dc94"
[322] "session_1e361" "session_1e36e" "session_1e91e"
[325] "session_wu6bf8f" "session_1f3a8" "session_1f56c"
[328] "session_1f61e" "session_1f831" "session_1fced"
[331] "session_1fd39" "session_wu6c9e5" "session_20074"
[334] "session_2019f" "session_201a1" "session_209f9"
[337] "session_20e87" "session_2105b" "session_212a2"
[340] "session_2143b" "session_wu6decf" "session_218ca"
[343] "session_21bea" "session_21bfd" "session_223e1"
[346] "session_2248d" "session_22ae6" "session_2324d"
[349] "session_23636" "session_23912" "session_23a70"
[352] "session_23b0d" "session_23c17" "session_240ea"
[355] "session_24256" "session_24484"
$doc_13d
[1] "session_4809" "session_5dbc" "session_8e0b" "session_cf4b"
[5] "session_d92a" "session_102bb" "session_10e9f" "session_11344"
[9] "session_11ca4" "session_12dc9" "session_155b5" "session_1b563"
[13] "session_1c411" "session_1f384" "session_22e97"
$doc_14c
[1] "session_53fb" "session_564b" "session_5697" "session_56e2"
[5] "session_630b" "session_6e80" "session_6f7c" "session_7c8a"
[9] "session_8903" "session_890c" "session_89d2" "session_907e"
[13] "session_98b4" "session_c268" "session_c302" "session_cb86"
[17] "session_d70a" "session_d854" "session_e4c7" "session_f220"
[21] "session_fd57" "session_fe31" "session_10278" "session_115b0"
[25] "session_11baa" "session_11e26" "session_12185" "session_1414b"
[29] "session_14dba" "session_14e47" "session_15738" "session_15a38"
[33] "session_16305" "session_17b35" "session_19af2" "session_1d074"
[37] "session_1fcc4" "session_2272e" "session_23a3e"
在这个表达式中,每一项都有一个条目/元素(entry:即所有发生的交易记录组成的一个向量)。TidLists可以直接作为挖掘算法的输入(使用垂直数据库布局来挖掘关联规则!)
在下一节中,将会介绍如何创建一个数据集,以及如何挖掘规则!
#######例子2:准备和挖掘已给调查问卷数据集
第二个例子使用来自UCI机器学习库中的Adult数据集(arules包中有)。该数据集和市场篮子数据集类似,起源于美国人口普查数据库,包含了14个属性(年龄、工作类别、教育等)的48942个实例。该数据集之前是用这些属性来预测个人的收入水平。我们做了一些改变,将收入属性(attribute)设置成两个水平:small和large,分别代表收入小于50,000美元和大于50,000美元。
@ 加载数据集(AdultUCI)
> data("AdultUCI")
> dim(AdultUCI)
[1] 48842 15
> AdultUCI[1:2,]

AdultUCI包含了分类和指标属性的混合,在进行关联规则挖掘前,需要做一些准备工作。
@ 首先,移除两个属性:fnlwgt和education-num(一个代表体重,一个代表教育等级!)
> AdultUCI[["fnlwgt"]] <- NULL
> AdultUCI[["education-num"]] <- NULL
@ 然后,需要对剩下的四个度量属性(metric attributes:age、hours-per-week、capital-gain和capital-loss)通过建立合适的类别映射成顺序属性(ordinal attributes)!对于age和hours-per-week属性,使用了通用的年龄范围和工作时长划分。对于两个capital相关的属性,使用None代表have no gains/loss的情况(案例)。然后,继续group with gains/losses划分成两类Low和High!
> AdultUCI[[ "age"]] <- ordered(cut(AdultUCI[[ "age"]], c(15,25,45,65,100)),labels = c("Young", "Middle-aged", "Senior", "Old"))
> AdultUCI[[ "hours-per-week"]] <- ordered(cut(AdultUCI[[ "hours-per-week"]], c(0,25,40,60,168)),labels = c("Part-time", "Full-time", "Over-time", "Workaholic"))
> AdultUCI[[ "capital-gain"]] <- ordered(cut(AdultUCI[[ "capital-gain"]],c(-Inf,0,median(AdultUCI[[ "capital-gain"]][AdultUCI[[ "capital-gain"]]>0]),Inf)), labels = c("None", "Low", "High"))
> AdultUCI[[ "capital-loss"]] <- ordered(cut(AdultUCI[[ "capital-loss"]],c(-Inf,0,median(AdultUCI[[ "capital-loss"]][AdultUCI[[ "capital-loss"]]>0]),Inf)),
+ labels = c("none", "low", "high"))

@ 现在,现在这个数据就可以通过将其强转成transactions而被自动编码成一个二元发生矩阵(也叫关联矩阵:incidence matrix)!
> Adult <- as(AdultUCI, "transactions")
> Adult
transactions in sparse format with
48842 transactions (rows) and
115 items (columns)
剩下的115个分类属性被自动编码趁个15个二元项。项标签以<变量名>=<类别标签>的形式被生成!注:对于缺失值的cases(案例/行),对应该属性的所有项都会被设置为0
> summary(Adult)

这个结果的说明已在之前有所有描述,不记得的朋友请自行回顾!
@ 查看数据集中哪些项最重要,使用itemFrequencyPlot()函数,为了减少项的数量,我们只对支持度大于10%(使用参数support)的项回执项的频率(item frequency)。调整标签的大小,使用cex.names参数:
> itemFrequencyPlot(Adult, support = 0.1, cex.names=0.8)

Figure 6: Item frequencies of items in the Adult data set with support greater than 10%.
@ 现在,调用apriori函数发现所有规则(the default association type for apriori()) with a minimum support of 1% and a confidence of 0.6,这在前面也已经介绍啦哈!)
> rules <- apriori(Adult,parameter = list(support = 0.01, confidence = 0.6))

> rules
set of 276443 rules
简要解读一下这个结果:首先,输出了算法使用的参数。除了指定的最小支持度和最小置信度(minimum support and minimum confidence),所有的参数都有默认值!注意maxlen参数,挖掘出的最大频繁项集大小默认被限制为5,而长规则(long association rules)只在maxLen被设置成一个更高的值才被挖掘出来!这是需要注意的!||||在参数设置之后,输出的事算法控制和事件信息|||
@ 挖掘算法得到的是一个276443条规则的集合。使用summary函数查看挖掘规则概览.
> summary(rules)

可以看到,输出了规则的数量、包含在LHS和RHS中的最频繁项以及他们各自的长度分布、挖掘算法得出的优质度量(quality measures:这里指的其实就是支持度、置信度、提升度三个指标)简要统计信息!
@ 通常,得到的关联规则数量之巨大,为了分析这些规则,可以使用subset函数。例如:针对规则中右边(LHS)中收入(income)变量的每一项(如高收入、低收入等)生成单独的子规则。同时,要求提升度度量指标超过1.2
> rulesIncomeSmall <- subset(rules, subset = rhs %in% "income=small" & lift > 1.2)
> rulesIncomeLarge <- subset(rules, subset = rhs %in% "income=large" & lift > 1.2)
现在,我们得到了低收入人群和高收入人群的规则集合,作为对比,我们查看两个集合中置信度最高的三个规则(使用sort()函数)
> inspect(head(sort(rulesIncomeSmall, by = "confidence"), n = 3))

inspect(head(sort(rulesIncomeLarge, by = "confidence"), n = 3))

From the rules we see that workers in the private sector working part-time or in the service industry tend to have a small income while persons with high capital gain who are born in the US tend to have a large income.
这个例子说明:使用subset函数和sort函数对规则进行选择排序,即便是规则很大,也是可以分析的!
@ 最后,挖掘到的规则可以被写入到磁盘,以便分享给其他运用使用。使用write函数,将规则保存成文本格式。
> getwd()
[1] "D:/tangyang/documents/Data Analysis Examples"
> write(rulesIncomeSmall, file = "data.csv", sep = ",", col.names = NA)
# 将一组规则保存到文件名为data.csv(以逗号分隔)的文件中!
@补充,另外,使用pmml包,可以将一组规则以PMML(predictive modeling markup language)格式保存,一种基于XML的使用了诸多数据挖掘工具的标准化表达形式!需要注意的事pmml包的依赖包XML包可能不是对所有的操作系统都可用!!!
> write.PMML(rulesIncomeSmall, file = "data.xml")
保存的数据可以轻松的被用来分享。同样项集(itemsets)也可以用write函数写入一个文件!
######例子3:加入一个新的相关测度(Extending arules with a new interest measure)
这个例子中,主要讲解一下,向arules中添加一个新的相关测度是多么的容易,这里的相关测度使用Omiecinski (2003)介绍的all-confidence,一个项集X的all-confidence(全置信度)定义为:

该度量有一个特点: ,这里的I是项,X是项集。这意味着所有产生自项集X的规则至少必须有一个通过项集的全置信度值给定的置信!Omiecinski (2003)指出:上述方程分母中的支持度必须来自单个项,因此可以被简化为
,这里的I是项,X是项集。这意味着所有产生自项集X的规则至少必须有一个通过项集的全置信度值给定的置信!Omiecinski (2003)指出:上述方程分母中的支持度必须来自单个项,因此可以被简化为 。为了获取计算全置信度的项集,我们使用Ecalt算法来挖掘Adult数据集中的频繁项集!
。为了获取计算全置信度的项集,我们使用Ecalt算法来挖掘Adult数据集中的频繁项集!
> fsets<-eclat(Adult,parameter = list(support=0.05),control = list(verbose=FALSE ))
))
对于全置信的分母,我们需要找到所有已挖掘的单个项(single items)和他们响应的支持度值。接下来,我们创建一个命名向量(其中,名称是项的列数和值是他们支持度!)
> items(fsets)
itemMatrix in sparse format with
8496 rows (elements/transactions) and
115 columns (items)
> size(items(fsets))
[1] 4 3 3 3 3 2 2 2 2 4 3 3 3 2 2 2 2 5 5 5 4 4 4 5 4
[26] 4 4 3 3 3 3 5 4 4 4 3 3 3 4 3 3 3 2 2 2 2 2 2 4 3
[51] 3 3 5 4 4 4 3 3 3 5 4 4 4 3 3 3 4 3 3 3 2 2 2 2 2
[76] 2 2 4 3 3 5 4 4 5 4 4 4 3 3 3 3 4 4 4 4 3 3 3 3 6
[101] 5 5 5 4 4 4 5 4 4 4 3 3 3 3 5 4 4 4 3 3 3 4 3 3 3
[126] 2 2 2 2 2 2 2 2 4 4 5 4 4 4 5 4 4 4 5 4 4 4 5 4 4
[151] 4 3 3 3 3 3 3 3 5 4 4 4 3 3 3 5 4 4 4 3 3 3 5 4 4
[176] 5 4 4 4 3 3 3 3 5 4 4 5 4 4 4 3 3 3 3 5 4 4 4 3 3
[201] 3 4 3 3 3 2 2 2 2 2 2 2 2 2 4 3 3 4 4 6 5 5 5 4 4
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
[8301] 4 4 3 3 3 3 3 6 5 5 5 4 4 4 5 4 4 4 3 3 3 3 5 4 4
[8326] 4 3 3 3 4 3 3 3 2 2 2 2 2 2 2 7 6 6 6 5 5 5 6 5 5
[8351] 5 4 4 4 4 6 5 5 5 4 4 4 5 4 4 4 3 3 3 3 3 6 5 5 5
[8376] 4 4 4 5 4 4 4 3 3 3 3 5 4 4 4 3 3 3 4 3 3 3 2 2 2
[8401] 2 2 2 6 5 5 5 4 4 4 5 4 4 4 3 3 3 3 5 4 4 4 3 3 3
[8426] 4 3 3 3 2 2 2 2 2 5 4 4 4 3 3 3 4 3 3 3 2 2 2 2 4
[8451] 3 3 3 2 2 2 3 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[8476] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
####查找出只有单个项(item)的transactions(记录)
> singleItems <- fsets[size(items(fsets)) == 1] > singleItems
set of 36 itemsets
##### 获取单个项对应的支持度列(Get the col numbers we have support for)
> quality(singleItems)
support
8461 0.95327792
8462 0.91738668
8463 0.89742435
8464 0.85504279
。。此处省略。。
8493 0.07907129
8494 0.06420703
8495 0.06187298
8496 0.05439990
> singleSupport <- quality(singleItems)$support #获取支持度列
####对支持度命名!
> items(singleItems)
itemMatrix in sparse format with
36 rows (elements/transactions) and
115 columns (items)
> LIST(items(singleItems))
[[1]]
[1] "capital-loss=None"
[[2]]
[1] "capital-gain=None"
[[3]]
[1] "native-country=United-States"
[[4]]
[1] "race=White"
………此处省略………
[[33]]
[1] "workclass=Self-emp-not-inc"
[[34]]
[1] "workclass=Local-gov"
[[35]]
[1] "occupation=Machine-op-inspct"
[[36]]
[1] "education=Masters"
> unlist(LIST(items(singleItems),decode = FALSE))
[1] 66 63 111 60 8 62 70 114 2 31 50 61 33 21 3 71 51 25 1
[20] 115 26 53 29 45 38 39 69 36 47 54 43 58 10 6 42 27
> head(singleSupport, n = 5)
66 63 111 60 8
0.9532779 0.9173867 0.8974243 0.8550428 0.6941976
#####现在可以使用方程2(上面给出的全置信公式)计算所有的项集的全置信啦!公式中的分母部分我们已经得到(即命名向量singleSupport),得到的结果添加到集合优质(set's quality)数据框中!
> itemsetList <- LIST(items(fsets), decode = FALSE)
> allConfidence <- quality(fsets)$support/sapply(itemsetList, function(x) max(singleSupport[as.character(x)]))
> quality(fsets) <- cbind(quality(fsets), allConfidence)
> fsets
set of 8496 itemsets
> quality(fsets)[1:10,]
support allConfidence
1 0.05345809 0.05607818
2 0.05697965 0.05977234
3 0.05548503 0.06048162
4 0.05053028 0.05300687
5 0.05583309 0.05856959
6 0.05972319 0.06265034
7 0.05798288 0.06320441
8 0.05243438 0.05842763
9 0.05900659 0.08499971
10 0.05139020 0.05390893
####现在新的quality measure就是项集集合的一部分啦!查看一下便知!
> summary(fsets)

既然已经新的度量已经加入到quality measure集合中啦,它就可以被用来处理集合。例如,下面查看包含了与教育(education)相关的一项的项集(使用部分匹配%pin%),并用all-confidence对其排序!(我们首先过滤掉长度为1的项集,因为根据定义(per definition),他们的全置信为1)。
> fsetsEducation <- subset(fsets, subset = items %pin% "education") ##这个部分匹配略屌啊!!!(pin是partial in的缩写)
> inspect(sort(fsetsEducation[size(fsetsEducation)>1],by = "allConfidence")[1:3])
items support allConfidence
1 {education=HS-grad,
hours-per-week=Full-time} 0.2090209 0.3572453
2 {education=HS-grad,
income=small} 0.1807051 0.3570388
3 {workclass=Private,
education=HS-grad} 0.2391794 0.3445408
最后,得到的结果显示:the item high school graduate (but no higher education) is highly associated with working full-time, a small income and working in the private sector!
忙活了大半天,就是说的这个啊!哈哈……其实,all-confidence已经和其他相关测度一并被arules包实现了,调用这些相关测度的函数时interestMeasure()。
######例子4:抽样
这个例子演示sampling,即抽样如何在arules中使用,为了方便,数据集还是用adult数据集!
@ 加载数据集
> data("Adult")
> Adult
transactions in sparse format with
48842 transactions (rows) and
115 items (columns)
为了计算一个合理的样本量 n,这里使用Zaki et al. (1997a)开发的公式。同时选择5%的最小置信度。选择10%作为支持度可接受的误差率epsilon,选择90作为置信水平(1-c)%
> supp <- 0.05
> epsilon <- 0.1
> c <- 0.1
> n <- -2 * log(c)/ (supp * epsilon^2)
> n
[1] 9210.34
可见:得到的样本量比原始数据库小很多很多。
@ 使用sample函数(replace=TRUE:重复抽样!)从数据库中生成一个大小为n的样本
> AdultSample <- sample(Adult, n, replace = TRUE)
> AdultSample
transactions in sparse format with
9210 transactions (rows) and
115 items (columns)
@ 可以使用项频率图(item frequency plot)比较样本和数据库(总体)。样本中的项频率用条形表示(bars),而原始数据库中的项频率用线条(lines)表示。同样,使用cex.names参数调整label的大小,增强可读性(readability)。
itemFrequencyPlot(AdultSample, population = Adult, support = supp, cex.names = 0.7,col.lab='red')

@ 另外,可以使用提升比率(lift=TRUE)来比较样本与总体。每一项的提升比率=P(i|sample)/P(i|population),其中概率通过项频率来估计。提升比为1,表示:items occur in the sample in the same proportion as in the population!提升比大于1表示that the item is over-represented in the sample and vice versa,这个很好理解,就不啰嗦啦。
> itemFrequencyPlot(AdultSample, population = Adult,support = supp, lift = TRUE,cex.names = 0.9,col='yellow')

可以看到,less frequent items(非频繁项)有很大的相对偏差(deviations)
@ 为了比较样本达到的speed-up(这个词,我暂且理解成由于样本抽样带来速度提升而引起的项集优化等blablabla…),这里使用Eclat算法来对样本和总体同时挖掘频繁项集,并比较各自挖掘所需的系统时间!
> time <- system.time(itemsets <- eclat(Adult,parameter = list(support = supp), control = list(verbose = FALSE)))
> time
user system elapsed
0.19 0.02 0.20
> timeSample <- system.time(itemsetsSample <- eclat(AdultSample,parameter = list(support = supp), control = list(verbose = FALSE)))
> timeSample
user system elapsed
0.04 0.00 0.04
这里大概解释一下system.time返回的几个参数的意思哈!表示的是语句执行的需要的CPU时间。因此,对样本进行挖掘而不是总体可以得到一个加速因子:
> # speed up
> time[1] / timeSample[1]
user.self
4.75
@ 为了评估从样本中挖掘到的项集的准确性,通常分析两个集合之间的difference(差距)
> itemsets
set of 8496 itemsets
> itemsetsSample
set of 8351 itemsets
可见,两个集合的项集大致相同。
@ 检查两个集合是否包含相似的项集,这里进行集合(sets)匹配,来看看:fraction of frequent itemsets found in the database were also found in the sample.
> match <- match(itemsets, itemsetsSample, nomatch = 0) # 可以看到,没有匹配的都令其值为0
> match
[1] 8 9 10 0 11 12 13 14 15 0 2 3 4 5 6 7 0 16 17
[20] 0 18 19 20 0 21 22 23 24 25 26 27 28 29 30 31 32 33 34
[39] 35 36 37 38 39 40 41 42 43 44 51 52 53 54 55 56 57 58 59
[58] 60 61 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79
[77] 80 82 83 84 0 86 87 88 89 90 91 92 93 94 95 0 0 0 96
[96] 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115
[115] 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134
> ## remove no matches
> sum(match>0) / length(itemsets)
[1] 0.9662194
匹配率居然如此之高! 使用样本挖掘几乎找到了所有的频繁项集。
@ 没有在样本中发现的频繁项集的支持度合在样本中的频繁项集的统计摘要(summary)如下:
> summary(quality(itemsets[which(!match)])$support)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.05004 0.05053 0.05100 0.05120 0.05159 0.05503
> summary(quality(itemsetsSample[-match])$support)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.05005 0.05049 0.05092 0.05128 0.05168 0.05527
这个说明:只有支持度与最小支持度很接近的项集才会被错误的遗漏或发现!
@ 对于在数据库和样本中发现的频繁项集,这里从错误率中计算准确性
> supportItemsets <- quality(itemsets[which(match > 0)])$support
> supportSample <- quality(itemsetsSample[match])$support
> accuracy <- 1 - abs(supportSample - supportItemsets) / supportItemsets
> summary(accuracy)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.8939 0.9628 0.9785 0.9738 0.9893 1.0000
结论:The summary shows that sampling resulted in finding the support of itemsets with high accuracy.(说白了,说了这么多就是在说这个,最后终于得证)。This small example illustrates that for extremely large databases or for application where mining time is important, sampling can be a powerful technique!
参考文献
Aggarwal CC, Procopiuc CM, Yu PS (2002). "Finding Localized Associations in Market
Basket Data." Knowledge and Data Engineering, 14(1), 51–62.
Agrawal R, Imielinski T, Swami A (1993). "Mining Association Rules between Sets of Items
in Large Databases." In Proceedings of the 1993 ACM SIGMOD International Conference
on Management of Data, pp. 207–216. ACM Press. URL http://doi.acm.org/10.1145/
170035.170072.
Agrawal R, Srikant R (1994). "Fast Algorithms for Mining Association Rules." In JB Bocca,
M Jarke, C Zaniolo (eds.), Proc. 20th Int. Conf. Very Large Data Bases, VLDB, pp. 487–
499. Morgan Kaufmann.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号