2023.1.9(Educational Codeforces Round 141 & NEERC2017)
A.Yet Another Tournament
Link
https://codeforces.com/contest/1783/problem/C
Statement
除了你以外有 \(n\) 个人,编号为 \(0 \to n - 1\) ,每个人有两个权值 \(a_i\) 和 \(b_i\),其中 \(a_i = i\) ,\(b_i\) 给定。现在你要同这 \(n\) 个人依据 \(a_i\) 的大小来排名(\(a_i\) 越大排名越靠前,你的排名等于 \(a_i\) 严格大于你的人的个数)。
你的 \(a_i\) 的大小等于 \(k\),且需要满足 \(b_{x_1} + b_{x_2} + \cdots + b_{x_k} \leq m\) (在 \(n\) 个人中选 \(k\) 个人,他们的 \(b_i\) 的和不大于一个给定的数 \(m\) ,此时的 \(k\) 就作为你的 \(a_i\) 的值)。
最小化你的最终排名。
Solution
假设你最终赢了 \(x\) 个人。不难发现 \(i < x\) 和 \(i > x\) 的人,无论你是否选择了他们,他们都不会影响你的最终排名。所以只有 \(i = x\) 的人会影响你的最终排名。那我们只需先最大化自己赢的人的个数,最终判断能否选第 \(x\) 个人即可。
Code
#include <bits/stdc++.h>
using namespace std;
int T, n, m;
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
freopen("in","r", stdin);
cin >> T;
while (T--) {
cin >> n >> m;
vector<int> a(n);
for (auto &x : a) cin >> x;
auto b = a;
sort(b.begin(), b.end());
int sum = 0, cnt = 0;
for (auto x : b) {
if (x + sum > m)
break;
sum += x;
++cnt;
}
if (cnt == 0) cout << n + 1 << endl;
else if (cnt == n) cout << 1 << endl;
else (sum + a[cnt] - b[cnt - 1] <= m) ? cout << n - cnt << endl : cout << n - cnt + 1 << endl;
}
return 0;
}
B.Consonant Fencity
Link
Statement
定义以下集合:
给定字符串 \(s\), 函数 \(E(s)\) 等于「 \(s\) 中相邻字母均是 \(T\) 中的元素且大小写形式互不相同」的相邻对数。现在你可以改变任意字母在 \(s\) 中出现的大小写形式,但 \(s\) 中不同位置的本质相同的字母的形式均要相同,修改过后最终的字符串称作 \(s'\) 。最大化 \(E(s')\) 并输出 \(s'\) 。
Solution
考虑到 \(|T| = 19\),因此可以用一个二进制串来表示每一位(\(T\) 中每一种字母)的大小写形式,\(e.g. \ T_i = 1\) 表示大小,\(vice \ versa\).)
提前统计好 \(s\) 中出现过的 “\(T\) 元素对” 的个数,按题意统计即可。
Code
#include <bits/stdc++.h>
const int N = 100;
const char a[] = {'a', 'e', 'i', 'o', 'u', 'w', 'y'};
const char b[] = {'b', 'c', 'd', 'f', 'g', 'h', 'j', 'k', 'l', 'm', 'n', 'p', 'q', 'r', 's', 't', 'v', 'x', 'z'};
using namespace std;
string s;
bool con[N], vis[N];
int num[N][N];
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
freopen("consonant.in", "r", stdin);
freopen("consonant.out", "w", stdout);
cin >> s;
for (int i = 0; i < 7; i++) con[a[i] - 'a'] = true;
for (int i = 0; i < s.length() - 1; i++) {
if (!(con[s[i] - 'a'] & con[s[i + 1] - 'a'])) {
num[s[i] - 'a'][s[i + 1] - 'a']++;
num[s[i + 1] - 'a'][s[i] - 'a']++;
}
}
int ans = 0, maxx = 0;
for (int sta = 0; sta < (1 << 19); sta++) {
int res = 0;
for (int i = 0; i < 19; i++) {
if ((sta >> i) & 1) {
for (int j = 0; j < 19; j++) {
if (!((sta >> j) & 1)) res += num[b[i] - 'a'][b[j] - 'a'];
}
}
}
if (res > maxx) {
maxx = res;
ans = sta;
}
}
for (int i = 0; i < 19; i++) vis[b[i] - 'a'] = ((ans >> i) & 1);
for (int i = 0; i < s.length(); i++) vis[s[i] - 'a'] ? cout << (char)toupper(s[i]) : cout << s[i];
return 0;
}
C.Intelligence in Perpendicularia
Link
Statement
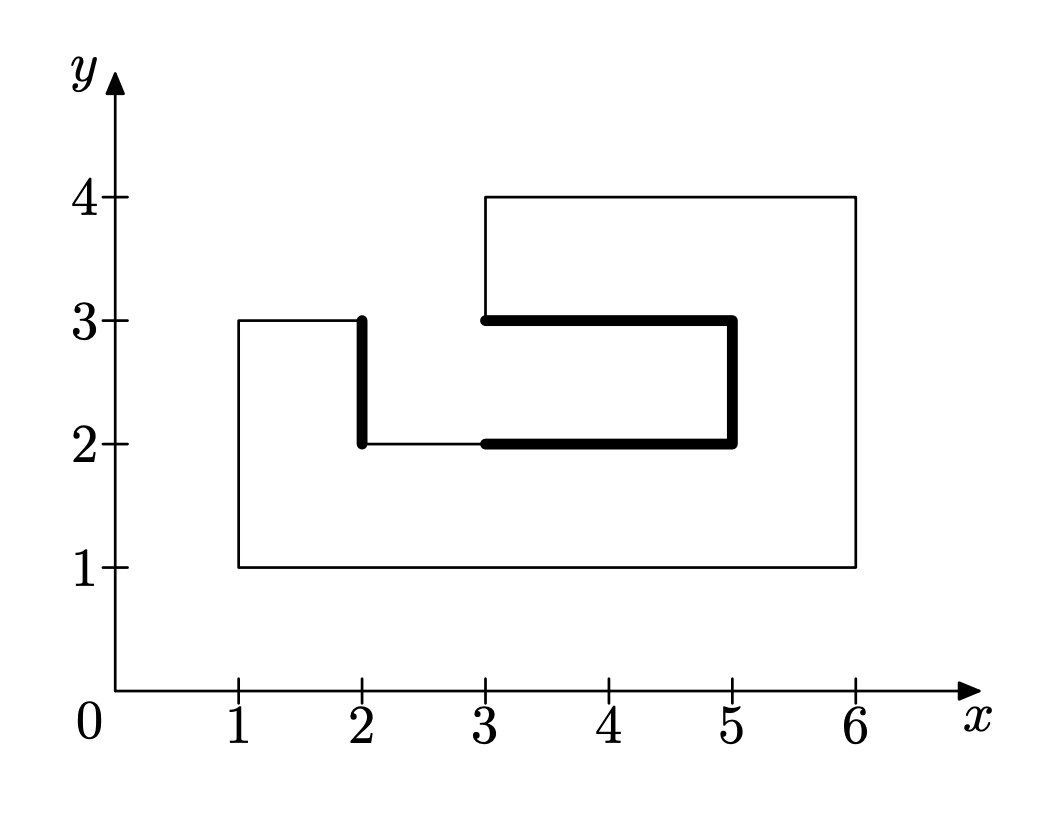
在一个平面直角坐标系中 \((-10 ^ 6 \leq x, y \leq 10 ^ 6)\) 描绘一个封闭图形,该图形的每条边均与 \(x\) 轴或 \(y\) 轴平行,现在沿 \(x\) 轴正、负方向,\(y\) 轴正、负方向(四个方向)“发射阳光”,问“照不到阳光”的线段的总长度。
上图中答案为 6。
Solution
由于坐标的范围不大,因此可以使用坐标的值当作下标,记录每个 \(x\) 或 \(y\) 经过的次数,不难发现只有经过次数大于 \(2\) 的线段才“照不到阳光”,且可以随着经过次数的增大被重复统计。
整个过程用差分的思想即可,即分别对 \(x\) 和 \(y\) 进行差分,最终统计累加即可。
Code
#include <bits/stdc++.h>
const int lim = 1e6 + 1;
typedef long long ll;
using namespace std;
int n, x[lim + 5], y[lim + 5];
ll dx[2 * lim + 5], dy[2 * lim + 5];
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
freopen("intel.in", "r", stdin);
freopen("intel.out", "w", stdout);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> x[i] >> y[i];
x[i] += lim;
y[i] += lim;
}
x[n + 1] = x[1], y[n + 1] = y[1];
for (int i = 2; i <= n + 1; i++) {
if (x[i] == x[i - 1]) {
int sy = min(y[i], y[i - 1]), ey = max(y[i], y[i - 1]);
dy[sy]++;
dy[ey]--;
}
else {
int sx = min(x[i], x[i - 1]), ex = max(x[i], x[i - 1]);
dx[sx]++;
dx[ex]--;
}
}
ll ans = 0;
for (int i = 1; i <= lim * 2 - 1; i++) {
dx[i] += dx[i - 1];
dy[i] += dy[i - 1];
ans += max(0ll, dx[i] - 2);
ans += max(0ll, dy[i] - 2);
}
cout << ans << endl;
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号