尺寸标注的文字应该绘制在哪里？

问题引入

在标注尺寸时，我们会在双向箭头中心处的旁边，绘制对应的文本提示。要绘制的文字位置看起来自然舒服，文本的绘制位置并不是简单地从线段中心点偏移固定值。

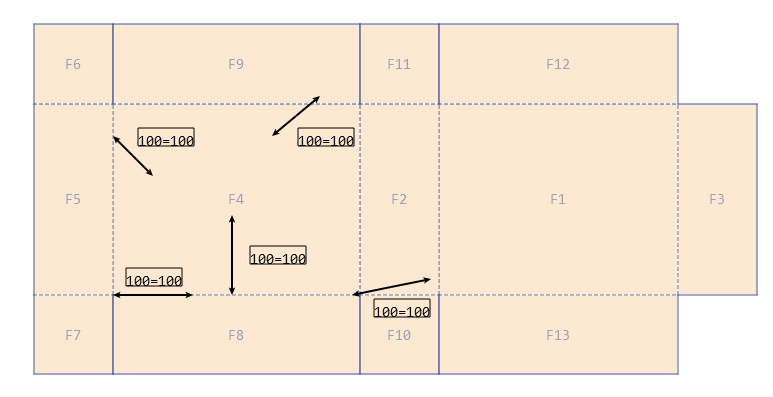
计算过程分析

 这里，提供一种计算标注文本位置的计算方式。

    

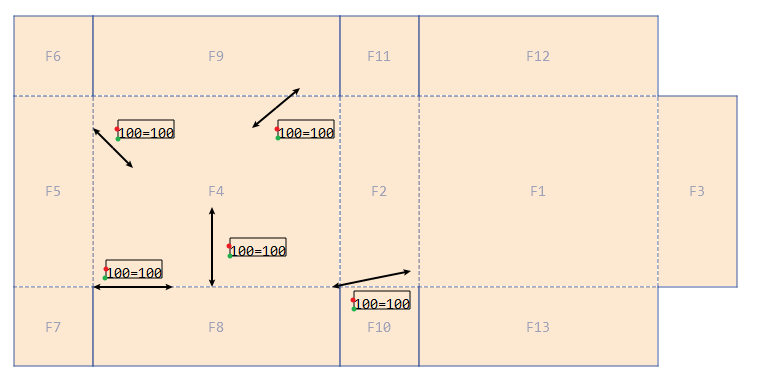
 如上图，绿色的点是文本位置的起点，经观察发现，文本左侧中心点相对于线段中心点的位置遵循一定的规律：

 

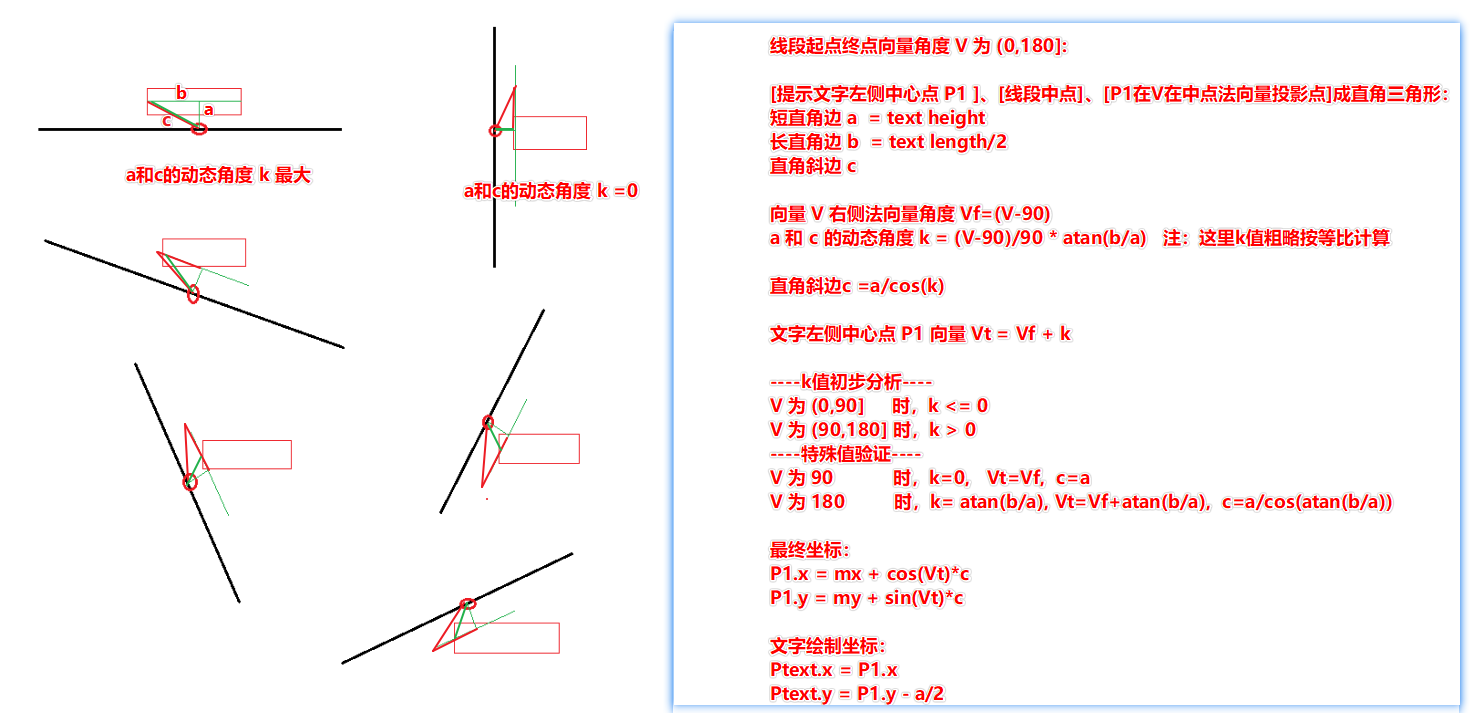
 线段起点终点向量角度 V 为 (0,180]:  

[提示文字左侧中心点 P1 ]、[线段中点]、[P1在V在中点法向量投影点]成直角三角形：  
短直角边 a  = text height
长直角边 b  = text length/2  
直角斜边 c                             

向量 V 右侧法向量角度 Vf=(V-90) 

（由于 V 的取值范围是 (0,180]，所以 Vf 的取值范围是 (-90,90] ）
a 和 c 的动态角度 k = (V-90)/90 * atan(b/a)   注：这里k值粗略按等比计算

（Vf=90度时，k=atan(b/a) ；Vf=0度时，k=0。这里根据这个按比例估算 k 的值，所以 90等分atan(b/a)）

直角斜边c =a/cos(k)

文字左侧中心点 P1 向量 Vt = Vf + k

----k值初步分析----
V 为 (0,90]     时，k <= 0
V 为 (90,180] 时，k > 0
----特殊值验证----
V 为 90           时，k=0,   Vt=Vf,  c=a
V 为 180         时，k= atan(b/a), Vt=Vf+atan(b/a),  c=a/cos(atan(b/a))

最终坐标：
P1.x = mx + cos(Vt)*c
P1.y = my + sin(Vt)*c

文字绘制坐标：
Ptext.x = P1.x
Ptext.y = P1.y - a/2

代码实现（参考）

//计算绘制文本时相对于线段（x1,y1），（x2,y2）中点的偏移点
void calculateTextOffsetForMiddlePt(double x1, double y1, double x2, double y2, int textLength, int textHeight, int& ptOffsetX, int& ptOffsetY)
{
    /*
    线段起点终点向量角度 V 为 (0,180]:  

[提示文字左侧中心点 P1 ]、[线段中点]、[P1在V在中点法向量投影点]成直角三角形：  
短直角边 a  = text height
长直角边 b  = text length/2  
直角斜边 c                             

向量 V 右侧法向量角度 Vf=(V-90)
a 和 c 的动态角度 k = (V-90)/90 * atan(b/a)   注：这里k值粗略按等比计算

直角斜边c =a/cos(k)

文字左侧中心点 P1 向量 Vt = Vf + k

----k值初步分析----
V 为 (0,90]     时，k <= 0
V 为 (90,180] 时，k > 0
----特殊值验证----
V 为 90           时，k=0,   Vt=Vf,  c=a
V 为 180         时，k= atan(b/a), Vt=Vf+atan(b/a),  c=a/cos(atan(b/a))

最终坐标：
P1.x = mx + cos(Vt)*c
P1.y = my + sin(Vt)*c

文字绘制坐标：
Ptext.x = P1.x 
Ptext.y = P1.y - a/2
    
    */

    //特殊情况
    if (ZMath_IsEqual(x1, x2) && ZMath_IsEqual(y1, y2))
        x2 -= 1.0; //重合时，把 （x1,y1），（x2,y2） 作为 180度线段来计算

    //确保:线段起点终点向量角度 V 为(0, 180]:
    double V = 0.0;
    ZMath_GetVectorAngle(x1, y1, x2, y2, &V);
    if (ZMath_IsEqual(V, 0.0) || (V > 180.0 && !ZMath_IsEqual(V, 180.0)))
        std::swap(x1, x2), std::swap(y1, y2);

    ZMath_GetVectorAngle(x1, y1, x2, y2, &V);

    double Vradian = ZMath_AngleToRadian(V);

    //短直角边 a  = text height ；长直角边 b = text length / 2
    double a = textHeight;
    double b = textLength / 2;

    //向量 V 右侧法向量角度 Vf=(V-90)
    double Vf = V - 90.0;
    double Vfradian = ZMath_AngleToRadian(Vf);

    //a 和 c 的动态角度 k = (V-90)/90 * atan(b/a)   注：这里k值粗略按等比计算
    double k = (V - 90) / 90 * atan(b / a);

    //直角斜边c =a/cos(k)
    double c = a / cos(k);

    //文字左侧中心点 P1 向量 Vt = Vf + k
    double Vtarget = Vfradian + k;

    //最终坐标：
    //P1.x = mx + cos(Vt)*c
    //P1.y = my + sin(Vt)*c
    //所以偏移值为
    double offsetX = cos(Vtarget) * c;
    double offsetY = sin(Vtarget) * c * -1; /* 绘制时是以左上角为原点，向上Y为负，向下Y为正，所以这里 Y 值乘以 -1 */

    //文字绘制坐标：
    //Ptext.x = P1.x 
    //Ptext.y = P1.y - a/2
    ptOffsetX = (int)offsetX;
    ptOffsetY = (int)(offsetY + a / 2); /* 绘制时是以左上角为原点，向上Y为负，向下Y为正，所以这里 Y 值加上 a/2 */
}

上述代码中：

ZMath_IsEqual 为判断两个浮点数是否相等，精度为 0.01

ZMath_GetVectorAngle 为获得线段的向量角度

ZMath_AngleToRadian 为角度转弧度

 

---

 

本文地址：https://www.cnblogs.com/BensonLaur/p/16916827.html