已知 [目标速度] 、 [加速时间] 和 [加加速度(Jerk)]，求运动过程的最大加速度

---

 一、问题引入 : 关于加加速度(Jerk)

理想情况下，让一个物体从静止运动起来时，在已知 [目标速度](V) 和 [加速时间](t) 的情况下，我们可以轻易地根据以下公式算出这个运动过程的加速度(a)

加速度计算公式：

(1)

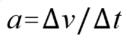
 所以，让静止物体在 [加速时间](t) 下达到 [目标速度](V) 的加速度为

 (2)

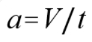
 然而，实际上现实生活中的运动，比如让机床机械轴动起来，不可能一下子瞬间就达到一个恒定的加速度，加速度是一直变化逐渐增加的到目标最大加速度的，显然我们无法直接使用公式 (2) 来准确描述这个运动过程的加速度。

在实际应用的场景中，我们需要一个更准确的运动描述模型，那就是加加速度(Jerk)

在运动控制领域，加加速度(Jerk) 是个很重要的概念，以下 倍福(Beckhoff) TwinCAT 提供的软件界面，可以提供给我们一个它的作用的参考：

 

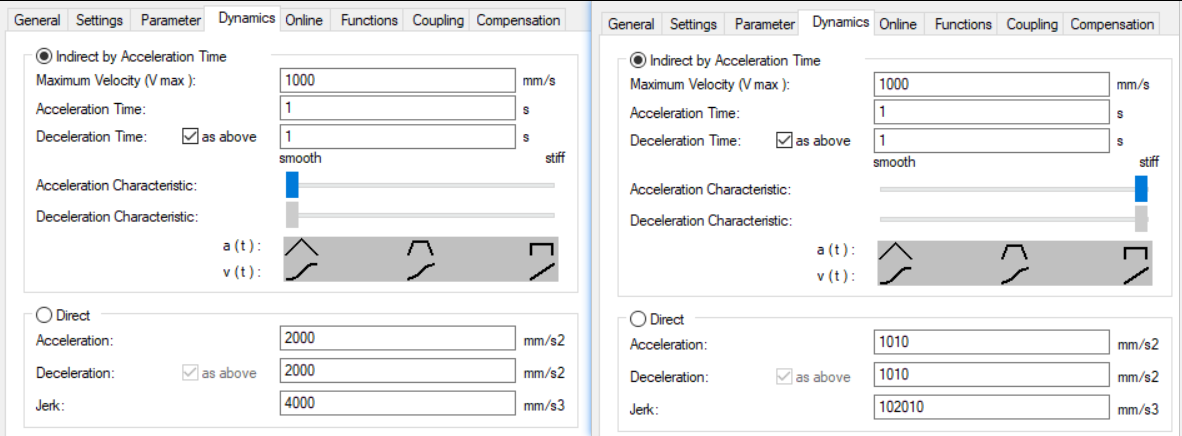
图一 倍福 TwinCAT System manager 轴参数设置页面

 

图中， Maxinum Velocity (V max) 为目标速度 V，

Acceleration Time 为整个过程加速所用的时间 t，

通过调整 Acceleration Characteristic 加速度特征 滑块，可以调整 加加速度(Jerk) ，

并得到运动过程对应的最大加速度 (为什么是最大加速度，刚刚有解释——现实运动加速度不是理想的固定值)。

---

二、运动过程分析

加速度是从 0 开始增加到最大加速度的，具体加速度随着时间的变化关系 a(t) 以及对应的速度随着时间变化关系 v(t) 示意如下：

 

 

 图二 a(t) 和 v(t)

 

如图二，最左边的 a(t) 和 v(t) 可以理解为在这个加速到最大速度 V 的过程中，加速度是不断在改变的，先是 “慢慢” 变到最大加速度 A，再立刻从最大加速度 A “慢慢” 降为 0

而图二中最右边的 a(t) 和 v(t) 可以理解为在这个加速到最大速度 V 的过程中，加速度在极短的时间内变大到最大加速度 A，然后在最大加速度下保持一定时间的，再在最后接近运动结束时快速降为0

这里，加速度本身变化的快慢，即是我们这里说的 加加速度(Jerk)

这整个过程可以分为三个阶段：

• （1）加速度从0开始增加阶段，用时 t0
• （2）加速度保持最大的阶段，用时 t1
• （3）加速度降低到0的阶段，用时也是 t0

整体用时 t = t0+t1+t0

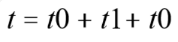
经过这三个阶段后，运动的速度从 0 增加到了目标速度 V

---

三、关系推导

回到这里的标题，已知 [目标速度] 、 [加速时间] 和 [加加速度(Jerk)]，如何求运动过程的最大加速度呢？

下面开始推导，令：

V = 目标速度

t = 加速时间

J = 加加速度（Jerk）

A = 运动过程中的最大加速度

则：

根据运动过程的三阶段，t0 ~ t1 ~ t0，可知

（1）

 加速度以加加速度 J 经过 t0 时间增加到了最大加速度 A，所以有

 （2）

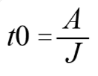
 将（2）代入（1）中，可得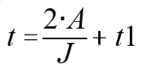：，即

（3）

 

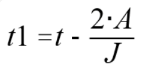
由于速度随着时间变化关系 v(t) 的导函数为 加速度随着时间的变化关系 a(t)，所以 a(t) 与 t 轴形成的面积即为速度的变化量 V

所以 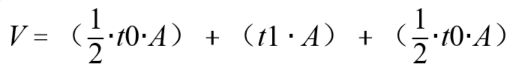，简化，得

 （4）

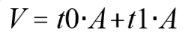
 将（2）代入（4）中去除 t0 ，可得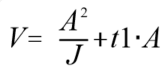，即有

（5）

 联立（3）（5），可得 ，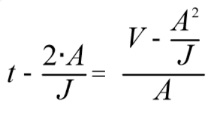

两边同时 x A，得 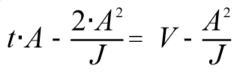，两边同时 x J，得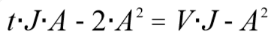 

 

 整理可得二元一次方程 ：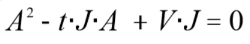

 解二元一次方程，可得 

 又由（2）式，可得 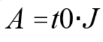 ，并且由（1）式可知 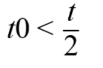，所以有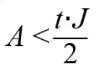 

 

 所以 A 只有一个解为：

 其中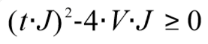，，即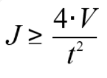

 

---

四、其它

本文公式使用的编辑器：https://math.edrawsoft.cn/

本文地址: https://www.cnblogs.com/BensonLaur/p/16835057.html