专题测试三 贪心与动态规划 B - Watering Grass

1. 题目
   n sprinklers are installed in a horizontal strip of grass l meters long and w meters wide. Each sprinkler
   is installed at the horizontal center line of the strip. For each sprinkler we are given its position as the
   distance from the left end of the center line and its radius of operation.
   What is the minimum number of sprinklers to turn on in order to water the entire strip of grass?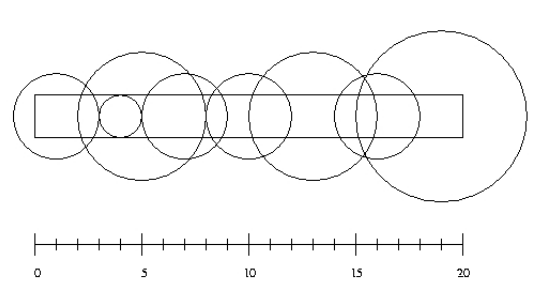
   
   Input
   Input consists of a number of cases. The first line for each case contains integer numbers n, l and w
   with n ≤ 10000. The next n lines contain two integers giving the position of a sprinkler and its radius
   of operation. (The picture above illustrates the first case from the sample input.)
   Output
   For each test case output the minimum number of sprinklers needed to water the entire strip of grass.
   If it is impossible to water the entire strip output ‘-1’.
   Sample Input
   8 20 2
   5 3
   4 1
   1 2
   7 2
   10 2
   13 3
   16 2
   19 4
   3 10 1
   3 5
   9 3
   6 1
   3 10 1
   5 3
   1 1
   9 1
   Sample Output
   6
   2
   -1
2. 思路
   一个圆里面，只有长方形与圆相交部分长度才是能完全覆盖的，把这部分长度算出来，就是实际能够覆盖的长度
   之后就是一个区间覆盖问题了，按左端点排序，每次选取现在覆盖区域内的左端点中，相对应的最远右端点
3. 代码
   

   #include<cstdio>
   #include<iostream>
   #include<string>
   #include<cstring>
   #include<algorithm>
   #include<cmath>
   using namespace std;
   
   #define clear(a) memset(a,0,sizeof(a))
   const int maxx = 10010;
   
   int N,ans,j=0;
   double L,W,start,endd,PO,R;
   
   struct Node{
       double s;
       double t;
   }p[maxx];
   
   bool cmp (Node a,Node b)
   {
   	return a.s < b.s;
   }
   
   void build(double point, double rr)
   {
   	double len;
   	if(rr < W/2) return;
   	else
   	{
   		len = sqrt(rr * rr - (W * W / 4));
   		p[j].s = point - len;
   		p[j].t = point + len;
   		j++;
   		return;
   	}
   }
   
   int main()
   {
   	while(scanf("%d%lf%lf",&N,&L,&W)!=EOF)
   	{
   		j = 0;
   		while(N--)
   		{
   			scanf("%lf%lf",&PO,&R);
   			build(PO,R);
   		}
   		sort(p,p+j,cmp);
   		start = 0;endd = 0; ans = 0;
   		bool flag = 0;
   		for (int i = 0; i < j; i++)
   		{
   			double s = p[i].s;
   			double t = p[i].t;
   			if (i == 0 && s > 0)
   				break;
   			if (s <= start) {
   				endd = max(t, endd);
   			}
   			else
   			{
   				ans++;
   				start = endd;
   				if (s <= start) {
   					endd = max(t, endd);
   				}
   				else
   				{
   					break;
   				}
   			}
   			if (endd >= L)
   			{
   				ans++;
   				flag = 1;
   				break;
   			}
   		}
   		if(flag) printf("%d\n", ans);
   		else printf("-1\n");
   	}
   }